Приклади визначення переміщень

Приклад 2.1.1 Для консольної балки, що навантажена силою 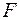та розподільним навантаженням 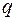на ділянці довжиною визначити вертикальне переміщення перерізу − .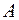

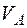Дано: 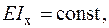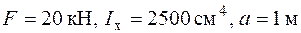. Визначаємо опорні реакції 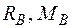(рис. 2.6 а).

Рисунок 2.6

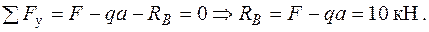
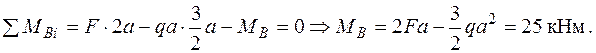
Навантажуємо балку одиничною силою у точці А (рис. 2.6 б), де треба визначити переміщення і визначаємо опорні реакції .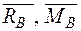

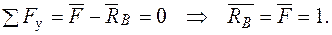
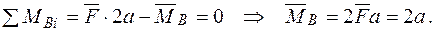
Записуємо рівняння згинальних моментів на ділянках балки від зовнішніх навантажень 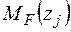і одиничного навантаження .

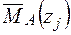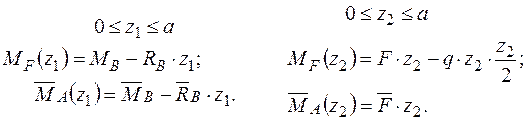
Визначаємо вертикальне переміщення перерізу 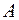− 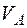двома способами. По-перше, застосуємо інтеграл Максвелла – Мора:

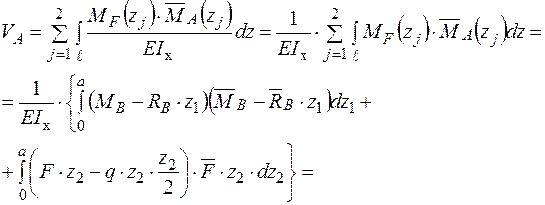
Додатне значення прогину 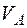зазначає, що переріз 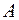переміщується в напрямку дії одиничного зусилля .

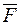По-друге, для визначення прогину в перерізі А застосуємо графоаналітичний спосіб. Для цього необхідно мати епюри згинального моменту від зовнішнього (рис. 2.6 в) та одиничного (рис. 2.6 г) навантажень. На ділянці, де − квадратична парабола, необхідно використовувати правило Симпсона – Корноухова (2.6), а на ділянці з лінійною залежністю – правило трапецій (2.5):

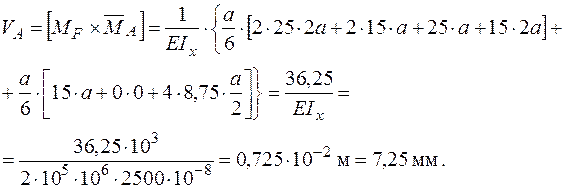
Двома методами отримано однакові результати, тому у наступних прикладах використовуємо графоаналітичний спосіб Верещагіна.

Дата добавления: 2014-12-26