
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Канонічні рівняння методу сил
|
|
|
|
Додаткові рівняння переміщень, що виражають рівність нулю переміщень (лінійних або кутових) у напрямках зайвих невідомих, зручно складати в так званій канонічній формі, тобто за певною закономірністю.
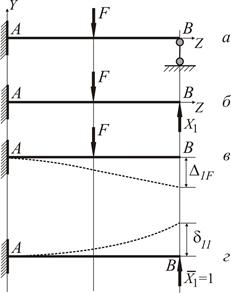
| Спочатку розглянемо систему, один раз статично невизначувану (рис. 2.17 а). Як зайве невідоме виберемо реакцію в опорі В. Тоді, навантаживши основну систему заданим навантаженням і зайвою невідомою силою 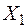 (еквівалентна система − рис. 2.17 б), прирівняємо до нуля повне переміщення точки В основної системи в напрямі (еквівалентна система − рис. 2.17 б), прирівняємо до нуля повне переміщення точки В основної системи в напрямі 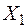 : :
|
Рисунок 2.17
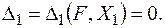 (2.7)
(2.7)
Обчислюючи 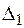 , застосуємо принцип незалежності дії сил:
, застосуємо принцип незалежності дії сил:
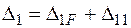 ,
,
де 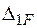 – переміщення від заданого навантаження (рис. 2.17 в);
– переміщення від заданого навантаження (рис. 2.17 в); 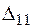 – переміщення від сили
– переміщення від сили 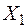 .
.
Якщо 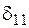 – переміщення в напрямі
– переміщення в напрямі 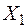 від сили
від сили 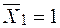 (рис. 2.17 г), то
(рис. 2.17 г), то 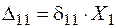 , і рівняння переміщень (2.7) набирає вигляду:
, і рівняння переміщень (2.7) набирає вигляду:
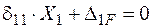 (2.8)
(2.8)
Це канонічна форма рівняння переміщень для один раз статично невизначуваної системи.
Для системи з двома зайвими зв’язками додаткові рівняння мають вигляд:  де
де  – повне переміщення в напрямі
– повне переміщення в напрямі 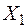 від заданого навантаження та зайвих невідомих сил
від заданого навантаження та зайвих невідомих сил 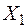 і
і  ;
; 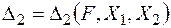 – повне переміщення в напрямі
– повне переміщення в напрямі  від заданого навантаження та зайвих невідомих сил
від заданого навантаження та зайвих невідомих сил 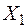 і
і  .
.
Виходячи з принципу незалежності дії сил, запишемо переміщення 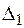 та
та  у вигляді сум переміщень, спричинених окремо кожною з невідомих сил
у вигляді сум переміщень, спричинених окремо кожною з невідомих сил 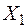 ,
,  та заданим навантаженням
та заданим навантаженням 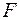 . Використовуючи вибрані раніше позначення переміщень, знаходимо:
. Використовуючи вибрані раніше позначення переміщень, знаходимо:
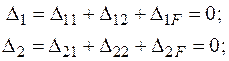
За аналогією можна записати в канонічній формі рівняння переміщень для будь-якої n разів статично невизначуваної системи:

Повне переміщення  можна визначити як добуток одиничного переміщення
можна визначити як добуток одиничного переміщення  , спричиненого дією одиничної сили
, спричиненого дією одиничної сили  , на відповідну узагальнену силу:
, на відповідну узагальнену силу: 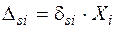 , тоді система рівнянь методу сил у канонічній формі набуває вигляду:
, тоді система рівнянь методу сил у канонічній формі набуває вигляду:
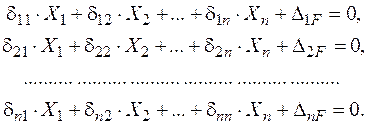 (2.9)
(2.9)
де 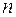 – кількість зайвих зв'язків (ступінь статичної невизначуваності) системи.
– кількість зайвих зв'язків (ступінь статичної невизначуваності) системи.
Коефіцієнти  рівнянь (2.9) являють собою лінійні зміщення або кути повороту в основній (статично визначуваній) системі від дії сил і моментів
рівнянь (2.9) являють собою лінійні зміщення або кути повороту в основній (статично визначуваній) системі від дії сил і моментів 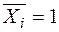 , доданих по напрямкам
, доданих по напрямкам 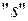 невідомих зусиль. Вільні члени
невідомих зусиль. Вільні члени  визначають відповідні узагальнені переміщення, викликані заданим зовнішнім навантаженням.
визначають відповідні узагальнені переміщення, викликані заданим зовнішнім навантаженням.
Коефіцієнти і вільні члени канонічних рівнянь (2.9) обчислюються за допомогою інтегралу Максвелла − Мора:
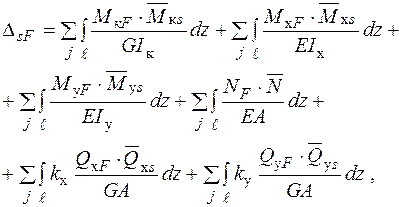 (2.10)
(2.10)
де складання проводиться по усім  дільницям пружної системи.
дільницям пружної системи.
Для визначення інтегралів Мора (2.10) необхідно мати відповідні епюри 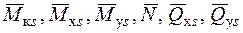 , які будують для основної системи, що навантажена тільки силами
, які будують для основної системи, що навантажена тільки силами  кожною окремо, а також «вантажні» епюри
кожною окремо, а також «вантажні» епюри  , які будують також для основної системи, але від заданого зовнішнього навантаження.
, які будують також для основної системи, але від заданого зовнішнього навантаження.
На відміну від просторової стержньової системи для багатопрольотної балки у виразі (2.10) залишаються складові, що містять згинальний момент та поперечну силу, а для плоскої рами − згинальний момент, поперечну і поздовжню сили.
В інженерних розрахунках реальних конструкцій дію поперечних та повздовжніх сил можна не враховувати, оскільки вони вносять незначний вклад у кінцевий результат. Тому вираз (2.10) набуває вигляд:
 . (2.11)
. (2.11)
Коефіцієнти канонічних рівнянь (2.9) визначають за формулою

На підставі теореми про взаємність переміщень 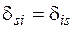 [1].
[1].
Значення коефіцієнтів канонічних рівнянь, як показують вирази (2.10), залежать від співвідношення згинальних  ,
,  та крутної
та крутної  жорсткостей поперечних перерізів стержньової системи та довжин
жорсткостей поперечних перерізів стержньової системи та довжин  відповідних ділянок стержня.
відповідних ділянок стержня.
Якщо рама зібрана з прямолінійних стержнів постійної згинальної і крутної жорсткості, то безпосереднє інтегрування в формулі Мора можна замінити перемноженням епюр по способу Верещагіна (2.3).
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 4092; Нарушение авторских прав?; Мы поможем в написании вашей работы!