
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Балки расчет балок с гибкой стенкой и ребрами
|
|
|
|
21.1 (18.2*). Расчетные формулы приведены для балок со стенками, подкрепленными поперечными ребрами жесткости, несущих статическую нагрузку, с относительной гибкостью стенки 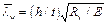 , находящейся в пределах от 6 до 13. Ограничение сверху сделано для предотвращения выпучивания в плоскости стенки сжатых поясов балки, выполняемых из листовой стали. Ограничение снизу указано ориентировочно, в связи с чем этим методом расчета можно пользоваться и при
, находящейся в пределах от 6 до 13. Ограничение сверху сделано для предотвращения выпучивания в плоскости стенки сжатых поясов балки, выполняемых из листовой стали. Ограничение снизу указано ориентировочно, в связи с чем этим методом расчета можно пользоваться и при 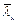 < 6, если проверка выполняется в соответствии с пп. 7.1, 7.2*, 7,3, 7.4* СНиП II-23-81*. Сущность применяемого метода состоит в учете закритической стадии работы стенки.
< 6, если проверка выполняется в соответствии с пп. 7.1, 7.2*, 7,3, 7.4* СНиП II-23-81*. Сущность применяемого метода состоит в учете закритической стадии работы стенки.
21.2 (18.2*). Наиболее полное решение для балки симметричного двутаврового сечения при чистом изгибе получено в работе [31]. Придельное значение момента Ми найдено из выражения, аппроксимирующего точное решение:
Ми /(WRy) = (y + 0,224 c)/(y + 0,224), (145)
где y = Af / Aw; c = 0,259 + 1,945/(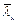 - 1,1).
- 1,1).
В табл. 63 приведены значения предельных моментов, вычисленные по формуле (145).
Таблица 63
| Значение y | Значения Ми /(WRy) при 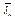 , равной , равной
| |||
| 0,5 | 0,858 | 0,838 | 0,826 | 0,817 |
| 1,0 | 0,916 | 0,904 | 0,897 | 0,892 |
| 2,0 | 0,954 | 0,947 | 0,943 | 0,940 |
Эпюры предельных мембранных напряжений sх [31] показывают, что в зоне растяжения эпюра близка к линейной, но краевое напряжение не достигает предела текучести. Для практических расчетов в СНиП II-23-81* принята упрощенная схема предельного состояния, в которой сжатая зона стенки представляет собой прямоугольник высотой h1 с напряжением, равным расчетному сопротивлению Ry (рис. 47). Краевое растягивающее напряжение также принято равным по абсолютной величине Ry. При малой толщине поясов по сравнению с высотой стенки и 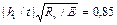 получена формула (159) СНиП II-23-81*, которая дает несколько преувеличенные (от 1 до 3,6 %) значения Ми, поскольку в действительной эпюре напряжений в растянутом поясе расчетное сопротивление не достигается.
получена формула (159) СНиП II-23-81*, которая дает несколько преувеличенные (от 1 до 3,6 %) значения Ми, поскольку в действительной эпюре напряжений в растянутом поясе расчетное сопротивление не достигается.
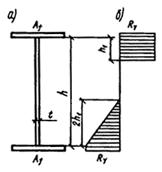
Рис. 47. Схема предельного состояния сечения балки при изгибе
а - сечение балки; б - эпюра напряжений
21.3 (18.2*). Поперечная сила Qu, воспринимаемая стенкой, слагается из двух частей: силы Qcr = tсрht, отвечающей критической нагрузке, и дополнительной силы D Q, возникающей в закритической стадии вследствие образования диагональной или близкой к ней растянутой полосы. Различные модели отличаются углом наклона и шириной этой полосы, а также значением предельного растягивающего напряжения (распределение напряжений обычно считается равномерным). В работе [32] принято, что ось полосы совпадает с диагональю (рис. 48), а ширина полосы определяется положением пластического шарнира, возникающего вследствие изгиба пояса. В сечение пояса включается полоса стенки шириной от 0 до 30 t в зависимости от tср / Ry. Предельное напряжение растяжения в диагональной полосе находится из условия, чти интенсивность напряжений равна пределу текучести.
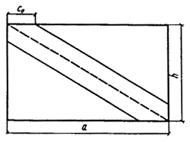
Рис. 48. Схема отсека стенки балки при сдвиге
Метод Рокки-Шкалоуда [32] можно существенно упростить посредством допущений, ведущих к некоторому уменьшению предельной нагрузки. Этот вариант реализован в СНиП II-23-81*.
Предельное касательное напряжение в стенке tu определяется из выражения
 , (146)
, (146)
где m = a / h;
tcr - критическое касательное напряжение;
co / a - определяется из формул:
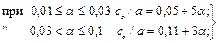 (147)
(147)
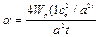 ;
;
Wp - пластический момент сопротивления сечения пояса, в который включается полоса стенки шириной 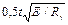 ; при вычислениях по формуле (162) СНиП II-23-81* для упругого тавра вместо Wp подставляется 2 Wmin.
; при вычислениях по формуле (162) СНиП II-23-81* для упругого тавра вместо Wp подставляется 2 Wmin.
Если в практических расчетах получается, что co / a > 0,4, то необходимо принимать co / a = 0,4. Значение tcr следует вычислять с учетом упругого защемления стенки в поясах, например, по формуле (76) СНиП II-23-81*. Из формулы (146) настоящего Пособия получена формула (160) СНиП II-23-81*.
21.4 (18.3). В описанной модели предельного состояния закритическая работа стенки обусловлена появлением диагональной растянутой полосы, следовательно, ребро должно выполнять роль сжатой стойки и воспринимать усилие D Q = (tu - tcr) ht.
В сечение ребра можно включить часть стенки по 0,65 t  с каждой стороны. При проверке прочности и устойчивости одностороннего ребра следует учитывать эксцентриситет сжимающей силы, равный расстоянию от срединной плоскости стенки до центра тяжести сечения ребра. Этот способ расчета приведен в СНиП II-23-81*.
с каждой стороны. При проверке прочности и устойчивости одностороннего ребра следует учитывать эксцентриситет сжимающей силы, равный расстоянию от срединной плоскости стенки до центра тяжести сечения ребра. Этот способ расчета приведен в СНиП II-23-81*.
21.5 (18.2). Комбинация изгиба со сдвигом теоретически рассмотрена с использованием обычных допущений (упругая пластинка, условные критерии предельного состояния). Кривая взаимодействия момента и поперечной силы близка к известной кривой для критических нагрузок. Истинная кривая должна быть более выпуклой, так как формы выпучивания от предельного момента и предельной поперечной силы, действующих порознь, различаются больше, чем соответствующие собственные функции линейных краевых задач.
Экспериментальная проверка выполнена на малом числе образцов, поэтому для практических расчетов обычно рекомендуются эмпирические кривые взаимодействия в координатах Q / Qu и М / Ми (символы без индексов относятся к комбинированному нагружению), в частности, формула (158) СНиП II-23-81*, дающая небольшой запас несущей способности.
21.6 (18.7*). Предельное значение сосредоточенной силы, приложенной к поясу (bftf) двутавровой тонкостенной балки, находится из условия, что наибольшее напряжение в стенке под грузом равно расчетному сопротивлению:
Fu = 3,26 tRy  ,
,
где 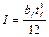 .
.
Тогда 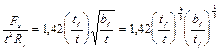 . (148)
. (148)
При передаче давления через полку двутавра, лежащего на балке, или через прокладку значение Fu можно увеличить на 10 %.
РАСЧЕТ БАЛОК С ГИБКОЙ НЕПОДКРЕПЛЕННОЙ СТЕНКОЙ (18.9*)
21.7. Рекомендации настоящего подраздела распространяются на расчет и проектирование сварных двутавровых балок из стали с пределом текучести до 430 МПа (4400 кгс/см2) со стенками, не укрепленными поперечными ребрами жесткости, за исключением опорных участков, и имеющими гибкость 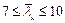 7.
7.
21.8. Расчет разрезных балок, нагруженных равномерно распределенной нагрузкой, следует выполнять в соответствии с требованиями разд. 18 СНиП II-23-81*.
Для получения равнопрочного поперечного сечения в пролетной и опорных зонах балки значения 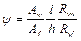 следует назначать в пределах 22 £ y £ 26.
следует назначать в пределах 22 £ y £ 26.
21.9. Прочность сечений балок, нагруженных неравномерной нагрузкой, следует проверять по формулам:
при М / Мu £ 0,5 Q / Qu £ 1;
” 0,5 < М / Ми < 1 (Q / Qu - 0,5)2 + (М / Ми - 0,5)2 £ 0,25;
” М / Ми = 1 Q / Qu £ 0,5,
где М и Q - соответственно момент и поперечная сила в рассматриваемом сечении балки;
Мu - предельный момент, вычисляемый по формуле
 (здесь l = hw / t);
(здесь l = hw / t);
Qu - предельная поперечная сила, H, вычисляемая по формуле
 , Ryw в МПа.
, Ryw в МПа.
21.10. При передаче нагрузки на верхний пояс следует предусматривать конструктивные мероприятия, исключающие появление эксцентриситета, превышающего половину толщины стенки.
21.11. Начальные прогибы стенки балок относительно вертикальной плоскости не должны превышать величины 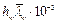 , см.
, см.
21.12. Заводской сварной стык стенки следует располагать на расстоянии не менее 3 hw от опорного ребра.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1850; Нарушение авторских прав?; Мы поможем в написании вашей работы!