Методические рекомендации. Вопросы, выносимые на обсуждение

Вопросы, выносимые на обсуждение

1. Определение определенного интеграла и его свойства.

2. Вычисление определенного интеграла с помощью формулы Ньютона-Лейбница.

3. Формула замены переменной в определенном интеграле.

4. Формула интегрирования по частям в определенном интеграле.

Для подготовки к занятию дома

1. Прочитайте конспект лекции, соответствующий теме занятия. Запомните основные определения.

2. Изучите рекомендуемую литературу по вопросам, выносимым на обсуждение.

3. Найдите ответы на теоретические задания для развития и контроля владения компетенциями. Подготовьтесь к ответам на эти вопросы на занятии.

4. Законспектируйте ответы на теоретические задания, которые не содержатся в Вашем конспекте лекции по указанной теме.

5. Изучите разобранные примеры решения типовых задач и законспектируйте их решение в рабочую тетрадь.

На занятии по указанию преподавателя

1. Дайте ответы на вопросы из теоретических заданий для развития и контроля владения компетенциями.

2. В рабочей тетради и на доске решите практические задания для развития и контроля владения компетенциями из заданий, решаемых в аудитории.

3. Пройдите компьютерное тестирование по данной теме.

Дома закрепите полученные практические умения и навыки, решая практические задания для развития и контроля владения компетенциями из заданий для самостоятельной работы дома.

Рекомендуемая литература

[1] глава 9 пп. 9.6 – 9.7.

[2] глава X § 1.

[3] глава 8 § 42.

[4] часть III занятия 10, 12.

[5] глава 5 §§ 5.1. – 5.4.

[6] глава 8 § 1, §§ 7 – 9.

[7] глава VIII § 1, §§ 7 – 9.

[8] глава 6 § 6, §§ 8 – 10.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

1. Применяя формулу Ньютона-Лейбница, вычислите определенный интеграл:

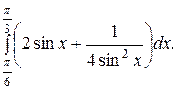
Решение. Для того, чтобы вычислить определенный интеграл по формуле Ньютона-Лейбница надо:

1) найти первообразную функции;

2) в полученную первообразную подставить вместо аргумента сначала верхний предел интегрирования, затем нижний предел интегрирования и из первого результата вычесть второй.

Исходя из этого, имеем:

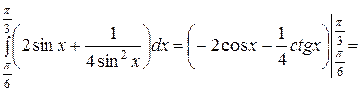
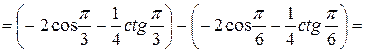
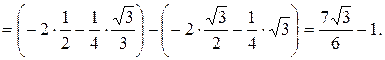
2. Вычислите определенные интегралы:

а) 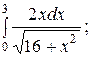б)

Решение. а) Этот интеграл вычисляется с помощью замены переменной. При замене пересчитываем пределы интегрирования:

.

б) Для вычисления этого интеграла воспользуемся формулой интегрирования по частям в определенном интеграле:

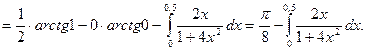
Интеграл 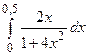вычисляем заменой переменой:

Отсюда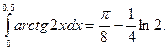

Теоретические задания

Дата добавления: 2014-12-26