
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Завдання для самостійної роботи
|
|
|
|
5.7. Розв’язати рівняння:
а) 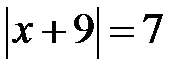 ; b)
; b) 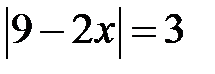 ; c)
; c) 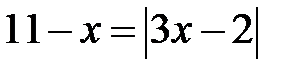 ; d)
; d) 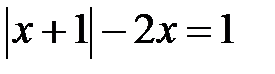 .
.
5.8. Розв’язати рівняння 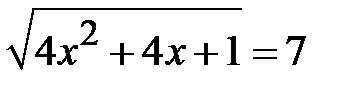 .
.
5.9. Зобразити на числовій осі точки, що задовольняють нерівності:
а) 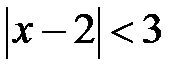 ; b)
; b) 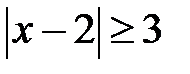 ; c)
; c) 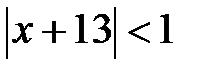 ; d)
; d) 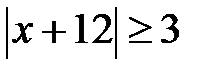 ; e)
; e) 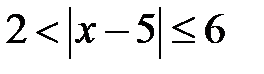 ; f)
; f) 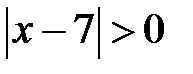 ;
;
g) 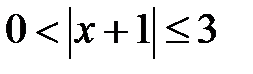 .
.
5.10. Визначити, для яких значень 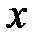 геометрична прогресія із знаменником
геометрична прогресія із знаменником 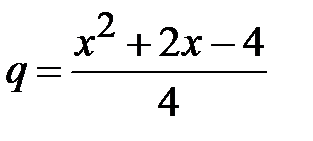 буде нескінченно спадною, тобто
буде нескінченно спадною, тобто 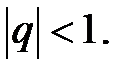
5.11. Розв’язати нерівності: а) 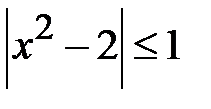 ; b)
; b) 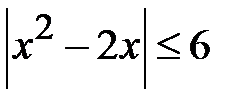 .
.
5.12. Розв’язати рівняння:
а) 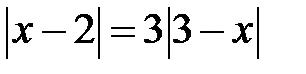 ; b)
; b) 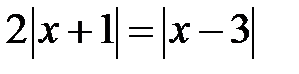 ; c)
; c) 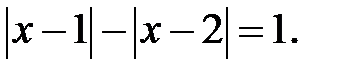
5.13. Розв’язати нерівності:
а)  ; b)
; b) 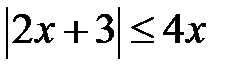 ; c)2
; c)2 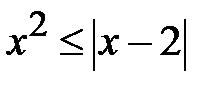 ; d)
; d) 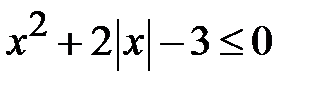 .
.
5.4. Показникові та логарифмічні рівняння
Рівняння, що містять невідому в показникові степеня, мають назву “показникові рівняння”.
Основні види показникових рівнянь такі:
1. 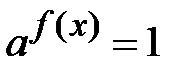
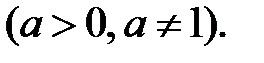
За визначенням нульового показника 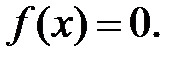
2. 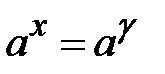
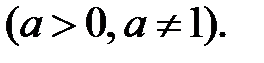
Якщо розділити обидві частини рівняння на 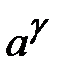
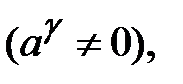 то одержимо рівняння
то одержимо рівняння 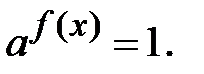
3. 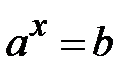
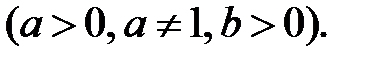
За означенням логарифма 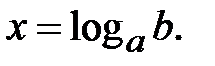
4. 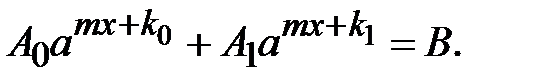
Винесемо за дужки 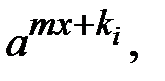 де
де 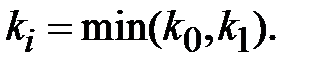 Маємо
Маємо
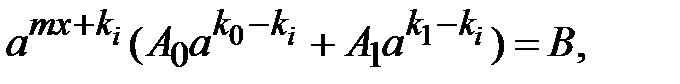 або
або 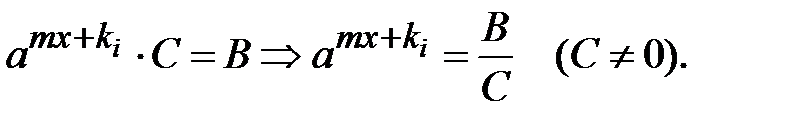
Рівняння має розв`язок, якщо 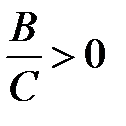 .
.
5. 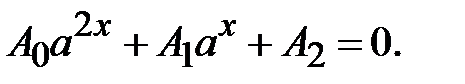
Позначимо 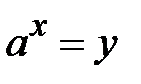 , тоді одержимо квадратне рівняння відносно
, тоді одержимо квадратне рівняння відносно 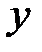 , оскільки
, оскільки 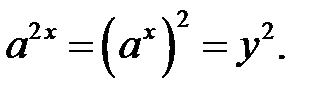
6. 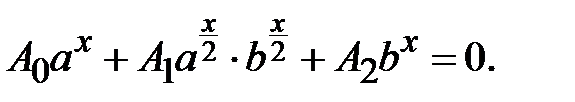
Поділивши обидві частини на 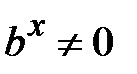 , отримаємо рівняння, що має вигляд рівняння 5.
, отримаємо рівняння, що має вигляд рівняння 5.
Приклад5.17. Розв’язати рівняння 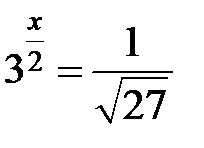 .
.
Розв’язання. Праву частину 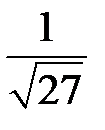 перетворимо в число з основою 3:
перетворимо в число з основою 3: 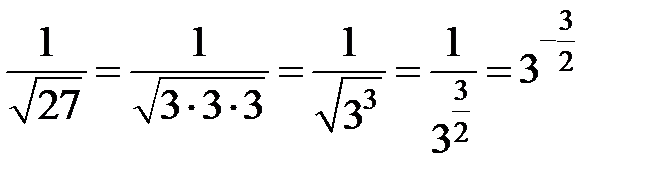 . Тепер підставимо
. Тепер підставимо 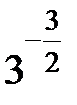 в рівняння. Маємо
в рівняння. Маємо 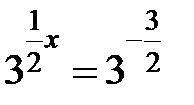 Þ
Þ 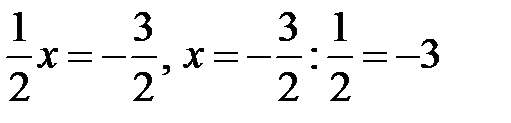 .
.
Приклад5.18. Розв’язати рівняння 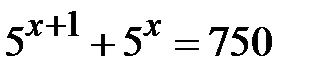 .
.
Розв’язання. Оскільки 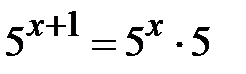 , то рівняння матиме вигляд
, то рівняння матиме вигляд 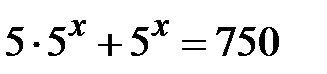 . Винесемо
. Винесемо 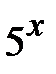 за дужки:
за дужки: 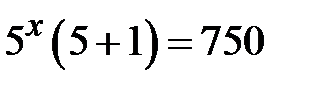 Þ
Þ 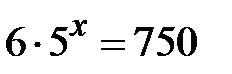 Þ
Þ 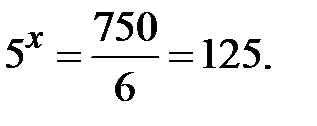 Таким чином,
Таким чином, 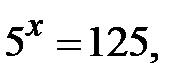 але
але 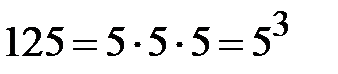 Þ
Þ 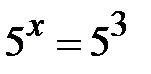 Þ
Þ 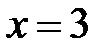 .
.
Приклад5.19. Розв’язати рівняння 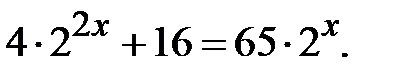
Розв’язання. Позначимо  , тоді
, тоді 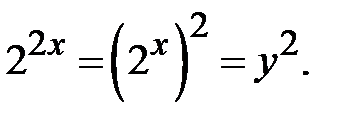 Підставимо
Підставимо 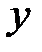 і
і 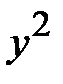 в задане рівняння. Отримаємо квадратне рівняння
в задане рівняння. Отримаємо квадратне рівняння 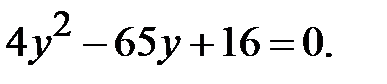 Розв’яжемо це рівняння. Маємо:
Розв’яжемо це рівняння. Маємо: 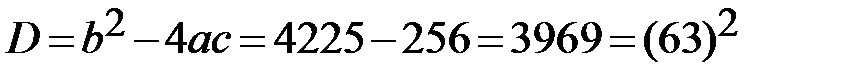 Þ
Þ 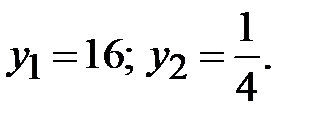 Звідси:
Звідси: 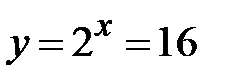 ,
, 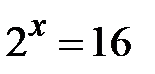 ,
, 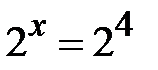 ,
, 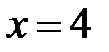 і
і  ,
, 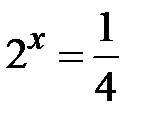 ,
, 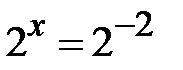 ,
, 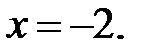
Приклад 5.20. Розв’язати рівняння 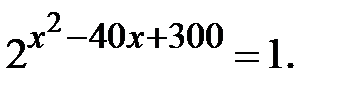
Розв’язання. 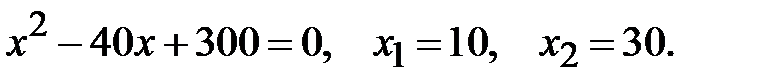
Приклад 5.21. Розв’язати рівняння 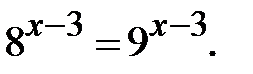
Розв’язання. 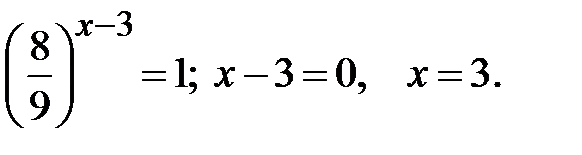
Приклад 5.22. Розв’язати рівняння 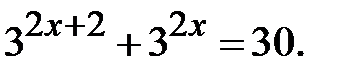
Розв’язання. Винесемо за дужки 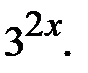 Отримаємо:
Отримаємо:
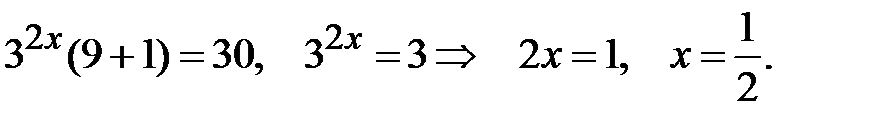
Приклад 5.23. Розв’язати рівняння 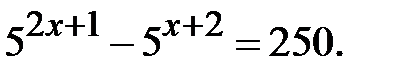
Розв’язання. Позначимо 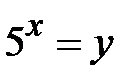 . Маємо
. Маємо 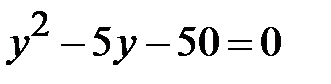 . Корені квадратного
. Корені квадратного
рівняння: 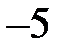 і
і 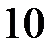 . Оскільки
. Оскільки 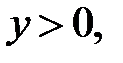 то нас влаштовує тільки корінь
то нас влаштовує тільки корінь 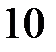 . Тоді
. Тоді 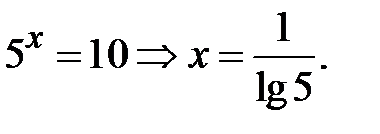
Якщо невідома змінна міститься під знаком логарифма або в його основі, то таке рівняння називається логарифмічним. При розв’язуванні логарифмічних рівнянь обов’язково потрібно враховувати властивості логарифмічної функції 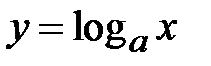 :
: 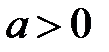 ,
, 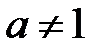 ,
, 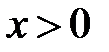 .
.
Приклад 5.24. Розв’язати рівняння 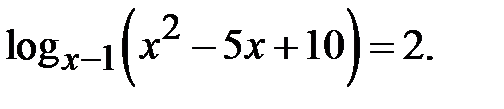
Розв’язання. Для цього рівняння ОДЗ таке: 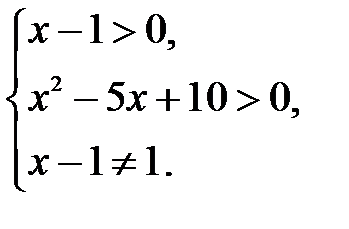
Розв’яжемо нерівність 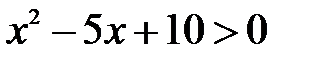 :
: 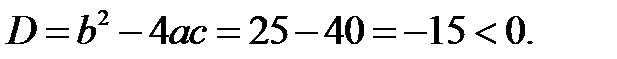 Парабола
Парабола 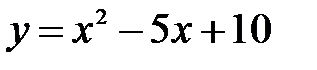 не має точок перетину з віссю
не має точок перетину з віссю 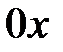 . Отже,
. Отже, 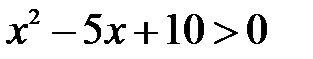 для будь-яких
для будь-яких 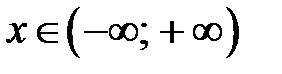 . Тоді
. Тоді 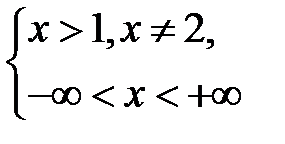 Þ
Þ 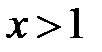 ,
, 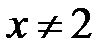 . За означенням логарифма
. За означенням логарифма 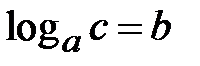 маємо
маємо
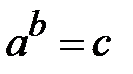 Þ
Þ 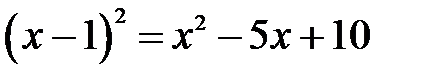 Þ
Þ 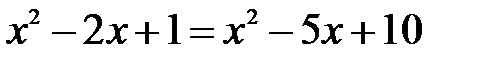 Þ
Þ 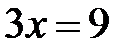 ,
, 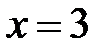 .
.
Приклад 5.25. Розв’язати рівняння 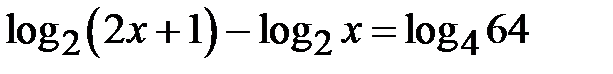 .
.
Розв’язання. Визначимо ОДЗ цього рівняння:  Þ
Þ 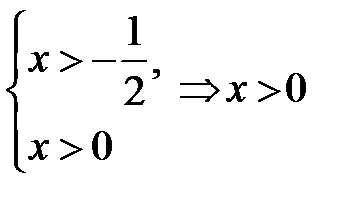 .
.
До лівої частини рівняння застосуємо властивість 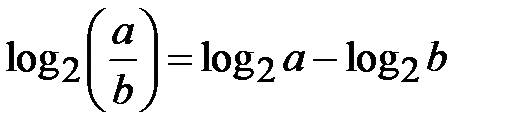 , тобто ліва частина дорівнює логарифму дробу
, тобто ліва частина дорівнює логарифму дробу 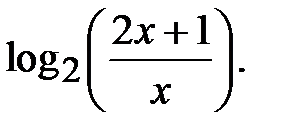 В правій частині рівняння
В правій частині рівняння 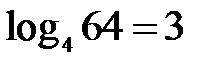 . Тоді початкове рівняння набуде вигляду
. Тоді початкове рівняння набуде вигляду 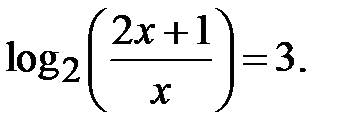 За означенням логарифма
За означенням логарифма 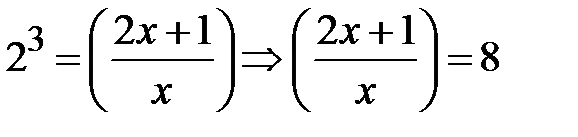 . Оскільки
. Оскільки 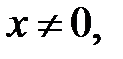 то
то 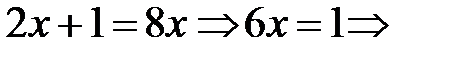
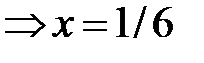 .
.
Приклад 5.26. Розв’язати рівняння 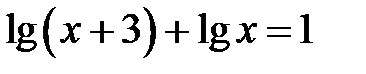 .
.
Розв’язання. Для цього рівняння ОДЗ таке: 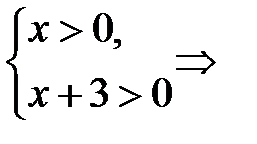
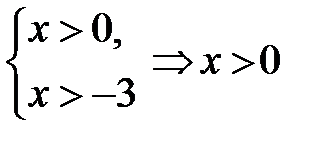 . До лівої частини рівняння застосуємо властивість
. До лівої частини рівняння застосуємо властивість 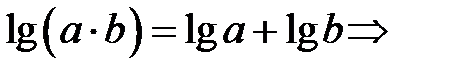
 . За означенням десяткового логарифма
. За означенням десяткового логарифма 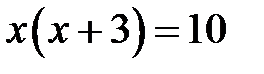 ,
, 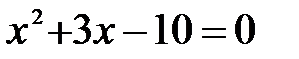 ,
, 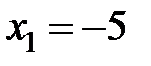 ,
, 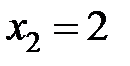 . Врахуємо, що
. Врахуємо, що 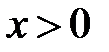 , тоді
, тоді 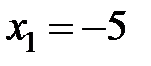 не є коренем цього рівняння.
не є коренем цього рівняння.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 422; Нарушение авторских прав?; Мы поможем в написании вашей работы!