
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Завдання для самостійної роботи. 5.18. Розв’язати найпростіші тригонометричні рівняння:
|
|
|
|
5.18. Розв’язати найпростіші тригонометричні рівняння:
а) 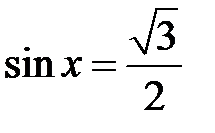 ; b)
; b) 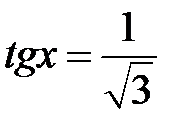 ; c)
; c) 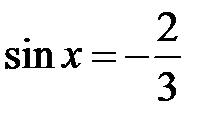 ; d)
; d) 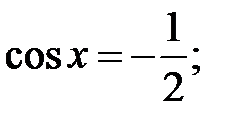
e) 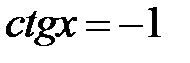 ; f)
; f) 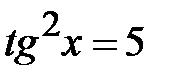 ; g)
; g) 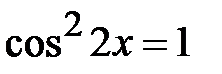 ; h)
; h) 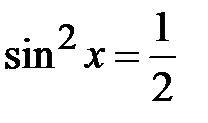 .
.
Розв’язки рівнянь зобразити на тригонометричному колі.
Розв’язати тригонометричні рівняння:
5.19. а) 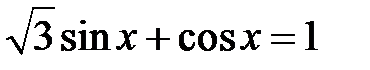 ; b)
; b) 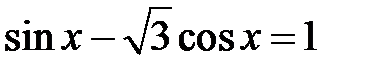 ; c)
; c) 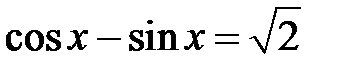 ;
;
d) 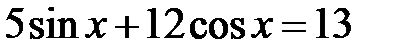 ; e)
; e) 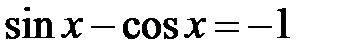 ; f)
; f) 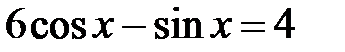 .
.
5.20. 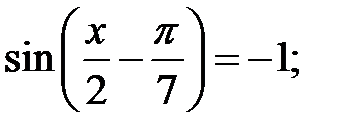 5.21.
5.21. 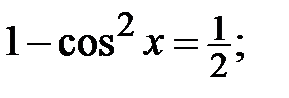 5.22.
5.22. 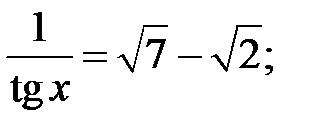
5.23. 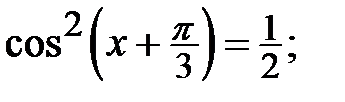 5.24.
5.24. 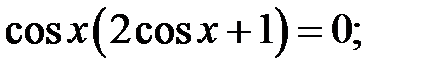 5.25.
5.25. 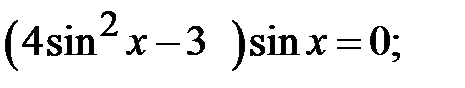
5.26. 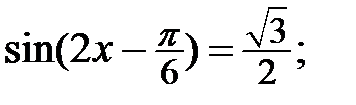 5.27.
5.27. 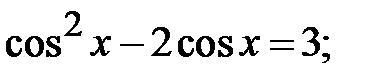 5.28.
5.28. 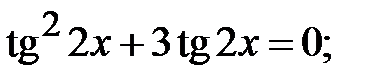
5.29. 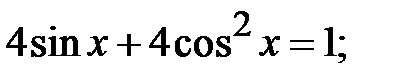 5.30.
5.30. 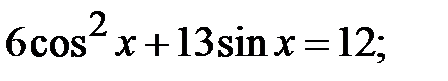 5.31.
5.31. 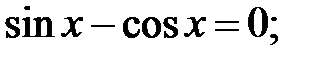
5.32. 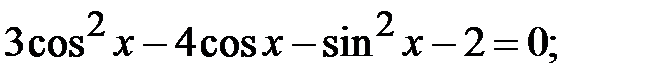 5.33.
5.33. 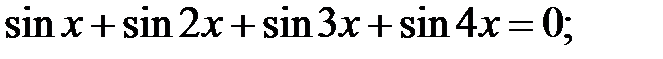
5.34. 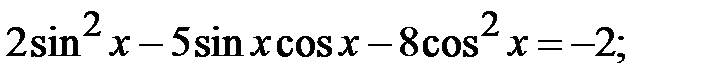 5.35.
5.35. 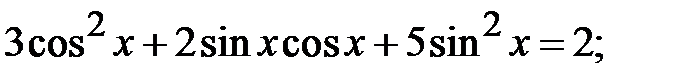
5.36.  5.37.
5.37. 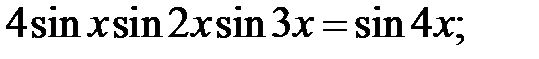
5.38. 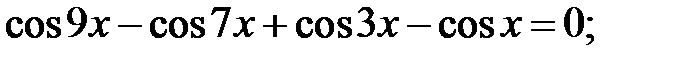 5.39.
5.39. 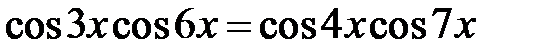 .
.
5.7 Тригонометричні нерівності
Розв’язання тригонометричних нерівностей зводиться, як правило, до розв’язання найпростіших тригонометричних нерівностей вигляду 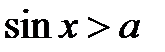 ,
, 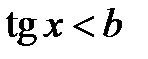 і
і
т. п., а також до розв’язання сукупностей або систем тригонометричних нерівностей. Для розв’язання найпростіших тригонометричних нерівностей зручно користуватися тригонометричним колом. Множина значень змінної величини, яка задовольняє дану найпростішу нерівність, зображується на тригонометричному колі у вигляді однієї або кількох дуг. При цьому зазначимо, що якщо точка кола відповідає числу  , то вона відповідає і всім числам вигляду
, то вона відповідає і всім числам вигляду 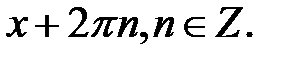
Приклад 5.40. Розв’язати нерівність 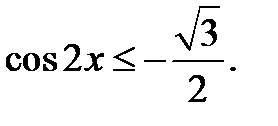
Розв’язання. За означенням 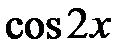 – це абсциса точки на тригонометричному колі (рис. 5.11), яка відповідає числу
– це абсциса точки на тригонометричному колі (рис. 5.11), яка відповідає числу 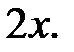 Відкладемо на колі точки, які мають абсциси, що дорівнюють (
Відкладемо на колі точки, які мають абсциси, що дорівнюють (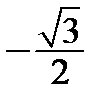 ). Це точки А
). Це точки А 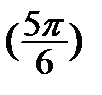 і B
і B 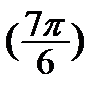 . Геометричним розв’язком наведеної нерівності буде замкнена дуга AmB тому, що
. Геометричним розв’язком наведеної нерівності буде замкнена дуга AmB тому, що
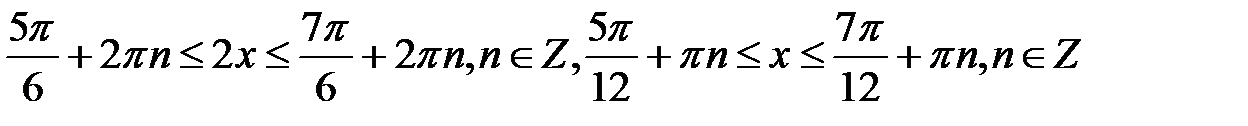 , або
, або
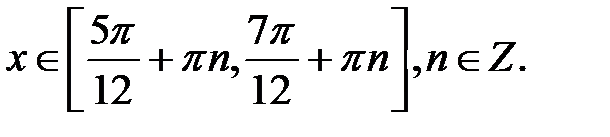
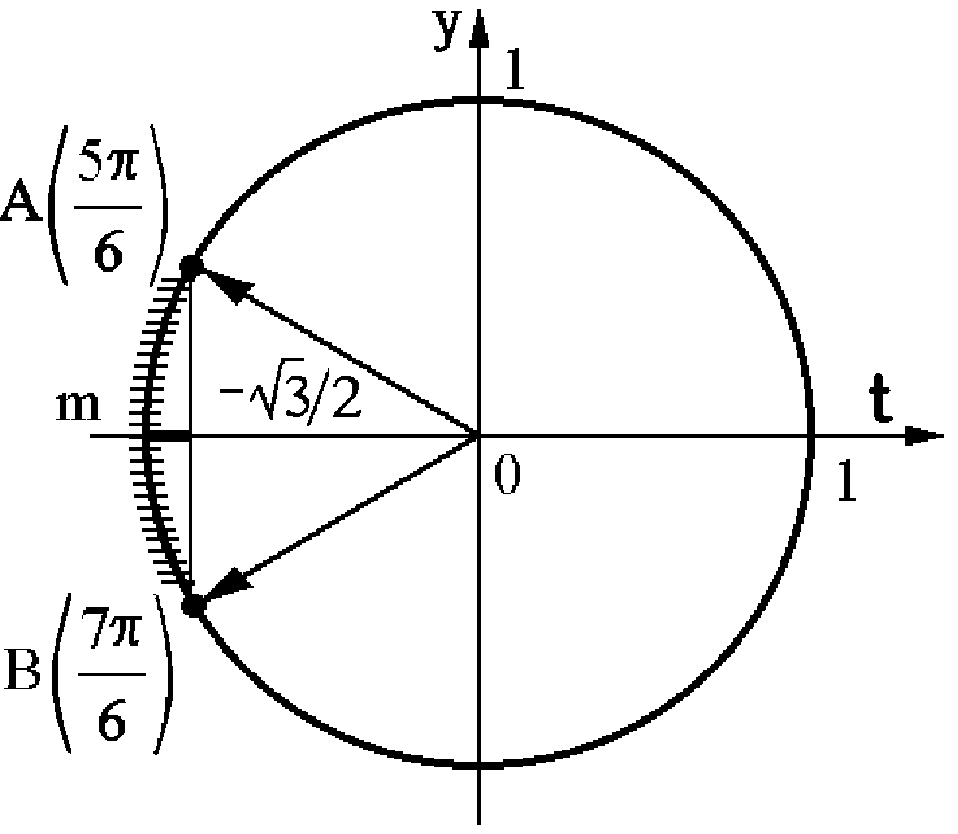 Рис. 5.11
Рис. 5.11
| 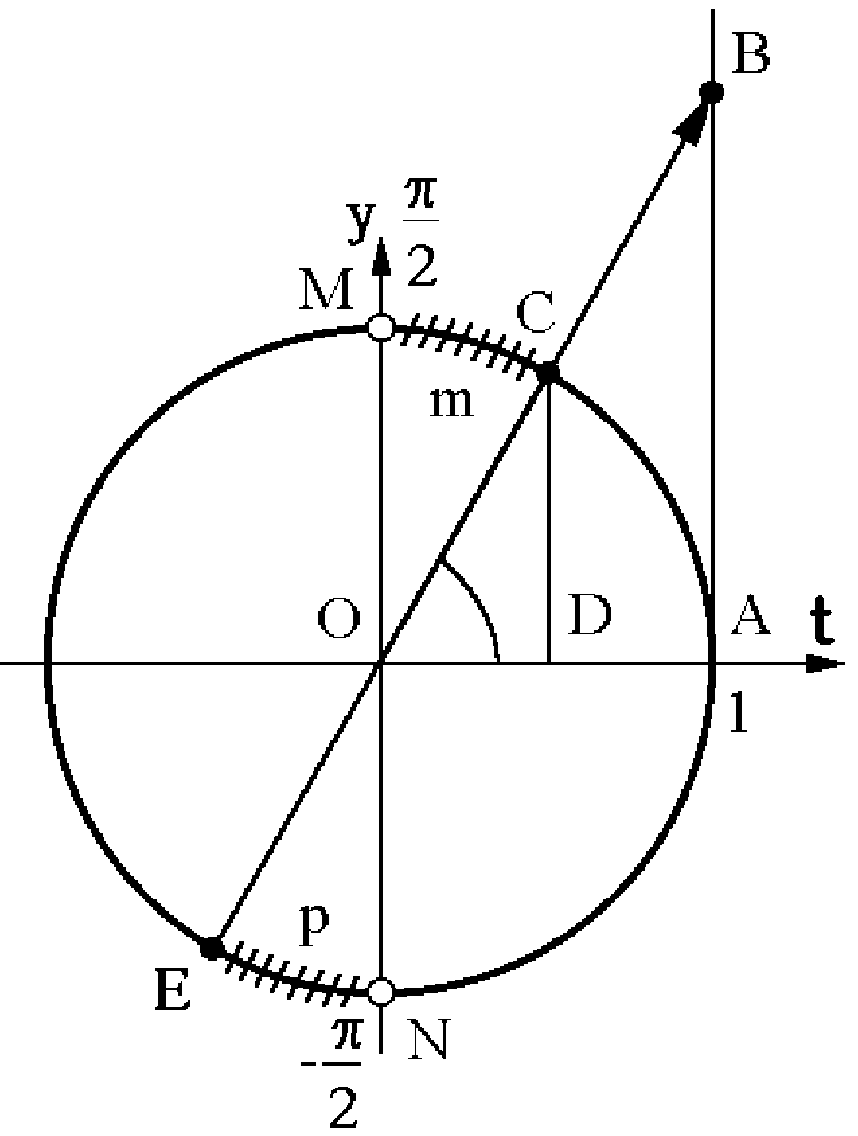 Рис. 5.12
Рис. 5.12
|
Приклад 5.41. Розв’язати нерівність 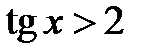 .
.
Розв’язання. Функція 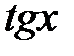 не визначена в точках
не визначена в точках 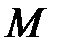 і
і 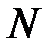 при
при 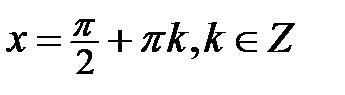 (рис. 5.12). Проведемо вісь тангенсів
(рис. 5.12). Проведемо вісь тангенсів 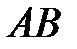 перпендикулярно до осі абсцис
перпендикулярно до осі абсцис 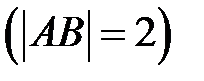 . Промінь
. Промінь 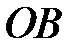 перетинає одиничне коло в точці С
перетинає одиничне коло в точці С 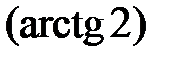 :
:
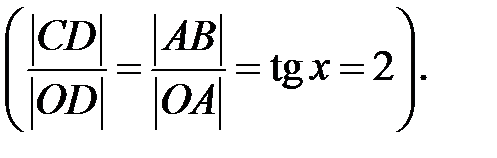
Функція 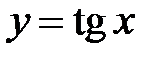 монотонно зростає при
монотонно зростає при 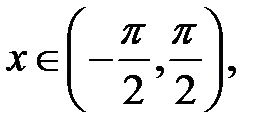 тому нерівність
тому нерівність  буде виконуватися для всіх точок відкритої дуги СmМ. Оскільки головний період функції
буде виконуватися для всіх точок відкритої дуги СmМ. Оскільки головний період функції 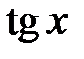 дорівнює
дорівнює  , то наведена нерівність буде виконуватися для всіх точок дуги ЕрN. Складемо аналітичний запис вказаних дуг:
, то наведена нерівність буде виконуватися для всіх точок дуги ЕрN. Складемо аналітичний запис вказаних дуг:
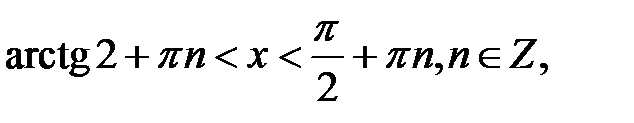
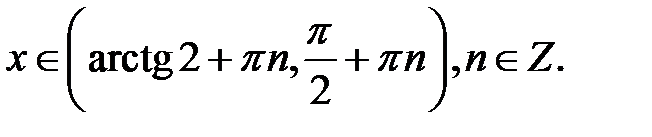
Приклад 5.42. Розв’язати нерівність 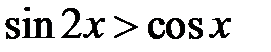 .
.
Розв’язання. Перепишемо нерівність у вигляді
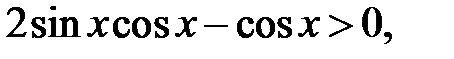
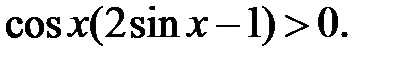
Остання нерівність рівносильна системам нерівностей
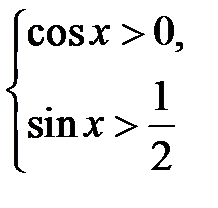 (1) і
(1) і 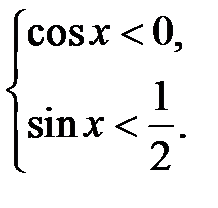 (2)
(2)
Геометричний розв’язок систем (1) і (2) подано на рис. 5.13 і 5.14 відповідно. Це будуть дуги AmC і FpM. Об’єднуючи ці дуги, запишемо аналітичний запис розв’язків:
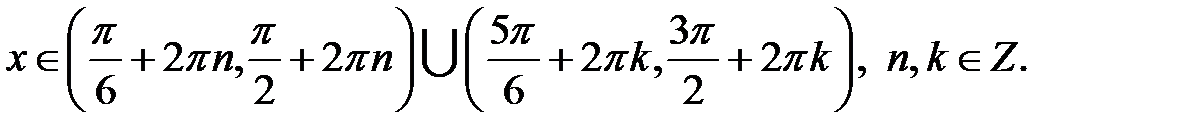
Приклад 5.43. Розв’язати нерівність 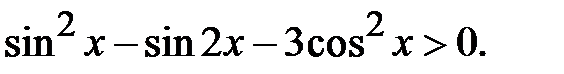
Розв’язання. Запропоновану тригонометричну нерівність перетворимо до алгебраїчної нерівності відносно величини  :
:
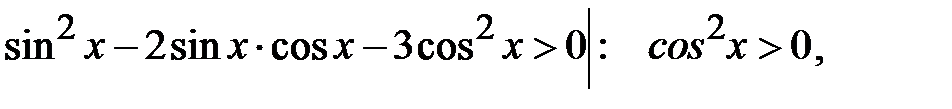

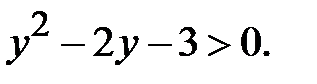
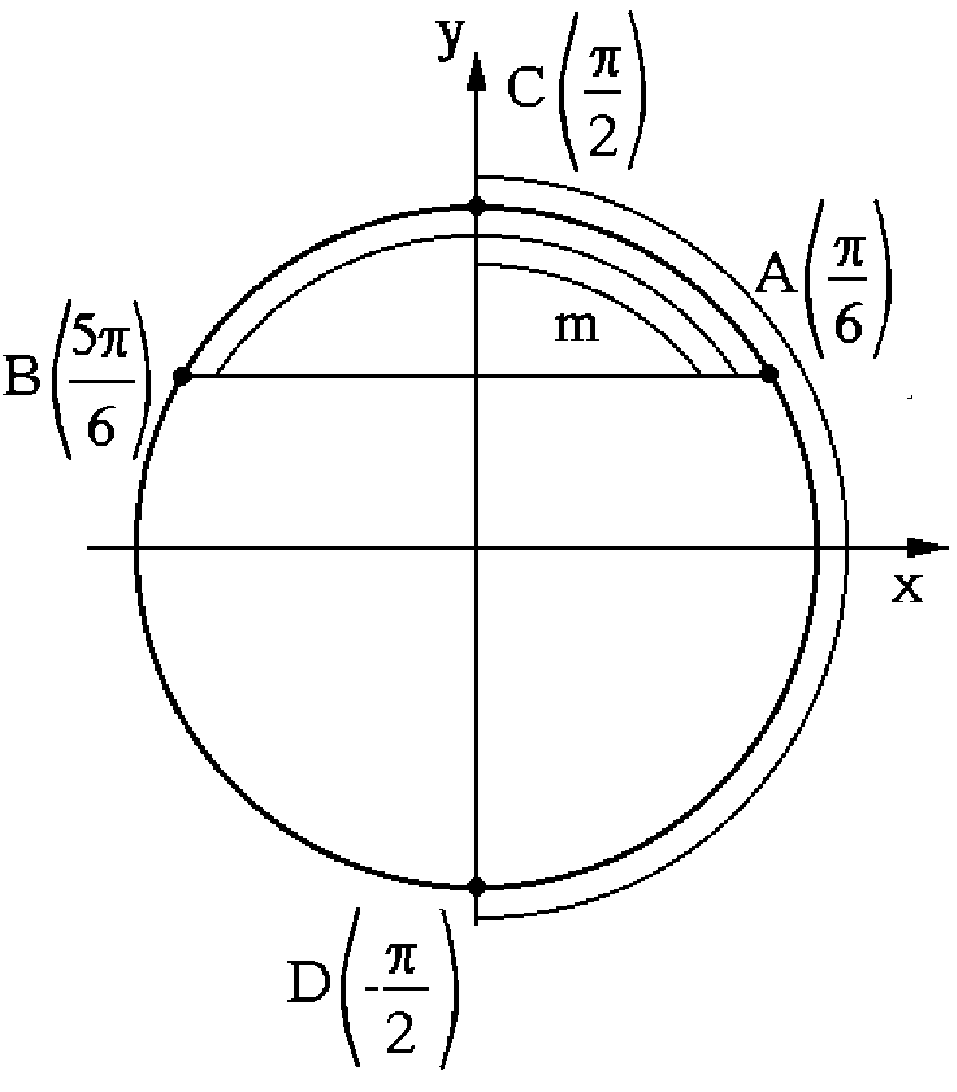 Рис. 5.13
Рис. 5.13
| 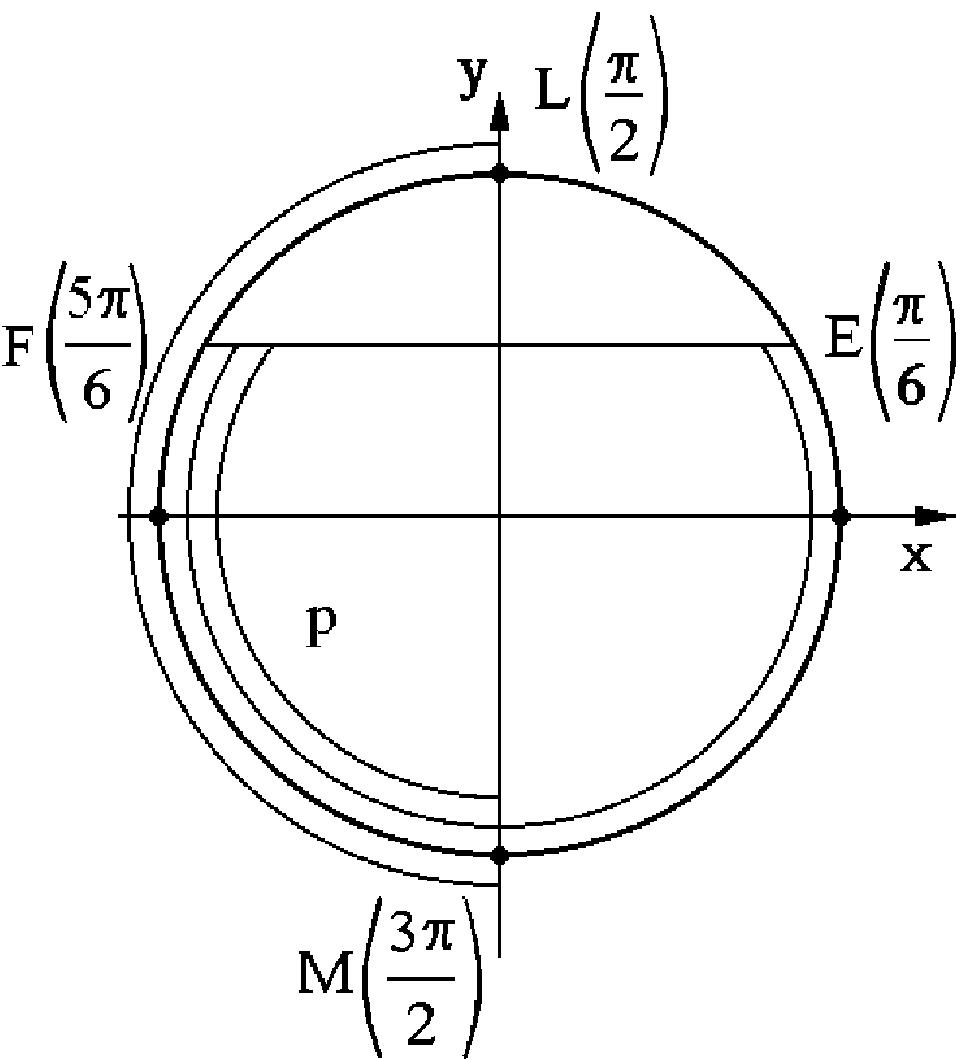 Рис. 5.14
Рис. 5.14
|
Розв’язком останньої нерівності є сукупність множин:
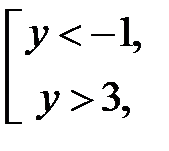 або
або 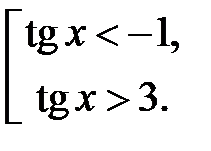
Геометричний розв’язок тригонометричних нерівностей зображено на рис. 5.15 і 5.16. Це дуги DmC, EpF, SpR і PmQ.
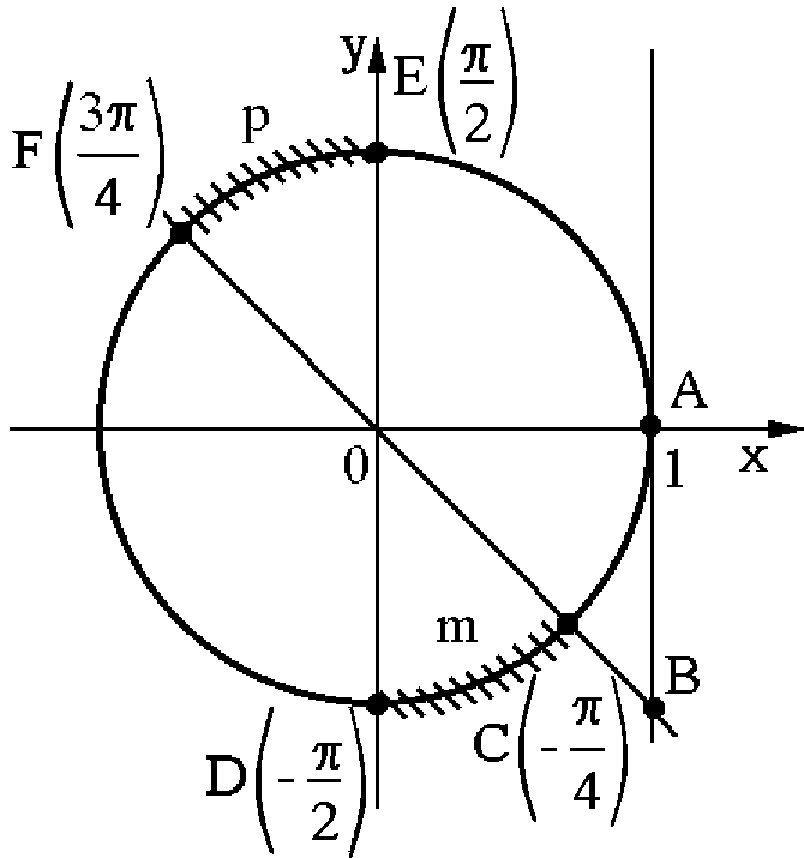 Рис. 5.15
Рис. 5.15
| 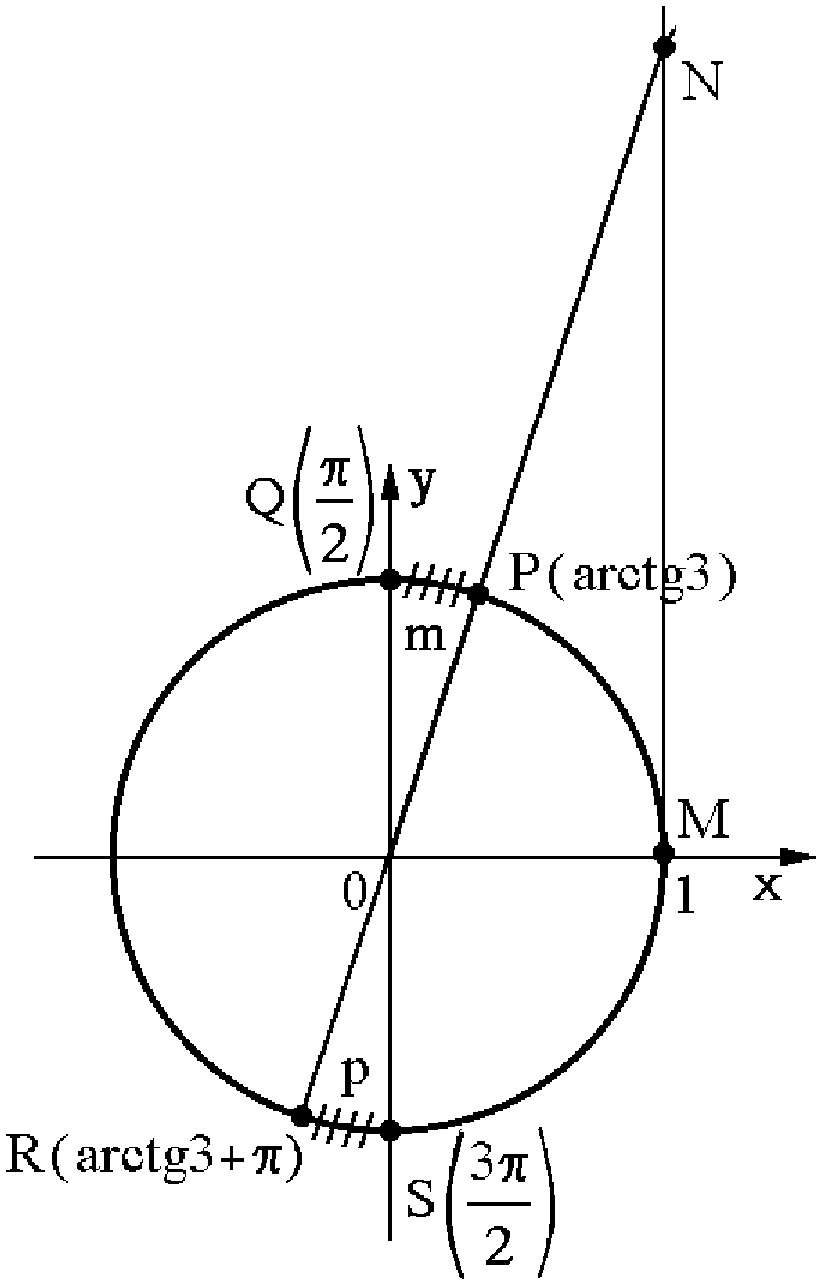 Рис. 5.16
Рис. 5.16
|
Аналітичним розв’язком наведеної нерівності буде множина
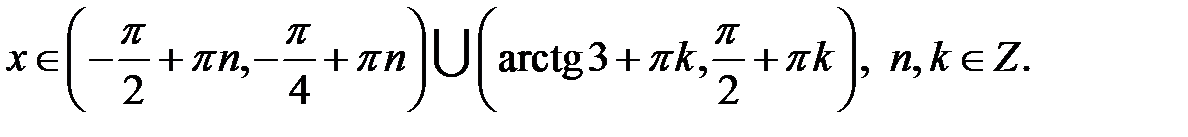
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 730; Нарушение авторских прав?; Мы поможем в написании вашей работы!