
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Биномиальное распределение вероятностей
|
|
|
|
Повторные независимые испытания
Важные закономерности теории вероятностей, имеющие применение в статистике, связываются с рассмотрением независимых повторных испытаний.
Ряд испытаний мы будем называть независимым по отношению к событию А, если вероятность появления А в каждом испытании не зависит от результатов прочих испытаний.
Примерами повторных испытаний такого вида могут служить:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается);
3) лотерейное определение номера облигации выигрышного займа, на которую падает выигрыш, по каждой из серий, дающих выигрыш для одной облигации (здесь выпадение определенного номера облигации имеет одну и ту же вероятность для любой серии).
Пусть при выполнении п повторных независимых испытаний требуется найти вероятность появления события А точно т раз, если появление события А в каждом отдельном испытании имеет вероятность, равную р (появление противоположного события А имеет вероятность  ).
).
Обращаясь сначала к частному случаю, например при п= 3, т =2, мы можем установить, что двукратное появление события А связано с однократным появлением события А (противоположного) и что такой исход испытания может иметь место в одном из следующих расположений:
или  или
или 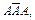 или
или 
Вероятности каждого из этих сложных событий равны между собой и определяются по теореме умножения вероятностей:
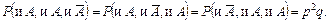
Ответ на вопрос о вероятности появления события А два раза (и события  один раз) при трех повторных испытаниях требует применения теоремы сложения вероятностей. Это дает1):
один раз) при трех повторных испытаниях требует применения теоремы сложения вероятностей. Это дает1):
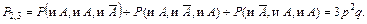
Пример 1. В принятой партии хлопка число длинных волокон составляет  их общего числа. Какова вероятность того, что в пучке хлопка из 3 волокон окажутся 2 длинных волокна?
их общего числа. Какова вероятность того, что в пучке хлопка из 3 волокон окажутся 2 длинных волокна?
Решение. Здесь имеем

а отсюда
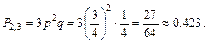
Чтобы обобщить выражение коэффициента 3, найденного при условии п=3 и т=2, рассмотрим случай n =4 и т= 2.
Здесь двукратное появление события A сопровождается двукратным появлением и события  , а это возможно в следующих комбинациях:
, а это возможно в следующих комбинациях:
 , или
, или 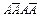 , или
, или 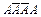 , или
, или  , или
, или  , или
, или 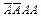 .
.
Число этих комбинаций при одинаковой вероятности появления каждой из них определяет
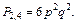
Из теории соединений (комбинаторики) мы знаем, что 3 есть число сочетаний из трех элементов по два и что 6 есть число сочетаний из четырех элементов по два.
Применением метода математической индукции можно установить, что появление события A два раза при n испытаниях имеет 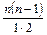 комбинаций (это — число сочетаний из п элементов по два), а появление т раз события А при п испытаниях имеет
комбинаций (это — число сочетаний из п элементов по два), а появление т раз события А при п испытаниях имеет  комбинаций (число сочетаний из п элементов по m).
комбинаций (число сочетаний из п элементов по m).
Заметив далее, что появление каждой отдельной комбинации, в которой событие А участвует два раза, например

имеет вероятность 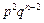 , мы устанавливаем, применяя теорему сложения, что
, мы устанавливаем, применяя теорему сложения, что

Аналогично появление отдельной комбинации, в которой событие А участвует т раз, например
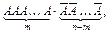
имеет вероятность 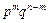 , а поэтому по теореме сложения получаем
, а поэтому по теореме сложения получаем

Применяя для числа 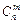 известную формулу
известную формулу
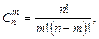
мы получим выражение вероятности появления события А при п независимых испытаниях ровно т раз в виде

Это — формула Бернулли.
Пример 2. Вероятность попадания в цель составляет при отдельном выстреле р = 0,8. Найти вероятность пяти попаданий при 6 выстрелах.
Решение. Здесь п = 6, т = 5, р = 0,8, q = 0,2. Поэтому искомая вероятность

Переходим теперь к дальнейшему обобщению результата, выражающего вероятность появления некоторого события заданное число раз. при выполнении п испытаний, независимых по отношению к этому событию.
Правая часть формулы Бернулли представляет собой общий член разложения бинома Ньютона. Поэтому, если мы будем придавать числу т появлений события А значения  , то получим соответствующие выражения вероятностей:
, то получим соответствующие выражения вероятностей:
 — вероятность появления события А во всех испытаниях;
— вероятность появления события А во всех испытаниях;
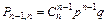 — вероятность появления события А во всех испытаниях, кроме одного;
— вероятность появления события А во всех испытаниях, кроме одного;
 — вероятность появления события А в п - 2 испытаниях;
— вероятность появления события А в п - 2 испытаниях;
…………………………………………………………………………………………………………………………………
 — вероятность появления события А в трех испытаниях;
— вероятность появления события А в трех испытаниях;
 — вероятность появления события А в двух испытаниях;
— вероятность появления события А в двух испытаниях;
 — вероятность появления события А в одном испытании;
— вероятность появления события А в одном испытании;
 — вероятность непоявления события А ни в одном испытании (появления события А во всех п испытаниях).
— вероятность непоявления события А ни в одном испытании (появления события А во всех п испытаниях).
При п независимых испытаниях только и возможно, т. е. достоверно, появление события А либо п, либо п- 1, либо n -2,..., либо 3, либо 2, либо 1 раз, либо ни разу, а это означает, что

и, таким образом, известная формула разложения бинома Ньютона
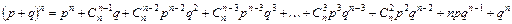
дает распределение вероятностей появления события А между всеми единственно возможными и несовместимыми результатами проведения п независимых испытаний. При этом, заметив, что 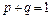 , мы устанавливаем, что и левая часть формулы дает
, мы устанавливаем, что и левая часть формулы дает 
Биномиальное распределение вероятностей позволяет определить не только вероятность появления интересующего нас события заданное число раз при n независимых испытаниях, но и вероятность того, что число т случаев появления этого события заключено в заданных границах между числами 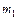 и
и  , либо оказывается больше (меньше) или не меньше (не больше) данного числа
, либо оказывается больше (меньше) или не меньше (не больше) данного числа 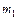 .
.
Покажем это на ряде примеров.
Пример 3. Всхожесть семян данного сорта растений оценивается вероятностью 0,8. Какова вероятность, что из 5 посеянных семян взойдет не меньше 4?
Решение. Имеем п= 5,  и
и 
 , т. е. т принимает значения или 4, или 5. Искомая вероятность
, т. е. т принимает значения или 4, или 5. Искомая вероятность
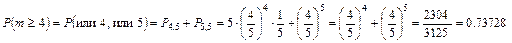 1).
1).
Пример 4. По данным ОТК на сотню металлических брусков, заготовленных для обработки, приходится 30 с зазубринами. Какова вероятность, что из случайно взятых 7 брусков окажется без дефектов не более двух?
Решение. Пусть событием А здесь будет отсутствие на бруске зазубрин. Тогда  и
и  . Число испытаний
. Число испытаний 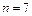 , а
, а  т. е. принимает значение или 2, или 1, или 0.
т. е. принимает значение или 2, или 1, или 0.
Искомая вероятность

Пример 5. При установившемся технологическом режиме зафиксировано 120 обрывов на 1000 веретен в час. Определить вероятность того, что число обрывов в час на 25 веретенах будет больше двух, но меньше восьми.
Решение. Здесь для  получим
получим  и
и  . Принимая
. Принимая 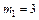 и
и 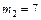 , будем иметь
, будем иметь 
Искомая вероятность запишется в виде 
и определится по теореме сложения:

В связи с последним примером следует заметить, что использование биномиального закона зачастую связано с вычислительными трудностями. Поэтому с возрастанием значений п и т становится целесообразным применение приближенных формул, что будет рассмотрено в последующих параграфах.
Для небольших значений п и т биномиальное распределение дает возможность сравнительно легко установить доли отдельных членов разложения, выявить, какое число появлений события А наиболее вероятно, и определить, как меняются вероятности с изменением числа появлений данного события.
Пример 6. Пусть производится 8 независимых испытаний, причем вероятность появления события А в каждом испытании 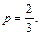 Найти вероятности возможных исходов.
Найти вероятности возможных исходов.
Решение. Для этих условий биномиальное распределение дает:
| m | 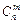
| 
|

| 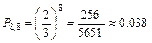
| |
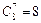
| 
| |
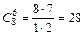
| 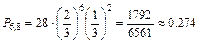
| |

| 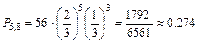
| |
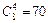
| 
| |
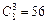
| 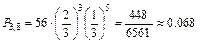
| |
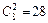
| 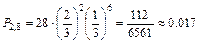
| |

| 
| |
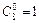
| 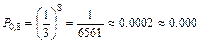
|
Полученные результаты можно наглядно представить графически. В прямоугольной системе координат по горизонтальной оси откладываются числа т (появлений события А), а из этих точек восстанавливаются перпендикулярные отрезки, представляющие значения соответствующих вероятностей  . Концы этих перпендикуляров последовательно соединяются прямыми отрезками, и, таким образом, получается многоугольник распределения вероятностей. Для нашего примера этот многоугольник представлен на рис. 1, причем для большей наглядности выбраны неодинаковые по горизонтальной и вертикальной осям масштабы.
. Концы этих перпендикуляров последовательно соединяются прямыми отрезками, и, таким образом, получается многоугольник распределения вероятностей. Для нашего примера этот многоугольник представлен на рис. 1, причем для большей наглядности выбраны неодинаковые по горизонтальной и вертикальной осям масштабы.

Рис. 1.
Распределение вероятностей в приведенном примере показывает, что наиболее вероятны здесь 5 и 6 появлений события А и что непоявление ни разу события А практически исключается. И цифровые данные, и чертеж показывают, что с ростом числа т соответственные вероятности сначала увеличиваются, а затем, после достижения наибольших значений, уменьшаются.
Пример 7. Длительной проверкой качества стандартных деталей установлено, что из каждой сотни деталей не имеют дефектов 75 штук в среднем. Составить биномиальное распределение вероятностей числа пригодных деталей из взятых наудачу 6 деталей.
| m | 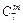
| 
|

| 
| |

| 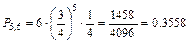
| |

| 
| |
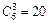
| 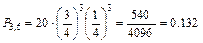
| |

| 
| |
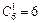
| 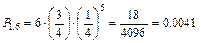
| |

| 
|
Эти результаты показывают, что наиболее вероятным оказывается наличие пяти пригодных деталей из шести и что практически можно рассчитывать на пригодность не менее трех деталей, поскольку
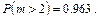
Графическое представление этого распределения дано на рис. 2.

Рис. 2.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 1924; Нарушение авторских прав?; Мы поможем в написании вашей работы!