Наивероятнейшее число появлений события

Биномиальное распределение, как мы видели, позволяет, в частности, установить, какое число появлений события А наиболее вероятно. В примере 6 такое число имело два значения: 5 и 6, а в примере 7 таким числом оказалось 5.

Здесь мы покажем, что отыскание такого числа может быть выполнено непосредственно без составления полного биномиального распределения.

Обозначая искомое число через 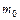, мы должны составить условия, обеспечивающие для него наибольшую вероятность. Это значит, что соответственный член биномиального распределения должен принимать наибольшее значение, т. е. должен удовлетворять неравенствам:

(1)

и

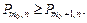(2)

Воспользуемся формулой общего числа члена биномиального разложения. Из неравенства (1)

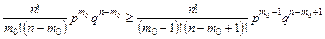
после сокращений получаем

или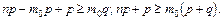

Отсюда (так как р + q = 1)

. (3)

Из неравенства (2)

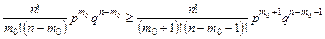
после сокращений получаем

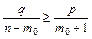
или

Отсюда

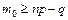. (4)

Объединяя неравенства (3) и (4), мы получаем двойное неравенство

, (5)

устанавливающее границы для числа .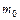

Так как , то эти границы отличаются на 1. Поэтому 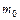, являющееся целым числом, может принимать либо одно значение, когда пр целое число 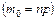и когда 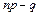(а отсюда и пр+р) нецелое число, либо два значения, когда 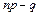целое число.

Пример 8. При автоматической наводке орудия вероятность попадания по быстро движущейся цели равна 0,9. Найти наивероятнейшее число попаданий при 50 выстрелах.

Решение. Здесь 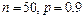и 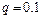. Поэтому имеем неравенства:

Отсюда

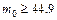и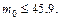

Следовательно,

Пример 9. Данные длительной проверки качества выпускаемых стандартных деталей показали, что в среднем брак составляет 7,5%. Определить наиболее вероятное число вполне исправных деталей в партии из 39 штук.

Решение. Обозначая вероятность выпуска исправной детали через р, будем иметь q = 0,075 и (получение бракованной детали и получение исправной детали — события противоположные). Так как здесь п= 39, то искомое число можно найти из неравенств:

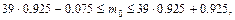или

Отсюда наивероятнейшее число исправных деталей равно 36 или 37.

Выведенные неравенства для 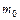позволяют решить и обратную задачу: по данному 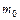и известному значению р определить общее число п всех испытаний.

Пример 10. При каком числе выстрелов наивероятнейшее число попаданий равно 16, если вероятность попадания в отдельном выстреле составляет 0,7?

Решение. Здесь 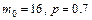и

Составляем неравенства

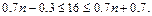
Отсюда

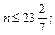
и

и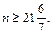

Таким образом, 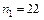и 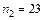, т.е. число всех выстрелов здесь может быть 22 или 23.

Дата добавления: 2014-12-26