Критерий Манна-Уитни

Проверка гипотез в двухвыборочных задачах

Область применения. Рассмотрим часто встречающуюся на практике задачу сравнения двух выборочных совокупностей. В духе основной статистической предпосылки мы будем рассматривать эти совокупности как случайные. Например, нас может интересовать сравнение двух методов обработки, т.е. двух разных действий, направленных к одной цели: двух лекарств, двух рационов питания, двух методик обучения или профессиональной подготовки и т.д.

Данные. Для исследования нужны однородные объекты, разделенные на две группы. Взаимные влияния и взаимодействия объектов должны быть исключены. Для каждого объекта регистрируется некоторая его числовая характеристика. Возникающие при этом две группы чисел можно рассматривать как две независимые выборки.

Постановка задачи. Рассмотрим вопрос о том, какие задачи целесообразно рассматривать при сравнении двух выборок. Вспомним, что обычно две выборки получаются как характеристики двух обработок, то есть как результаты применения различных условий эксперимента к двум группам однородных объектов. Опыт применения статистики показывает, что изменение условий эксперимента обычно сказывается прежде всего на изменении положения распределения измеряемой числовой характеристики на числовой прямой. Масштаб и форма распределения при малых изменениях условий эксперимента обычно остаются практически неизменными. При больших различиях в условиях эксперимента наряду с изменением положения распределения изменяется и его разброс (дисперсия). И совсем редко происходит изменение самой формы распределения. Поэтому при исследовании различий в двух выборках часто предполагают, что законы распределения двух анализируемых выборок отличаются только сдвигом, т.е. принадлежат сдвиговому семейству распределений.

Определение. Распределение G (x) принадлежит сдвиговому семейству распределений F, задаваемому распределением F (x), если существует такая q, что для любого .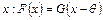

Другими словами, если случайная величина x имеет распределение F (x), то распределение G (x) случайной величины h принадлежит сдвиговому семейству F тогда и только тогда, когда для некоторого неслучайного числа q распределения случайных величин h и совпадают.

Для некоторых сдвиговых семейств (например, для семейства, порожденного нормальным распределением) построены весьма эффективные критерии для проверки гипотезы Н против альтернатив сдвига 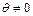. Однако эти критерии предполагают, что F и G принадлежат определенному семейству, а поэтому могут давать неправильные результаты при невыполнении этого условия. Другой класс критериев — непараметрические критерии, — не требует этого предположения. Такие критерии не зависят от распределений F и G (если эти распределения непрерывны), и эффективно работают при более широком классе альтернатив. В частности, с их помощью можно найти различия в случайных величинах при альтернативах 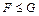и . Дадим определения этих понятий.

Определение. Мы говорим, что , где F и G — функции распределения, если для любого числа х выполняется 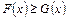. Мы говорим, что 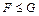, если для любого числа х выполняется .

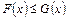Смысл этого определения состоит в том, что при случайная величина X, имеющая закон распределения F, имеет тенденцию принимать меньшие значения, чем случайная величина Y с законом распределения G, т.е. для любого х выполняется .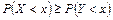

Методы. Ниже мы расскажем, как проверить однородность двух выборок с помощью критерия Манна-Уитни или критерия Уилкоксона.

Область применения критерия Манна-Уитни — анализ двух независимых выборок. Размеры этих выборок могут различаться.

Назначение критерия — проверка гипотезы о статистической однородности двух выборок. Иногда эту гипотезу называют гипотезой об отсутствии эффекта обработки (имея в виду, что одна из выборок содержит характеристики объектов, подвергшихся некоему воздействию, а другая — характеристики контрольных объектов).

Данные. Рассматриваются две выборки 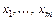(выборка х) и 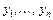(выборка у) объемов m и п. Обозначим закон распределения первой выборки через F, а второй — через G.

Допущения. 1. Выборк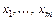и и 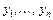должны быть независимы.

2. Законы распределений F и G непрерывны. Отсюда следует, что с вероятностью 1 среди чисел 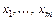и 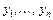нет совпадающих.

Гипотеза. Утверждение об однородности выборок 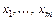и 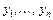в введенных выше обозначениях можно записать в виде H: F = G.

Альтернативы. В качестве альтернатив к H могут выступать все возможности F ¹ G. Однако критерий Манна-Уитни способен обнаруживать отнюдь не все возможные отступления от Н: F = G. Этот критерий предназначен, в первую очередь, для проверки Н против альтернативы (правосторонняя альтернатива, "перетекание" вероятностей вправо) или альтернативы 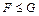(левосторонняя альтернатива, т.е. уход вероятностей влево). Можно рассматривать и объединение обеих возможностей (двусторонняя альтернатива).

Метод. Критерий Манна-Уитни повторяет основные идеи критерия знаков и в определенном смысле является его продолжением. Он основан на попарном сравнении результатов из первой и второй выборок.

Условимся, что всякое событие обозначает «успех», а всякое событие 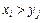— «неудачу». Смысл такой терминологии может быть связан с тем, что мы предполагаем, что вторая группа лучше первой, и рады подтверждению наших представлений. Изменяя i от 1 до m и j от 1 до п, получаем тп парных сравнений элементов выборок х и у. Обозначим число успехов в этих парных сравнениях через U. Ясно, что U может принимать любое целое значение от 0 до тп.

Дата добавления: 2014-12-26