Критерий знаков для анализа парных повторных наблюдений

Парные наблюдения

Рассмотренное в предыдущем параграфе сравнение двух совокупностей наблюдений (двух выборок) часто проводится для обнаружения результата какого-либо воздействия (выявления эффекта обработки), либо, напротив, для подтверждения его отсутствия. Чем более однородными окажутся выбранные для эксперимента объекты (для контроля и воздействия), чем меньше их случайные различия, тем точнее (и по меньшему числу наблюдений) можно будет дать ответ на вопрос. Кстати, формирование однородной группы экспериментальных объектов составляет важную и не всегда простую задачу.

Ясно, что различие между объектами, выбранными для воздействия и для контроля (или для двух разных воздействий, если интерес представляет их сопоставление) будет наименьшим, если в обоих качествах выступает один и тот же объект. Если это возможно, то далее обычным порядком мы составляем группу экспериментальных объектов (по-прежнему стремясь к тому, чтобы они были однородны — значение этого выяснится в п. 6.2). Далее для каждого объекта мы измеряем два значения интересующей нас характеристики (например, до воздействия и после или при двух разных воздействиях). Так возникают пары наблюдений и парные данные. Но, конечно, парные данные могут возникать и иначе (скажем, при наблюдениях над близнецами, которые во многих отношениях считаются идентичными).

Назначение. Критерий знаков используется для проверки гипотезы об однородности наблюдений внутри каждой пары (иногда говорят — для проверки гипотезы об отсутствии эффекта обработки).

Данные. Рассмотрим совокупность случайных пар объема п. Введем величины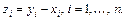

Допущения. 1. Все 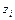предполагаются взаимно независимыми. Заметим, что мы не требуем независимости между элементам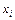и и 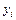с одинаковым номером i. Это весьма важно на практике, когда наблюдения делаются для одного объекта и тем самым могут быть зависимы.

2. Все z_i имеют равные нулю медианы, т.е. . Подчеркнем, что законы распределения разных z_i могут не совпадать.

Гипотеза. Утверждение об отсутствии эффекта обработки для повторных парных наблюдений можно записать в виде для всех i= 1,..., n.

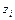Метод. 1. Перейдем от повторных парных наблюдений к величинам , i= 1,..., n, введенным выше.

2. К совокупности 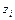, i= 1,..., n применим критерий знаков для проверки гипотезы о равенстве нулю медиан распределений величин 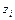, i= 1,..., n (см. п. 4.2).

Приближение для больших совокупностей. Следует воспользоваться нормальной аппроксимацией биномиального распределения.

Связанные данные. Если среди значений 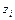есть нулевые, то их следует отбросить и соответственно уменьшить n до числа ненулевых значений .

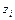Оценка эффекта обработки. Нередко для 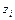рассматривают модель , , 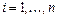где — ненаблюдаемые случайные величины, q — некоторая константа, характеризующая положение одного распределения относительно другого (скажем, до воздействия и после). Эту константу часто именуют эффектом обработки. Принятые выше допущения 1 и 2 переносятся на величины 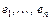. Гипотеза однородности формулируется в виде гипотезы о нулевом эффекте обработки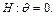

Введенные величины q и представления оказываются полезными, если в ходе проверки гипотезы выясняется, что 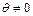и что поэтому надо оценить количественно то различие, которое привносит обработка (воздействие).

Пример. Покажем как использовать критерий знаков для анализа данных о времени реакции на звук и на свет. В этом примере рассматривается группа испытуемых, а целью исследования служит проверка гипотезы о равенстве времени реакций на звук и на свет. Порядок организации эксперимента позволяет предположить, что полученные данные на одном испытуемом независимы от аналогичных данных для остальных.

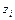Осуществим переход от пар к величинам , i= 1,..., n и запишем последние в виде: , .

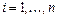Выполняются ли для сформулированной задачи допущения, используемые в критерии знаков? Независимость обеспечивается условиями организации эксперимента. Априорно предполагаемая непрерывность распределений рассматриваемых выборок обеспечивает непрерывность распределения . В случае совпадения распределений времени реакции на звук и на свет справедливо следующее соотношение . Следовательно, , то есть медиана распределения 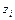равна нулю. Таким образом, предположение 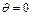обеспечивает выполнение допущения 2.

Одной из разумных альтернатив нулевой гипотезе в данном случае является предположение о том, что 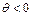. Далее мы будем использовать критерий знаков против этой односторонней альтернативы.

В табл. 5 приведены соответствующие расчеты для данного примера.

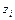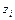Обозначим число положительных значений через . Из таблицы 5 видно, что равно трем, а среди есть одно значение, равное 0. В таких случаях необходимо уменьшить число наблюдений 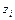на число значений 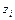, равных 0, т.е. перейти от п = 17 к п = 16.

Вычислим вероятность . Для этого воспользуемся таблицами биномиального распределения при , п = 16. Учитывая, что в силу симметрии при 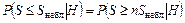,получаем:

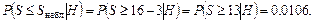
То есть минимальный уровень значимости, на котором можно отвергнуть гипотезу о том, что 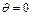против односторонних альтернатив, равен 0.0106. Учитывая малость этого числа, заключаем, что гипотезу следует отвергнуть в пользу альтернативы .

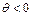Таблица 5

i	xi	yi	zi	S (xi)
			-42	-
				+
			-36	-
			-30	-
			-12	-
				+
			-52	-
			-20	-
			-45	-
			-35	-
			-19	-
			-23	-
			-10	-
			-7	-
			+7	+
			-19	-

Обсуждение. Одно из главных достоинств критерия знаков — его простота. Другой важной особенностью этого критерия являются скромные требования к первоначальному статистическому материалу. Эти требования описываются с помощью модели парных наблюдений.

6.2. Анализ повторных парных наблюдений с помощью знаковых рангов (критерий знаковых ранговых сумм Уилкоксона)

Если можно дополнительно предположить, что случайные величины из предыдущего пункта непрерывны и одинаково распределены, то для проверки гипотезы однородности можно применить более мощный критерий, основанный на статистике Т знаковых ранговых сумм Уилкоксона.

Метод. 1. Вычислим абсолютные разности 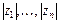. Пусть R_i обозначает ранг 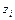в совместном упорядочении 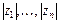от меньшего к большему.

2. Определим переменные , где

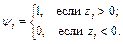
3. Вычислим наблюденное значение 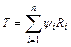, далее мы будем называть его .

4. Для одностороннего критерия для проверки против правосторонней альтернативы 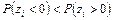на уровне значимости a:

• отклонить Н, если

• принять Н, если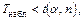

где критическое значение удовлетворяет уравнению и может быть найдено по соответствующей таблице.

Для одностороннего критерия для проверки той же гипотезы против левосторонней альтернативы 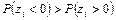на уровне значимости a:

• отклонить Н, если

• принять Н, если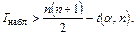

Для двустороннего критерия для проверки той же гипотезы Н против двусторонних альтернатив 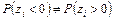на уровне значимости 2 a:

• отклонить Н, если или

• принять Н, если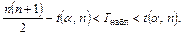

Замечание. Поскольку распределение статистики Т дискретно, уравнение, определяющее 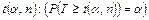имеет точное решение не для всех значений a (при фиксированном п). Поэтому либо в качестве придется взять приближенное решение, либо изменить a так, чтобы уравнение можно было решить точно.

Приближение для большой выборки. При выполнении гипотезы Н статистика

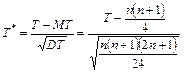
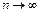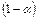имеет асимптотическое (при ) распределение N (0, 1). Приведем приближение нормальной теории для проверки Н, для определенности, против правосторонней альтернативы: Н отклоняется, если ,в противном случае Н принимается. Здесь — квантиль уровня стандартного нормального распределения N (0, 1). Остальные правила трансформируются аналогично.

Совпадения. Если среди значений 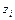есть нулевые, то их следует отбросить, соответственно уменьшив п до количества ненулевых значений z_i. Если среди ненулевых значений есть равные, то для вычисления Т надо использовать средние ранги для величин 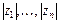и далее использовать те же методы, что и без совпадений. Для приближения для больших выборок рекомендуется в формуле для вычисления T ^* значение DT заменить на

где g — число связок, 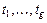— их размеры. Определение связок смотри в разделе 5.2 при обсуждении статистики W ^*.

Список использованной литературы

1. Курс высшей математики с элементами теории вероятностей и математической статистике. Маркович Э. С. – М., «Высш. школа», 1972.

2. Статистический анализ данных на компьютере. Тюрин Ю. Н. и Макаров А. А. – М., «ИНФРА-М», 1998.

Список рекомендуемой литературы

1. Что могут дать обществоведам современная статистика и статистическая логика? Григорьян Э. Р. – М., // Статистические методы в общественных науках. С. 5 – 29., 1982.

2. Математические методы в социальных науках: Сб. статей / Под ред. П. Лазарсфельд и Н. Генри. - М.: Прогресс, 352 с., 1973.

3. Логика прикладного статистического анализа. Елисеева И. И., Руковишников В. О. – М.: Статистика, 192 с., 1982.

4. Как правильно пользоваться статистикой. Г. Кимбл. – М.: Финансы и статистика., 295 с., 1982.

5. Математические методы в социологическом исследовании. М.: Наука., 335 с., 1981.

6. Проверка статистических гипотез. Э. Леман. – М.: Наука., 408 с., 1979.

7. Достоверность статистических показателей. Эдельгауз Г. Е. – М.: Статистика, 278 с., 1977.

8. Математические методы обработки обработки статистической информации с помощью ЭВМ. Репин С. В., Шеин С. А.: Пособие для исследователей гуманит. спец. – Мн.: Университетское, 128 с., 1990.

1) Игральной костью называется кубик с круглоотточенными вершинами, на каждой грани которого помещены кружочки. На одной грани этого кубика находится один кружок, на другой — 2, на третьей — 3, на четвертой — 4, на пятой — 5 и на шестой — 6.

1) Имеется в виду, что эта система удовлетворяет условиям, установленным в предыдущем параграфе.

1) По смыслу вероятности совместного наступления двух событий ясно, что она должна быть симметрична относительно А и В. Поэтому, или

Это свойство легко проверить на примере 8, если искать вероятность появления белого и небелого шаров. В самом деле, обозначая через А появление белого шара и через В — небелого, имеем;

а) при появлении сначала белого шара

б) при появлении сначала небелого шара

1) Здесь Р _2,3 обозначает вероятность появления события А два раза при трех повторных испытаниях. Соответственно Р_m,n будет обозначать вероятность появления т раз события А при п повторных испытаниях.

1) Если при таком же значении п=5 требуется найти вероятность того, что число взошедших семян меньше 4, т. е. вычислить Р (m < 4), то непосредственное суммирование связано с отысканием по формуле Бернулли четырех слагаемых, что является слишком громоздкой операцией. Использование того, что Р (т < 4)+ Р (m ³ 4) = 1, позволяет проще найти искомую вероятность с помощью вычитания: Р (т < 4) = 1 - Р (m ³ 4). Такой прием вычисления выгоден в ряде примеров.

1) Эта формула называется асимптотической, так как она тем точней, чем больше.

2) Впервые формула такого вида была получена для случая в 1730 г. Муавром, а обобщение ее для любого было проведено Лапласом. Поэтому правильней было бы называть эту формулу локальной теоремой Муавра — Лапласа.

3) При наличии специальных таблиц с логарифмами факториалов отпадает необходимость преобразования выражения.

1) Здесь для большей наглядности приняты различные масштабы по осям.

1) Практически вместо непосредственного вычисления по этой формуле следует пользоваться таблицей значений функции Пуассона.

1) Эти соотношения между a и b и соответствующими им числами a и b будут применяться ниже при решении задач с помощью этой теоремы.

1) Иногда говорят также «интегральный закон распределения»

1) Действительно

1) Нумерация значений случайной величины обычно дается в порядке их возрастания.

1) Случайные величины называются попарно независимыми, если для любых i и j (от 1 до п) случайные величины и независимы.

1) Рамки настоящего курса не позволяют дать полное содержание этого закона, но и изложенные предложения могут быть использованы для их практического приложения.

1) Вместо e здесь использован символ D, принятый для обозначения ошибки репрезентивности как предела отклонения.

2) Здесь m — средняя ошибка репрезентативности при определении средней признака в случае повторной выборки.

1) Полученное из наблюдения распределение случайной величины Х позволяет определить для каждого значения х частость всех значений Х < х. Обозначая эту частость в виде [здесь т (х) — число наблюдений, в которых Х < х, а п — число всех наблюдений], можно выразить эмпирическую функцию распределения в виде.

1) При вычислении значений для точности и удобства подсчетов исходим из того, что.

1) При вычислении значений для большей точности и удобства подсчетов исходим из того, что

.

1) К слову сказать, теория движения Луны должна быть очень точной, ибо у нас (у человечества) есть очень мощные возможности ее проверки — Лунные и Солнечные затмения, сведения о которых сохранились в истории за многие тысячелетия. Теория должна не только достаточно точно предсказывать даты близящихся затмений (что относительно нетрудно), но и рассчитывать эти даты на много веков назад и получать при этом верные результаты. Такой точности добиться нелегко.

Дата добавления: 2014-12-26