Понятие о множественной корреляции

Этот вид корреляционной зависимости возникает в тех случаях, когда рассматривается связь между тремя или большим числом признаков, характеризующих изучаемое явление.

Ограничиваясь линейной корреляционной связью между величиной z и аргументами х и у, общий вид которой

,

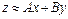заметим, что эту связь выгодней рассматривать в форме зависимости между отклонениями величин х, у и z от их средних х, у и z. Этим требуемая корреляционная зависимость приводится к виду

.

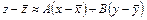Коэффициенты этого уравнения А и В выражают коэффициенты регрессии, которые определяются по формулам:

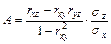и .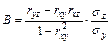

Компонентами этих коэффициентов служат коэффициенты корреляции между х и у 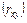, х и z 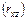и y и z 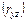, а также соответственные соотношения между средними квадратическими отклонениями величины z и каждого аргумента (х и у).

Такая структура коэффициентов регрессии А и В показывает, что для составления линейного корреляционного уравнения между тремя величинами требуется предварительное вычисление трех коэффициентов корреляции — между аргументами х и у, а также между каждым аргументом и величиной z. Эти же коэффициенты корреляции используются в выражении сводного коэффициента корреляции, определяющего тесноту корреляционной связи между тремя величинами х, у и z: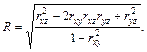

Этот коэффициент принимает значения . При R =0линейная связь между х, у,и z отсутствует, а при R= 1 между ними имеется точная линейная связь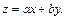

Упражнения

1. Результаты медицинского обследования 100 мужчин по объему грудной клетки в см (х)и общему росту (у) дали следующую таблицу:

y x							Итого
			13 11
Итого

По данным этой таблицы составить уравнения прямых регрессии и вычислить коэффициент корреляции.

Отв. r= 0,79.

2. При обследовании 50 учеников 4-го класса получены следующие данные о росте и весе учащихся:

Вес(кг) Рост (см)
	1

По данным обследования определить коэффициент корреляции и составить уравнение регрессии, связывающие рост ученика и его вес.

Отв. r =0.87.

Раздел 2. Основы проверки статистических гипотез

Во многих случаях нам требуется на основе тех или иных данных решить, справедливо ли некоторое суждение. Например, верно ли, что два набора данных исходят из одного и того же источника? Что A - лучший стрелок, чем В? Что от дома до работы быстрее доехать на метро, а не на автобусе, и т.д. Если мы считаем, что исходные данные для таких суждений в той или иной мере носят случайный характер, то и ответы можно дать лишь с определенной степенью уверенности, и имеется некоторая вероятность ошибиться. Например, предложив двум персонам А и В выстрелить по три раза в мишень и осмотрев результаты стрельбы, мы лишь предположительно можем сказать, кто из них лучший стрелок: ведь возможно, что победителю просто повело и он по чистой случайности стрелял намного точнее, чем обычно, либо наоборот, проигравшему не повезло, так как он стрелял намного хуже чем обычно. Поэтому при ответе на подобные вопросы хотелось бы не только уметь принимать наиболее обоснованные решения, но оценивать вероятность ошибочности принятого решения.

Рассмотрение таких задач в строгой математической постановке приводит к понятию статистической гипотезы. В этом разделе мы обсуждаем, что такое статистические гипотезы, какие существуют способы их проверки, каковы наилучшие методы действий и с какими понятиями они связаны. Мы проиллюстрируем эти понятия на примере нескольких важных и часто встречающихся ситуаций, и на этих же примерах покажем, как естественные проблемы надо переводить на математикостатистический язык, чтобы они могли стать предметом статистического исследования. Среди задач, рассматриваемых в этом разделе — проверка гипотез в схеме испытаний Бернулли, гипотез о положении одной выборки и о взаимном смещении двух выборок.

Дата добавления: 2014-12-26