
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейная корреляция
|
|
|
|
Этот вид корреляционной зависимости весьма важен, так как очень многие корреляционные связи, характерные для количественных признаков наблюдаемых однородных фактов, близки к линейным. Данные наблюдения, представленные в виде корреляционной таблицы, и найденные из этой таблицы пары соответственных значений х и 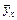 или у и
или у и  , используются для отыскания параметров уравнений прямых регрессии
, используются для отыскания параметров уравнений прямых регрессии
 и
и  .
.
Эта операция, называемая выравниванием, обычно выполняется по способу наименьших квадратов, сущность которого состоит в таком подборе параметров линии регресси, при котором достигается минимум  .
.
Разберем применение данного способа в общем виде для каждого из записанных уравнений регрессии. При этом для иллюстрации используем данные корреляционной таблицы 1 распределения растений житняка по общему весу и по весу семян.
1. Уравнение прямой регрессии у по х. При отыскании по способу наименьших квадратов параметров линейной функции у=ах+b на основании данных наблюдения о парах значений х и у, связанных однозначным соответствием, используется система нормальных уравнений

Здесь коэффициенты определяются простым суммированием слагаемых в соответствии с количеством пар значений х и у.
Если же требуется с помощью способа наименьших квадратов определить параметры уравнения, связывающего значения х с соответственными частными средними 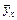 , по данным не простой, а корреляционной таблицы, то структура коэффициентов и свободных членов нормальных уравнений должна отразить все данные корреляционной таблицы.
, по данным не простой, а корреляционной таблицы, то структура коэффициентов и свободных членов нормальных уравнений должна отразить все данные корреляционной таблицы.
а) Коэффициенты, соответствующие суммам  и
и  , должны включать в операцию суммирования все значения х как повторяющиеся, так и неповторяющиеся. Количество значений
, должны включать в операцию суммирования все значения х как повторяющиеся, так и неповторяющиеся. Количество значений  определяется числом
определяется числом  , поэтому сумма этих значений х равна
, поэтому сумма этих значений х равна 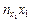 . Аналогично сумма значений
. Аналогично сумма значений  равна
равна  и т. д. Отсюда сумма всех значений х выразится в виде
и т. д. Отсюда сумма всех значений х выразится в виде
|
|
|

Суммирование квадратов переменной х строится также и дает
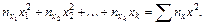
б) Свободный член, соответствующий сумме 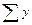 , должен представить сумму всех частных средних
, должен представить сумму всех частных средних 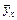 . При этом для каждого значения х количество соответственных частных средних
. При этом для каждого значения х количество соответственных частных средних 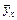 определяется количеством таких значений самого х. Поэтому значению
определяется количеством таких значений самого х. Поэтому значению  соответствует
соответствует  , частных средних
, частных средних 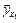 , значению
, значению  соответствует
соответствует  частных средних
частных средних  и т.д. Сумма всех частных средних
и т.д. Сумма всех частных средних 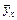 имеет вид
имеет вид
 .
.
в) Свободный член, соответствующий сумме  , должен представить сумму всех возможных произведений значений х на соответствующие частные средние
, должен представить сумму всех возможных произведений значений х на соответствующие частные средние 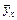 . Количество разных произведений здесь определяется количеством соответственных значений х. Поэтому сумма всех произведений вида
. Количество разных произведений здесь определяется количеством соответственных значений х. Поэтому сумма всех произведений вида  имеет вид
имеет вид
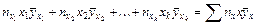 .
.
Удовлетворяющая указанным требованиям система нормальных уравнений для отыскания значений параметров уравнения прямой регрессии  имеет следующий вид:
имеет следующий вид:

Определение корней этой системы предварительно требует некоторого преобразования коэффициентов и свободных членов.
Коэффициенты системы преобразуются так:

Развернутая запись свободного члена  позволяет для каждого слагаемого воспользоваться переходом от частных средних
позволяет для каждого слагаемого воспользоваться переходом от частных средних 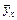 к соответственным частным значениям у.
к соответственным частным значениям у.
В самом деле, если  , то
, то
 .
.
Поэтому
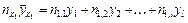
и аналогично
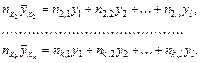
Почленное сложение всех равенств дает в соответствии с принятой структурой корреляционной таблицы 2

После приведения этого результата к выражению, содержащему среднее значение у, получится
 .
.
Преобразование свободного члена  выполняется аналогично. Здесь при
выполняется аналогично. Здесь при  слагаемое
слагаемое 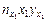 приводится к виду
приводится к виду 
Последующая запись всех остальных слагаемых такого же вида при  ,
,  и суммирование соответствующих выражений дает результат
и суммирование соответствующих выражений дает результат 
|
|
|
Сохраняя эту запись для выполнения подсчетов, можно привести полученный результат к выражению со средним значением ху.
Двойной знак суммирования позволяет выполнять суммирование в любом порядке: сначала по горизонтали (меняя нумерацию частных значений у), а затем по вертикали (меняя нумерацию частных значений х), или, наоборот, сначала по вертикали, а затем по горизонтали.
По структуре корреляционной таблицы: 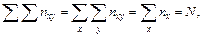
или 
Отсюда 
так как 
В преобразованном виде система такова: 
или 
Для определения параметра a достаточно после умножения членов второго уравнения на 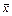 почленно вычесть это уравнение из первого:
почленно вычесть это уравнение из первого: 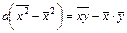 , или
, или 
Параметр b определяется непосредственно из второго уравнения:
 .
.
Подставляя полученное выражение в уравнение прямой регрессии y по х, т. е.  , получим
, получим
 ,
,
или  .
.
Коэффициент а в уравнении прямой регрессии называется коэффициентом прямой регрессии у по х и обозначается символом  .
.
Таким образом, 
и окончательная запись уравнения прямой регрессии y по x таково:
 .
.
Составим такое уравнение с числовыми параметрами для распределения растений житняка по данным корреляционной таблицы 1 об общем весе (x) и весе семян (y) растений. Вычисление необходимых параметров можно проводить по нижеследующей системе подсчетов, соответствующей выполненному общему решению.
1) Составляем вспомогательную таблицу.
2) По данным табл. 4 
Таблица 4
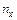
| 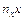
| 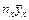 1) 1)
| 
| 
|
| 5×25 | 5×625 | |||
| 10×35 | 10×1225 | |||
| 19×45 | 19×2025 | |||
| 16×55 | 16×3025 | |||
| 11×65 | 11×4225 | |||
| 16×75 | 16×5625 | |||
| 6×85 | 6×7225 | |||
| 6×95 | 6×9025 | |||
| 8×105 | 8×11025 | |||
| 2×115 | 2×13225 | |||
| 1×125 | 1×15625 | |||
| N= 100 |
3) Определяем коэффициент регрессии у по х:

4) Записываем уравнение прямой регрессии у по x:
 ,
,
или окончательно 
2. Уравнение прямой регрессии х по у. Система нормальных уравнений для отыскания параметров с и d уравнения прямой регрессии х по у, получаемая в результате применения способа наименьших квадратов, имеет вид

По аналогии с преобразованиями, проведенными для случая регрессии у по х, можно записать, что
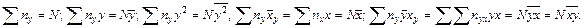
Нормальные уравнения можно переписать в упрощенном виде:
|
|
|

или 
Для определения параметра с из членов первого уравнения вычитаются члены второго уравнения, умноженные на 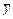 :
:
 ,
,
или 
Параметр d определяется непосредственно из второго уравнения:
 .
.
Замена d этим выражением в уравнении прямой регрессии  дает
дает

или  .
.
Коэффициент с в этом уравнении называют коэффициентом прямой регрессии х по у и обозначают символом 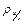 .
.
Таким образом, 
и окончательная запись уравнения прямой регрессии х по у такова:
 .
.
Заметим, что обе прямые регрессии, как видно из их уравнений, проходят через точку 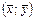 .
.
На примере распределения растений житняка по данным корреляционной таблицы о весе семян (у) и общем весе (х) растений составим уравнение прямой регрессии х по у с числовыми параметрами. Все необходимые вычисления для подсчета параметров проводятся в таком же порядке, как это выполнено для уравнения прямой регрессии у по х.
1) Составляем вспомогательную таблицу.
2) По данным табл. 5

3) Определяем коэффициент регрессии х по у:

Таблица 5
| 
|  1) 1)
| 
| 
|
| 3×13 | 3×169 | |||
| 10×18 | 10×324 | |||
| 20×23 | 20×529 | |||
| 9×28 | 9×784 | |||
| 14×33 | 14×1089 | |||
| 11×38 | 11×1444 | |||
| 9×43 | 9×1849 | |||
| 8×48 | 8×2304 | |||
| 6×53 | 6×2809 | |||
| 6×58 | 6×3364 | |||
| 1×63 | 1×3969 | |||
| 3×68 | 3×4624 | |||
| N= 100 |
4) Записываем уравнение прямой регрессии х по y:
 ,
,
или окончательно 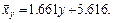
Ниже будет показано, что оба уравнения прямых регрессии могут быть получены одним расчетом с помощью коэффициента корреляции.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!