
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры математической обработки данных выборочного наблюдения
|
|
|
|
Приведенные в предыдущих параграфах сведения позволяют решить ряд примеров, связанных с результатами выборочного наблю дения.
Пример 2. Для определения средней урожайности пшеницы на площади 10000 га определена урожайность на 1000 га. Результаты выборочного обследования представлены в виде следующего распределения:
| Урожайность в ц с га | Количество га |
| 11 – 13 13 – 15 15 – 17 17 – 19 | |
| Итого |
Найти вероятность того, что средняя урожайность пшеницы на всем массиве отличается от средней выборочной не более чем на 0,1 ц, если выборка: а) повторная, б) бесповторная.
Решение. Вычислим среднюю арифметическую и дисперсии данного в условии распределения (это будут выборочная средняя и выборочная дисперсия).
За значение признака нужно принять середины интервалов В результате получим

 .
.
Для нахождения вероятности искомого события применяем формулу
 ,
,
в которой 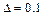 . Найдем среднюю квадратическую ошибку m.
. Найдем среднюю квадратическую ошибку m.
Для повторной выборки по формуле (1), в которой 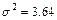 , а п= 1000, получим
, а п= 1000, получим
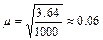 ,
,
а в случае бесповторной выборки имеем по формуле (3)
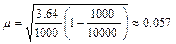 .
.
Если выборка повторная, то вычисление искомой вероятности дает
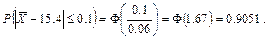
Если же выборка бесповторная, то искомая вероятность

Пример 3. Нз партии, содержащей 8000 деталей, было проверено 1000 деталей. Среди них оказалось 4% нестандартных. Определить вероятность того, что доля нестандартных деталей во всей партии отличается от их доли в выборке (w =0,04) не более чем на 0,015, если выборка: а) повторная, б) бесповторная.
Решение. В соответствии с формулой (2) при w =0,04, п = 1000 средняя квадратическая ошибка повторной выборки
 .
.
Если выборка бесповторная, то в соответствии с формулой (4)при значениях w =0,04, п = 1000 и N= 8000, средняя квадратическая ошибка 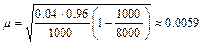 .
.
Отсюда искомая вероятность определяется так:
а) при повторной выборке 
б) при бесповторной выборке 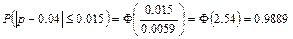 .
.
Пример 4. При условиях приведенного выше примера 2 найти границы, в которых с вероятностью 0,9973 заключена урожайность на всем массиве.
Решение. По таблице значений функции Ф(х) находим, что Ф(3) = 0.9973. Следовательно, при соотношении
 , или
, или 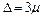
можно, зная значения m и для повторной и для бесповторной выборки, найти D (предельную ошибку выборки):
а) если выборка повторная, то
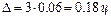 ;
;
б) если выборка бесповторная, то
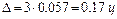 .
.
Таким образом, с вероятностью 0,9973 средняя урожайность (в ц) на всем массиве заключена в границах 15,4±0,18, т. е. от 15,4-0,18 = 15,22 до 15,4+0,18=15,58, если выборка повторная, и в границах 15,4±0,17, т. е. от 15,4-0,17=15,23 до 15,4+0,17=15,57, если выборка бесповторная.
Пример 5. Из партии, содержащей 8000 деталей, было проверено 1000 деталей. Среди них оказалось 4% нестандартных. Определить границы, в которых с вероятностью 0,9545 заключена доля нестандартных деталей во всей партии, если выборка: а) повторная, б) бесповторная.
Решение. По таблице значений функции Ф(х) находим, что 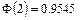 . Следовательно, приходим к равенству
. Следовательно, приходим к равенству 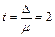 , где m — средняя квадратическая ошибка. В примере 3 (см. выше) мы вычислили, что она равна 0,0062, если выборка повторная, и 0,0059, если выборка бесповторная. Поэтому предельная ошибка выборки
, где m — средняя квадратическая ошибка. В примере 3 (см. выше) мы вычислили, что она равна 0,0062, если выборка повторная, и 0,0059, если выборка бесповторная. Поэтому предельная ошибка выборки
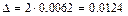 , если выборка повторная;
, если выборка повторная;
 , если выборка бесповторная,
, если выборка бесповторная,
Теперь можно найти искомые границы. Они буду таковы:
0,04±0,0124, т. е. от 0,0276 до 0,0524
(или от 2,76% до 5,24%), если выборка повторная, и
0,04±0,0118, т. е. от 0,0282 до 0,0518
(или от 2,82% до 5,18%), если выборка бесповторная.
Если требуется определить необходимый объем (п) повторной выборки, при котором с заданной надежностью (Р) отклонение выборочной средней или доли от генеральной не превысило данной предельной ошибки (D), то значение п отыскивается из соотношения 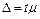 . Здесь t определяется по таблице из условия
. Здесь t определяется по таблице из условия  ,a m — по одной из четырех формул. В частности, при определении средней признака искомый объем находится в виде
,a m — по одной из четырех формул. В частности, при определении средней признака искомый объем находится в виде 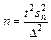 , а при определении доли признака — в виде
, а при определении доли признака — в виде 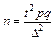 или
или 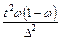 .
.
Пример 6. Из партии в 1000 единиц готовой продукции производится повторная выборка для определения доли брака. Найти тот объем этой выборки, при котором с вероятностью Р =0,99 гарантируется ошибка не свыше 0,1.
Решение. Здесь  . Значению
. Значению 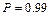 по таблице значений Ф(х) соответствует
по таблице значений Ф(х) соответствует  . При заданном
. При заданном 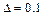 имеем
имеем  . Значение п следует найти из соотношения
. Значение п следует найти из соотношения 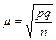 . Но в условии нет значения доли брака. Поэтому следует использовать наибольшее значение pq= 0,25. Это приводит к соотношению
. Но в условии нет значения доли брака. Поэтому следует использовать наибольшее значение pq= 0,25. Это приводит к соотношению 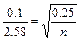 , откуда
, откуда 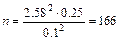 .
.
Если надо установить объем выборочной совокупности при бесповторной выборке, то из формул (3) и (4)
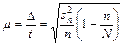 и
и 
получаются следующие выражения для этого объема в бесповторной выборке:
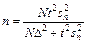 (при определении средней признака)
(при определении средней признака)
и
 (при определении доли признака).
(при определении доли признака).
Пример 7. Найти объем выборки из партии в 6000 прецизионных приборов, при котором можно с вероятностью Р= 0,890 утверждать, что отклонение доли точных приборов в выборке от вероятности их изготовления р=0,4 не превысит 0,02: а) при повторной выборке и б) при бесповторной выборке.
Решение. Здесь  дает по таблице значений Ф(х) t =1,6. Предельная ошибка выборки по условию
дает по таблице значений Ф(х) t =1,6. Предельная ошибка выборки по условию 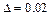 . Отсюда
. Отсюда
а) при повторной выборке применяется формула 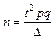 , что дает:
, что дает: 
б) при бесповторнои выборке применяем формулу  , что дает:
, что дает:
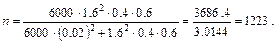
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 2807; Нарушение авторских прав?; Мы поможем в написании вашей работы!