Устойчивость выборочных средних

Применение теоремы Чебышева к выборочной средней дает возможность установить, что при достаточно большом объеме выборки выборочная средняя практически сколь угодно мало отличается от генеральной средней.

В самом деле, исходя из соответствующей этому условию формулировки следствия из теоремы Чебышева (см. п. 4.2)

,

выберем1) . Тогда вычитаемое в правой части

,

и наше неравенство преобразуется к виду

.

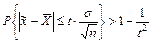При достаточно большом объеме выборки можно добиться того, чтобы не только средняя ошибка выборки 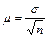2), но и t -кратная ошибка, т. е. 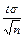, оказалась сколь угодно малой.

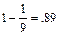Вместе с тем с увеличением t правая часть полученного неравенства быстро приближается к единице. Действительно, при t = 2 в правой части получается , при t= 3 имеем , при t = 4 имеем , при t = 5 имеем . При этом сама оцениваемая неравенством вероятность Р еще меньше отличается от единицы, чем ее граница по теореме Чебышева.

Возвращаясь к первоначальной формулировке, в которой вероятность оценивается неравенством 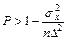, можно установить, что выполнение условия 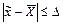при любом сколь угодно малом значении D с заданной надежностью, т. е. с вероятностью, превышающей значение правой части неравенства, может быть достигнуто только за счет увеличения n — объема выборки. Это значит, что объем N генеральной совокупности здесь не имеет существенного значения.

При этом еще установлено, что надежность достижения заданного предела отклонения выборочной средней от генеральной при данном объеме выборки возрастает, когда этот предел расширяется (см. выше изменение Р с увеличением t).

Все это показывает, что независимо от объема генеральной совокупности, а только при достаточно большом объеме случайной выборки выборочная средняя сколь угодно близка к генеральной средней. Поэтому практически совпадают выборочные средние, вычисленные для нескольких случайных повторных выборок из одной и той же совокупности, если объемы этих выборок по своей численности достаточно велики. Это указывает на устойчивость выборочных средних, что и используется в выборочном методе.

Дата добавления: 2014-12-26