Понятие о критериях согласия

Одной из задач математической статистики является отыскание закона распределения случайной величины в ее генеральной совокупности на основании известных данных (из опыта или наблюдения, т. е. из выборки) о ее значениях.

Иногда имеющиеся данные позволяют предположить, что изучаемая случайная величина подчиняется некоторому закону распределения. Тогда, вычислив значения параметров, характерных для этого закона, по имеющимся данным о значениях случайной величины мы можем записать в соответствующем виде требуемый закон распределения. Например, в случае выбора закона нормального распределения требуется подсчитать 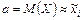и

Когда такой закон распределения построен, то возникает необходимость сопоставить данные полученного эмпирического закона с Соответствующим по теоретическому закону распределением и на основании этого сопоставления установить, подходит ли к имеющимся данным наблюдения или выборки выбранный закон распределения.

Ответ на этот вопрос находится с помощью так называемых критериев согласия.

Дадим понятие о критерии согласия Колмогорова, который связывает эмпирическую функцию распределения 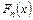1) рассматриваемой случайной величины с функцией распределения F (х) непрерывной случайной величины X.

Сущность этого критерия состоит в том, что вводят в рассмотрение функцию 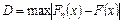. С возрастанием числа наблюдений п вероятность 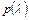неравенства 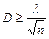стремится к своему пределу

.

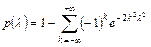Если эта вероятность велика, то расхождения между эмпирическими и теоретическими распределениями можно считать несущественными и выбранный закон подходит. При малых же вероятностях выбранный закон не подходит.

Необходимые для вывода вычисления выполняются с помощью специальных таблиц, составленных под руководством Н. В. Смирнова.

Дата добавления: 2014-12-26