Нагрузки

Геометрические размеры оси арки

При расчетном пролете l = 60 м и стреле подъема ее f = 11 м радиус арки находим по формуле

r = (l ² + 4 f ²)/(8 f) = (60² + 4×11²)/(8×11) = 46,41 м;

центральный угол дуги полуарки α определяем из выражения

cos α = (r - f)/ r = (46,41 - 11)/46,41 = 0,763,

откуда α = 40°16 '. Центральный угол дуги арки 2α = 80°32 ', длина дуги арки

S = (π r ×2α)/180° = (3,14×46,41×80,54°)/180° = 65,2 м.

Координаты точек оси арки y для вычисления моментов M находятся по формуле

,

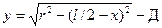где Д = r - f = 46,41 - 11 = 35,41 м и приведены в табл. 26.

Таблица 26

Координаты	Значение координат точек оси арки, м
x
y		3,69	4,9	6,47	8,51	9,91	10,73
φ	40°15 '	32°36 '	26°51 '	25°30 '	18°51 '	12°27 '	6°12 '

Постоянные расчетные нагрузки на 1 м² горизонтальной проекции покрытия определяются с введением коэффициента перегрузки n в соответствии со СНиП II-6-74, пп. 2.2. Нормативные нагрузки умножаются на коэффициент k = S / l = 64,4/60 = 1,07, учитывающий разницу между длиной дуги арки и ее проекцией.

Вес снегового покрова для III района P ₀ = 1 кН/м² горизонтальной проекции; коэффициент c ₁, учитывающий форму покрытия, в соответствии со СНиП II-6-74, табл. 5, п. 5.5 будет равен:

c ₁ = l /(8 f) = 60/(8×11) = 0,682;

тогда нормативная равномерно распределенная снеговая нагрузка

P ^н_сн = P ₀× c ₁ = 1×0,682 = 0,682 кН/м².

Собственный вес арки в зависимости от нормативного веса кровли и снега определим по формуле прил. 2

g ^н_св = (g ^н_п + P ^н_св)/[1000/(K _св l) - 1] = (0,594 + 0,682)/[1000/(4×60) - 1] = 1,276/3,16 = 0,404 кН/м².

Сбор постоянных нагрузок арочного покрытия приведен в табл. 27. Полная нормативная нагрузка от собственного веса g ^н = 0,998 кН/м² горизонтальной проекции.

Отношение нормативного собственного веса покрытия к весу снегового покрова g ^н/ P ₀ = 0,998/1 = 0,998; коэффициент перегрузки n = 1,41 (СНиП II-6-74), тогда расчетная снеговая нагрузка на 1 м² горизонтальной проекции покрытия

P ₁ = P ₀ nc ₁ = 1×1,41×0,682 = 0,962 кН/м².

Таблица 27

Наименование элемента	Нормативная нагрузка, кН/м^2	n	Расчетная нагрузка, кН/м^2
Плита покрытия
асбестоцементный лист	0,187	1,1	0,206
каркас и утеплитель	0,364	1,2	0,437
Кровля из оцинкованной стали	0,043	1,1	0,047
Арка	0,404	1,1	0,444
Подвесное оборудование	-	-	0,03
Итого	0,998	-	1,164

При снеговой нагрузке, распределенной по треугольнику, коэффициент c ₂ = (2 + 2,2)/2 = 2,1 по интерполяции и

P ₂ = P ₀ nc ₂ = 1×1,41×2,1 = 2,90 кН/м².

Расчетные нагрузки, приходящиеся на 1 м горизонтальной проекции арки при шаге арок 6 м, находятся:

от собственного веса покрытия по табл. 27

q _р = 1,164×6 = 7 кН/м;

от снега

P _1р = 0,962×6 = 5,8 кН/м;

P _2р = 2,96×6 = 17,8 кН/м.

Статический расчет арки

Схемы нагрузок показаны на рис. 43.

Расчет арки производим для следующих сочетаний нагрузок 1) постоянной и снеговой, равномерно распределенной по всему пролету; 2) постоянной по всему пролету и снеговой, равномерно распределенной на половине пролета, 3) постоянной по всему пролету и снеговой, распределенной по треугольнику на половине пролета (СНиП II-6-74, п. 5.3)

Определяем усилия в арке при разных схемах нагружения от нагрузки 10 кН/м:

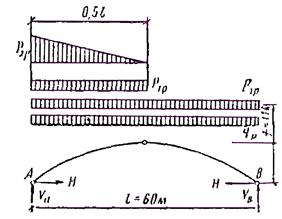
Рис. 43. Схема нагрузок от собственного веса и снега, действующих на арку

а) от равномерно распределенной нагрузки по всему пролету:

вертикальные опорные реакции

V_А = V_В = l /2 = 60/2 = 300 кН;

горизонтальный распор

H = l ²/(8 f) = 60²/(8×11) = 410 кН;

б) от равномерно распределенной нагрузки на полупролете (слева):

вертикальные опорные реакции:

V_А = 3 l /8 = 3×60/8 = 225 кН;

V_В = l /8 = 60/8 = 75 кН;

горизонтальный распор

H = l ²/(16 f) = 60²/(16×11) = 205 кН;

в) от распределенной по треугольнику нагрузки наполовине пролета (слева):

вертикальные опорные реакции

V_А = 5 l /24 = 5×60/24 = 125 кН;

V_В = l /24 = 60/24 = 25 кН;

горизонтальный распор

H = l ²/(48 f) = 60²/(48×11) = 68,2 кН.

Значения M_x, Q_x и N_x для загружения (п. а) и на участке 0 ≤ x ≤ l /2 (п. б) вычислены по формулам:

M_x = V_А × x - x ²/2 - H × y;

Q_x = - H sin φ + (V_А - x)cos φ;

N_x = H cos φ + (V_А - x)sin φ.

На участке l /2 ≤ x ≤ l - по формулам:

M_x = V_В (l - x) - Hy;

Q_x = H sin φ - V_В cos φ;

N_x = - H cos φ - V_В sin φ.

Для загружения (по п. в) вычисления проводились по формулам

на участке 0 ≤ x ≤ l /2:

M_x = V_А [ x - 3,2(l - x) x ²/ l ²] - Hy;

Q_x = V_А [1 - 4,8(l - x) x ²/ l ²]cos φ - H sin φ;

N_x = H cos φ + V_А [1 - 4,8(l - x) x ²/ l ²]sin φ;

на участке l /2 ≤ x ≤ l:

M_x = V_В (l - x) - Hy;

Q_x = H sin φ - V_В cos φ;

N_x = - H cos φ - V_В sin φ.

На рис. 44 даны эпюры изгибающих моментов от нагрузок по пп. а, б, в и от сочетания нагрузок по схемам 1, 2 и 3. На рис. 45 даны эпюры нормальных и поперечных сил от сочетания нагрузок по схемам 1, 2 и 3. Вертикальные опорные реакции V_А и V_В и распор H для различных схем загружения соответственно равны 384, 384, 523 кН (схема 1); 341, 254, 406 кН (схема 2) и 433, 255, 408 кН (схема 3).

Как видно из эпюр, расчетной является схема загружения 3 как по положительным, так и по отрицательным моментам. Максимальный положительный момент имеется в сечениях с абсциссой x = 10 м, а отрицательный - с абсциссой x = 50 м.

Дата добавления: 2014-12-26