Лабораторная работа № 6

End.

Begin

Begin

Begin

Begin

Var

Const

End.

Begin

Begin

Begin

Var

Const

End.

Begin

Begin

Begin

Var

Const

End.

Begin

Begin

Var

Const

End.

Begin

Begin

Var

Const

End.

Begin

Begin

Var

Const

Var

Var

Var

Type

Type

Теоретические сведения

МАССИВЫ

Лабораторная работа № 5

Цель работы –изучение способов описания и особенностей работы одномерных и двумерных массивов, закрепление навыков в составлении простейших разветвляющихся и циклических программ.

Постановка задачи: выполнить два задания, по одному на каждый вид массива.

Простые типы данных определяют различные множества атомарных (неразделимых) значений. Составные или структурированные типы, в отличие от простых, задают множества «сложных» значений; каждое значение из такого множества образует некоторый агрегат (совокупность) нескольких значений другого типа (или других типов). Можно сказать, что составные типы определяют некоторый способ образования новых типов из уже имеющихся, причем отдельные элементы составных значений могут иметь любой, в том числе составной, тип. Таким образом, Pascal допускает образование структур произвольной сложности, позволяя тем самым достичь адекватного представления в программе данных, с которыми она оперирует.

Одним из основных структурированных типов алгоритмических языков программирования является тип-массив. Каждое значение типа-массива состоит из фиксированного числа элементов одного и того же базового типа. Такой способ образования новых значений (фиксированное число однотипных компонент) позволяет обозначать значения этих типов одним (групповым) именем, а доступ к отдельным элементам массивов организовать посредством указания этого группового имени и индекса необходимого элемента.

Для корректного определения типа-массива необходимо задать две характеристики: тип элементов массива, а также количество и способ «нумерации» элементов. Последние характеристики задаются посредством указания типа индекса. Определение регулярного типа имеет следующий общий вид:

A: array [ t1 ] of t2;

где array и of – служебные слова, t1 обозначает тип индекса массива, t2 – тип компонент массива. В дальнейшем идентификатор этого типа может быть использован в описании переменных.

В качестве типа индекса может выступать любой дискретный тип, кроме Longint и ограниченных типов, построенных из типа Longint; в частности, допустимы перечислимые и ограниченные типы. Элементами массива могут быть значения любого типа.

Ниже приведены несколько примеров описания массивов.

M1 = array [1..100] of real;

M2 = array [char] of boolean;

Matrix = array [1..10] of array [1..20] of integer;

Vector: M1;

Sym_Table: M2;

Arr1,Arr2: Matrix;

Следует подчеркнуть некоторые различия между массивами в языке Pascal и в некоторых других языках программирования.

Во-первых, в Pascal количество элементов массива всегда должно быть фиксированным, то есть определяться при трансляции программы. Это считается определенным недостатком языка, так как не во всех программах можно зарнее предсказать необходимый размер массива (который может определяться в зависимости от тех или иных условий, возникающих в процессе исполнения).

Для задания количества элементов массива используется имя типа; число элементов определяется количеством возможных значений указанного типа, что отличает Pascal от многих других языков, в которых размер массива задается либо целым числом (или выражением целого типа), либо диапазоном целых чисел. Такая особенность языка Pascal придает ему дополнительную гибкость, позволяя “нумеровать” элементы массива не только целыми числами, но и значениями произвольного дискретного типа. Например, массив Sym_Table из предыдущего примера может адекватно моделировать некоторую логическую шкалу, в которой каждому символу (с типом char) соответствует некоторое логическое значение, а доступ к элементам этого массива может быть организован следующим образом:

Sym_Table [‘a’]:= true;

If Sym_Table [‘.’] then …;

В качестве элементов массива могут выступать значения любого типа, в частности, ими могут быть значения любых составных типов, например массивы:

V2: array [1..10] of array [1..20] of byte;

Такую переменную можно трактовать двояко: либо как массив, состоящий из нескольких массивов, либо как один двумерный массив (матрица). Для сокращения записи в подобных случаях можно использовать эквивалентную форму определения регулярных типов, где в квадратных скобках указывается список типов индексов, разделенных запятыми, например:

V2: array [1..10,1..20] of byte;

Количество индексов в определении (то есть размерность массива) в языке не ограничивается.

Pascal допускает единственно возможное действие над массивом в целом: использование его в операторе присваивания, например:

Vect1:=Vect2;

причем оба массива в данном случае должны иметь идентичный тип.

Доступ к элементам массива строится традиционно: после идентификатора массива в квадратных скобках указывается индекс нужного элемента или список индексов, определяющий элемент многомерного массива. В качестве индексов могут выступать произвольные выражения, тип которых должен соответствовать типу индексов в описании массива.

Так, доступ к элементам массива, описанного в первом примере, строится следующим образом:

Vector[1];

Vector[(i+1)*2].

Двумерный массив V2, описанный выше, допускает такой доступ к своим элементам:

V2[3,7]

V2[i,j]

Рассмотрим подробнее массив V2. Вследствие того, что его можно трактовать как «массив массивов», то, например, конструкция V2[ k ] вполне допустима в языке и в данном случае обозначает k –й массив в группе из 10 массивов байтовых элементов. Для того чтобы адресоваться, скажем, к 5-му элементу этого массива, можно записать V2[ k ][5].

Такая запись корректна, но ее более привычный эквивалент – V2[ k,5] – можно считать сокращением первоначальной записи.

Элемент массива считается переменной (индексированной); он может получать значения (например, в операторе присваивания), а также участвовать в выражениях, где он представляет значение, помещенное в соответствующий элемент данного массива. Ассортимент операций над элементами массива полностью определяется типом этих элементов (базовым типом массива).

Рассмотрим примеры решения некоторых типовых задач, связанных с обработкой массивов.

1. Упорядочивание массива по возрастанию.

Упорядочивание массива по какому-либо признаку называется сортировкой. Существуют различные методы сортировки, они различаются в основном по скорости получения результата. Рассмотрим один из них – метод “пузырька”. Это наиболее простой (но и наиболее медленный) метод сортировки. Его еще называют «сортировка обменом пар».

Рассмотрим алгоритм этого метода подробно. Пусть имеется последовательность из шести чисел, содержащих следующие значения: 1, 3, 4, 2, 6, 5.

Пройдем по массиву, сравнивая первый элемент со вторым, второй с третьим и так далее до пятого. Будем проверять упорядоченность, и если она нарушена (т.е. если значение некоторого элемента больше значения следующего элемента), то поменяем эти значения местами. Например, дойдя до третьего элемента, значение которого равно 4, мы обнаружим, что оно больше значения четвертого элемента, равного 2. Выполнив обмен, получим новую последовательность значений: 1, 3, 2, 4, 6, 5.

После этого перейдем к четвертому элементу. Теперь его значение равно 4. Значение следующего элемента равно 6, оно больше 4, поэтому обмена значениями не происходит. Перейдя к пятому, обнаруживаем, что его значение больше шестого, и производим обмен. Итак, выполнив один проход по массиву, получим последовательность значений: 1, 3, 2, 4, 5, 6.

Эта последовательность до конца не отсортирована. Однако мы можем с уверенностью сказать, что наибольший элемент находится на своем месте – на правой границе массива. Выполняя новые проходы, каждый раз сокращая количество просматриваемых элементов на 1, мы в конечном счете отсортируем все значения. Данный алгоритм получил название «пузырьковая сортировка», так как в процессе каждого прохода элемент как бы «всплывает» на свое место, подобно пузырьку воздуха в воде.

Приведем пример программы, реализующей описанный алгоритм сортировки.

Program sort;

n=7;

a: array [1..n] of real;

x,i,j:integer;

For i:=1 to n do

write(‘a[‘,i,’]=’);

readln(a[i]);

end;

For i:=1 to n-1 do

For j:=1 to n-i do

If a[j]>a[j+1] then

Begin

x:=a[j];

a[j]:=a[j+1];

a[j+1]:=x

end;

For i:=1 to n do

write(a[i]:5);

readln;

2. Поиск элемента в массиве.

Одна из важных невычислительных задач – поиск данного значения среди элементов массива. Такой поиск также называется поиском по ключу. На практике поиск осуществляется в упорядоченном массиве. Имеются различные алгоритмы поиска. В данном учебном примере осуществим поиск путем сплошного перебора. Если элемент найден, напечатаем его номер, если нет – выдадим соответствующее сообщение. Существенным является то, какой из одинаковых элементов массива, равных данному, нас интересует: первый, встретившийся при поиске, или последний. В данном примере будем искать первый. Поиск осуществляется в цикле. Как только элемент найден, надо выйти из цикла. Для досрочного выхода из цикла используем оператор безусловного перехода goto. Если досрочный выход не произойдет, значит, элемент, равный данному, в массиве отсутствует. В таком случае выдача сообщения об отсутствии элемента должна быть сразу после цикла поиска. Следовательно, чтобы обойти печать номера элемента, надо использовать еще один оператор goto и еще одну метку в программе.

Возможный вариант программы поиска:

Program poisk;

n=7;

label 1,2;

a: array [1..n] of real;

x:real;i:integer;

For i:=1 to n do

write(‘a[‘,i,’]=’);

readln(a[i]);

end;

write(‘введите искомое x=’);

readln(x);

For i:=1 to n do

If a[i]=x then goto 1;

writeln(‘такого числа в массиве нет’);

goto 2;

1: write(‘номер элемента массива, равного данному значению ’,i)

3.Алгоритмы обработки матриц.

Двумерный массив или прямоугольная матрица B из n строк и m столбцов в общем виде выглядит следующим образом:

b₁₁ b₁₂ b_1m

b₂₁ b₂₂ b_2m

b_n1 b_n2 b_nm

На языке Pascal имена элементов массива записываются также с двумя номерами (индексами):

b[1,1],b[1,2],…,b[1,m],b[2,1],b[2,2],…,b[2,m],…,b[n,1],b[n,2],…,b[n,m].

В памяти компьютера элементы двумерного массива расположены один за другим: после элементов первой строки следуют элементы второй строки матрицы и т.д. Если количество строк матрицы равно количеству столбцов, то такая матрица называется квадратной. Главная диагональ квадратной матрицы проходит из левого верхнего угла в правый нижний.

Рассмотрим задачи обработки матриц и алгоритмы их решения.

3.1. Вычисление суммы элементов главной диагонали квадратной матрицы.

Для решения задачи надо выполнить следующие шаги: ввести матрицу в память; найти сумму элементов главной диагонали; напечатать результат. Описание матрицы, как и описание одномерного массива, используется для резервирования памяти. В описании матрицы указываются диапазоны для двух номеров: строк и столбцов.

При обработке массивов в разделе описания переменных программы появляются имена индексов элементов: для одномерных массивов – одной, для двумерного – двух целочисленных переменных.

При вычислении суммы элементов диагонали следует обратить внимание на имена суммируемых элементов: оба индекса имеют одинаковое значение, т.е. в общем виде имя элемента диагонали будет b[i,i]. Это означает, что можно рассматривать диагональ как одномерный массив и использовать один цикл для вычислений.

Программа имеет следующий вид:

Program Sum_Diagonal;

N=3;

b: array [1..n,1..n] of real;

I,j:interger;

S:real;

writeln(‘введите значения элементов матрицы по строкам’);

writeln(‘в конце каждой строки нажимайте Enter’);

for i:=1 to n do

for j:=1 to n do read(b[i,j]);

writeln;

end;

S:=0;

for i:=1 to n do

S:=s+b[i,i];

write(‘сумма элементов диагонали матрицы s=’,s);

3.2.Нахождение наибольших элементов каждой строки матрицы.

Каждую строку матрицы можно рассматривать как одномерный массив и использовать идею нахождения наибольшего значения в программе maxim из предыдущего раздела. Найденные значения будем помещать в одномерный массив a.

Program Max_In_Rows;

n=3;

b: array [1..n,1..n] of real;

I,j:interger;

a: array [1..n] of real;

writeln(‘введите значения элементов матрицы по строкам’);

writeln(‘в конце каждой строки нажимайте Enter’);

for i:=1 to n do

for j:=1 to n do read(b[i,j]);

writeln;

end;

for i:=1 to n do

a[i]:=b[i,1];

for j:=2 to n do

if a[i]<b[i,j] then a[i]:=b[i,j];

end;

writeln (‘Наибольшие значения строк матрицы S’);

writeln (‘Номер строки Наибольшее значение’);

for i:=1 to n do

writeln (i:6,’ ’:20,a[i]);

3.3. Нахождение сумм элементов столбцов матрицы.

При обработке матриц можно осуществлять операции как над строками, так и над столбцами. При нахождении суммы элементов столбцов можно использовать алгоритм из программы summa предыдущего раздела. Для лучшего понимания работы программы введем переменную S для вычисления суммы, а затем для каждого столбца запишем полученный результат в массив a, т.е. присвоим его переменной a[j], где j – текущий номер столбца матрицы.

Ниже приводится возможный вариант программы.

Program Sum_By_Columns;

n=3;

b: array [1..n,1..n] of real;

I,j:interger;

S:=real;

a: array [1..n] of real;

writeln(‘введите значения элементов матрицы по строкам’);

writeln(‘в конце каждой строки нажимайте Enter’);

for i:=1 to n do

for j:=1 to n do read(b[i,j]);

writeln;

end;

for j:=1 to n do

S:=0;

for i:=1 to n do S:=S+b[i,j];

a[,j]:=S;

end;

write(‘сумма элементов столбцов матрицы: ’);

for i:=1 to n do

write(a[i]);

3.4. Перестановка строк матрицы.

В прямоугольной матрице b из n строк и m столбцов требуется поменять местами две строки. При решении этой задачи можно использовать алгоритм обмена значениями двух переменных из программы сортировки. Для этого достаточно организовать цикл по переменной столбца и, используя промежуточную (буферную) переменную, менять местами каждую пару элементов, стоящих в одном столбце. При заданных номерах строк K и L решение выглядит так:

Program Sum_Diagonal;

n=3;m=4;

b: array [1..n,1..m] of real;

c:real;

K,L,i,j:interger;

write(‘Введите номера меняемых местами строк матрицы’);

readln(K,L);

writeln(‘введите значения элементов матрицы по строкам’);

writeln(‘в конце каждой строки нажимайте Enter’);

for i:=1 to n do

for j:=1 to n do read(b[i,j]);

writeln;

end;

for j:=1 to m do

c:=b[K,j];

b[K,j}:=b[L,j};

b[L,j}:=c;

end;

writeln;

writeln(‘матрица с переставленными строками:’);

for i:=1 to n do

for j:=1 to m do

write(b[i,j]);

wtiteln

end;

Пример решения лабораторной работы.

Задача 1. Рассчитать сумму отрицательных элементов массива А(n), если известно, что n = 5, A = (1.5, -4.6, 10, -1.7, -4.9).

Программа 1:

PROGRAM lab5_1;

CONST

n=5;

TYPE

ar=array[1..n] of real;

VAR

a:ar;

s:real;

i:integer;

BEGIN

{Ввод исходных данных}

WriteLn(‘Введите ’, n, ' вещественных элементов массива‘);

for i:=1 to n do

Read(a[i]);

{Выполнение задачи}

s:=0;

for i:=1 to n do

if a[i]<0 then s:=s+a[i];

{Вывод результата}

if s=0 then WriteLn(‘Отрицательных элементов нет.’)

else WriteLn(' S=',s:8:4);

END.

Результаты расчета:

S=-11.2000

Задача 2. Найти разность R между максимальным и минимальным элементами массива

Программа 2:

PROGRAM lab;

CONST

m=3; {количество строк, столбцов}

TYPE

mas=array[1..m,1..m] of integer;

VAR

A:mas; {массив А}

R:integer; {разность}

Amax:integer; {максимальный элемент}

Amin:integer; {минимальный элемент}

i,j:integer; {счетчики по строкам, столбцам}

BEGIN

for i:=1 to m do {чтение исходных данных}

for j:=1 to m do read(A[i,j]);

close(fi)

Amin:=A[1,1]; {начальные установки}

Amax:=A[1,1];

for i:=1 to m do {поиск минимального и максимального элементов} for j:=1 to m do

begin

if A[i,j]<Amin then Amin:=A[i,j];

if A[i,j]>Amax then Amax:=A[i,j]

end;

R:=Amax-Amin; {разность}

WriteLn(' R=',R:4);

close(fo)

END.

Результаты расчета:

R = 20

Варианты заданий

Задача 1

1. Найти корни уравнения Ax + Bsina = 0, где a = 1.3, A = {1.1, 2.5, 3.9, 8.1, 4.5, 12.1, 11.9, 15.5}. (i = 1..8).

2. Вычислить массив , где – положительные корни уравнения Ax + Bcosb = 0, при А = 0.75, B = 4.5, b = -1.5.. 2.5, .

3. Найти сумму всех положительных элементов массива A = {-1.2, 3.5, 4.1, 8.5, 5.3, -6.1, 3.4, 2.7}.

4. Найти произведение элементов массива A = {1, 3.5, 4, -0.8, 1.9, 5, 13}, удовлетворяющих условию , если С = 2, D = 10. Сформировать из этих элементов массив Z.

5. Вычислить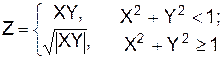

при Y = -5.5, X = {-1.8, -1.6,..., 1.2}. Результат представить в виде массива.

6. Найти номера первого нечетного и последнего четного чисел из последовательности целых чисел N = {10, 8, 4, 3, 6, 15, 2}.

7. Даны два массива: A = {1.1, 2, 4, 5.1, -8.2, -1.5, 1.2}, B = {-1.3, 2.7, -3.2, 5, 1.8, -4.6, -1.2}. Найти число перемен знаков последовательности попарных произведений

8. Найти разность между максимальным и К-м элементом массива А = {-1.1, 2.5, -2.9, 8.8, 14.5, 2.2, -1.3, 5.9} при К = 4.

9. Вычислить элементы массива

где x – корни серии уравнений Аx + sini = 0, , А = 5.5.

10. Найти сумму первых К положительных элементов массива А = (2.8, -3.5, -2.1, 4, 6, 8.1, 6.2, 9.5, 1.1) при К = 5.

11. Найти количество элементов массива A = {1.2, 5, 7, 9.3, 6.9, -8, -1.5, 2.5, 2.8}, удовлетворяющих условию , если С = -3.5, D = 6. Сформировать из этих элементов массив F.

12. Найти произведение последних N отрицательных элементов массива А = (-5, 6.1, -9.2, 4, 5, -2, 7, -1, 5, 4, 1.9, -3, 5); N = 3.

13. Сформировать массив , четные компоненты которого равны компонентам массива А = (-5.1, 2.3, 4.6, 5.8, -2.9), нечетные – компонентам массива В = (2.8, 3, 5.4, -1.9, -4.1).

14. Найти количество положительных, отрицательных и равных нулю элементов массива М = (-5, 0.1, 2.8, 0.64, 3, -5.1, 0, -7.5, 4.6, 10).

15. Среди последовательности чисел 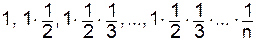найти первое, меньшее заданного числа e (e = ).

16. Элементы массива A вычисляются по формуле 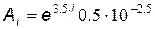, i = 1..10. Сформировать массив B, элементы которого удовлетворяют условию , если С = 2.5, D = 10.3.

17. Задан массив целых чисел N = (1, 5, -3, 3, 15, 21, 8, -5). Необходимо за один просмотр найти два минимальных числа.

18. Вычислить значения элементов массива S, которые являются модулями элементов массива Z: .

19. Даны два массива: М1 = (-5, 10, 21, 35, -9, 11, 4, 5) и М2 = (1, 5, 10, -3, 4, -15, 36, 6, 11). Найти их объединение и результат записать в массив М3.

20. Вычислить где х = , массив, элементы которого являются остатком от деления целых компонентов массива N = (156, 18, 72, 10, 95, 100) на целое число К = 9.

21. Задан массив Х = (-1.5, 6.8, -3, 9, 7, -2.7, -4.5, 1.6). Вычислить произведение модулей отрицательных и сумму положительных элементов массива Х.

22. Заданы массивы А = (-1.1, 2, 8, 9, 5, 5.3, 5, -5, 2.1) и С = (8, 9, 1, 2, -5, 3.4, 4.9, 6, 1.8). Найти их пересечение и результат записать в массив В.

23. Задан массив А = (5.5, -6, 8, 9.1, -3.5, 4.1, 10, -1, 2.5). Вычислить , где и – соответственно максимальный и минимальный элементы массива А; – их среднее арифметическое.

24. В массиве Н = (-0.5, 2.8, 9.1, -0.3, 10, -1, 2.1, 8.2) указать номер первого элемента, сумма которого с последующим за ним элементом не превышает D (D = 1.5).

25. Вычислить

где – элементы массива В = (0.1, 2, 5, -3.1, 4.2, -1.2, 6, -2, 3.7, 5.2), n = 10, a = 4.5.

26. Решить квадратное уравнение , где А – сумма элементов массива К = (2.1, 0.25, 1.4, -1.9), В – их произведение, а С = -1.34.

27. Вычислить элементы массива Y по формуле

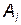где - корень уравнения , – элемент массива А = (1.2, -4.6, 3.8, -2.3, 0.6, 1.7).

28. Найти большее из чисел А, В, С, где А – сумма модулей отрицательных, В – произведение положительных элементов массива К, С – разность между максимальным и минимальным его элементами. К = (10.1, 0.2, -3.4, -0.5, 3.6, -12.9, 5.7).

29. Определить произведение двух чисел А×В, где А – сумма первых К, а В – последних К элементов массива С = (2, 4, -2, 9, 7, -10, 11, -1), К = 3.

30. Определить величины и индексы максимального по модулю и минимального элементов массива В = (-1.5, 6.9, 13, 6.2, -17, 8, 6.6).

Задача 2

1. Задан массив А(m,n). Сформировать массив В из наименьших элементов каждой строки массива А:

2. Дан массив В(m,n). Сформировать массив С(n) из сумм элементов каждого столбца В:

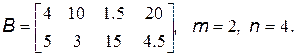
3. В массиве Е(m,n) поменять местами элементы i-й и k-й строк:

4. В массиве Р(m,n) все элементы разделить на максимальный элемент k-го столбца:

5. Задан массив А(m,n). Сформировать массив С из элементов четных столбцов и массив В из элементов нечетных строк массива А:

6. Дан целочисленный массив О(m,n). Сформировать одномерные массивы В и С, содержащие, соответственно, четные и нечетные элементы массива А:

7. Сформировать массив В из произведений элементов столбцов массива Z:

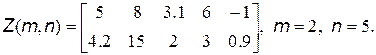
8. Сформировать массив Т из сумм элементов, расположенных в строках с отрицательными элементами на главной диагонали исходного массива Z:

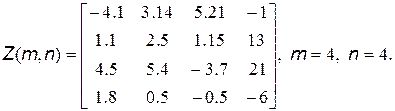
9. Сформировать массив NS из номеров строк массива R, в которых имеются повторяющиеся значения:

10. В массиве Q(m,n) заменить отрицательные элементы номером столбца, в котором они находятся:

11. Сформировать массив В из элементов массива А, меньших Е:

12. Сформировать массив В из элементов, расположенных ниже главной диагонали исходного массива К:

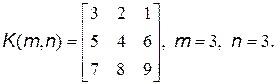
13. В массиве V(n,n) элементы строки, содержащей наибольший элемент, заменить на s:

14. Преобразовать массив H(n,n), разделив все элементы на максимальный элемент К-го столбца:

15. Найти разность R между максимальным и минимальным элементами массива W:

16. Задан массив A(m,n). Сформировать массив B из положительных элементов массива A:

, m = 2, n = 3.

17. Преобразовать массив G(m,n), поменяв местами элементы К-го и (К+1)-го столбцов:

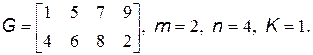
18. К отрицательным элементам массива D(m,n) прибавить S, а из положительных вычесть X:

19. В массиве F(n,m) заменить все положительные элементы их квадратами, а отрицательные – их кубами:

20. Сформировать массив В из отношений элементов N и S столбцов массива:

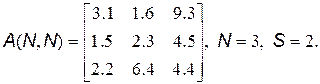
21. Сформировать массив R из номеров строк массива Y(m,n), в которых находятся максимальные элементы каждого столбца:

22. Сформировать массив К из положительных отношений элементов n-го и s-го столбцов массива

23. Сформировать одномерный массив В из элементов массива А(n,n), которые по величине больше, чем С:

24. Элементы массива S(m,m) разделить на сумму элементов, расположенных на главной диагонали:

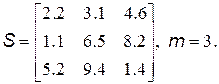
25. Преобразовать массив А(m,n), умножив его элементы на сумму соответствующих им индексов:

26. Сформировать массив В из элементов главной диагонали и массив С из элементов дополнительной диагонали исходного массива А:

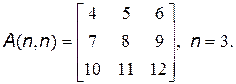
27. Определить сумму S элементов массива А(n,n), расположенных ниже главной диагонали, и произведение Р элементов массива А(n,n), расположенных выше главной диагонали:

28. Преобразовать массив К(m,m), заменив все элементы, большие А, максимальным элементом массива К, а элементы, меньшие В, – минимальным его элементом:

29. Определить массив В из произведений элементов строк исходного массива K:

30. Найти разность R между максимальным и минимальным элементами массива Y:

Дата добавления: 2014-12-26