Вывод коэффициента рекуррентности q

Repeat

Repeat

Begin

End.

Begin

Begin

Var

End.

Begin

Var

p,x: real;

i,n: integer;

read(x,n);{ввод x,n}

p:=1;{присвоение степени начального значения}

for i:=1 to abs(n) do

p:=p*x;{вычисление степени}

if n<0 then {если степень отрицательна}

p:=p/x;

write(p);

Оператор цикла с предусловием используется в тех случаях, когда количество повторений цикла заранее не известно. Он имеет следующую синтаксическую форму:

while < условие > do < оператор >;

Этот оператор задает повторяющееся выполнение оператора, содержащегося в нем. Перед каждым выполнением внутреннего оператора производится проверка значения булевского выражения (условие), которое служит критерием повторения: если это выражение имеет значение true, то выполняется очередная итерация; в противном случае выполнение оператора цикла заканчивается. Если выражение с самого начала имеет значение false, то цикл не выполнится ни разу.

Предположим, нужно подсчитать количество цифр целого положительного десятичного числа. Программа решения этой задачи может выглядеть следующим образом:

Program digits;

n,k: integer;

write(‘введите n’);

readln(n);

k:=1;

while n div 10>0 do

k:=k+1;

n:=n div 10;

end;

write(‘Количество цифр:’,k);

У этой программы есть один недостаток: она не обрабатывает отрицательные числа. По условию от нее этого и не требуется. Однако пользователь может ввести и отрицательное число. Перепишем программу так, чтобы пользователь вводил число до тех пор, пока оно не будет положительным. Фрагмент ввода будет теперь выглядеть следующим образом:

write(‘введите положительное n’);

readln(n);

while n < 0 do

write(‘введите n’);

readln(n);

end;

Это простой пример так называемой защиты от дурака. Теперь пользователь не получит результат, пока не введет положительное число. Однако нам пришлось написать один и тот же фрагмент ввода числа дважды: перед циклом и в теле цикла. Поэтому здесь лучше воспользоваться другим оператором цикла, а именно оператором цикла с постусловием.

Оператор цикла с постусловием имеет следующую синтаксическую форму:

оператор1;

оператор2;

......

операторN;

until <условие>;

Этот оператор аналогичен предыдущему. Отличие заключается в том, что условие окончания цикла проверяется после выполнения очередной итерации (таким образом гарантируется хотя бы однократное выполнение цикла). Кроме того, критерием окончания цикла является равенство выражения, описывающего <условие>, константе true. Если выражение имеет значение false, то цикл выполняется.

Перепишем теперь фрагмент ввода, используя цикл repeat.

write(‘введите положительное n’);

readln(n);

until n>=0;

Классическим примером задачи на применение цикла с условием является вычисление суммы членов степенного ряда. Пусть необходимо вычислить

_.

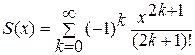Для любого k было бы нерационально считать входящие в выражения для общего члена степень и факториал с самого начала, имея их значения при предыдущем k. Как степень, так и факториал будут возрастать с ростом k, что может привести к потере точности и/или переполнению разрядной сетки при раздельном их вычислении. Удобнее найти так называемое рекуррентное соотношение, которое устанавливает зависимость между двумя соседними членами ряда в виде коэффициента рекуррентности (q) и в дальнейшем вычислять рекуррентно b_k = b_k–1q для k = 1, 2,... при очевидном начальном условии b₀ = x. Для нашего случая

.

Пример выполнения задания

;

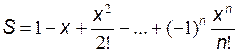1) n = 9, x = 0.6;

2) x = 0.1…1.0,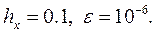

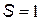до цикла

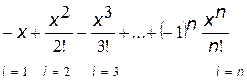цикл ®

.

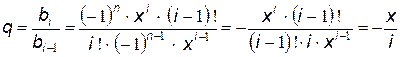Проверка правильности вычисления q

До цикла: предыдущее слагаемое ;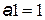

Значение переменной .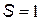

Цикл начинается при значении переменной 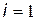и заканчивается при .

		–
		–
		–
: :	: :	: :	: :	: :
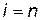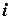
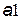
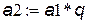
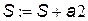
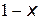
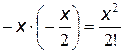
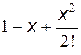
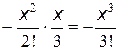
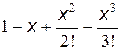
n		–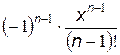

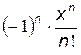
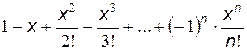
Программа для задачи 1:

PROGRAM lab7_1;

uses crt;

CONST n=9; { количество элементов суммы }

x=0.6; { для этого Х вычислить сумму }

VAR s:real; { искомая сумма }

q:real; { коэффициент рекуррентности }

a1,a2:real; { предыдущий и следующий элементы суммы }

i:integer; { счетчик элементов суммы }

BEGIN

clrscr; { очистка экрана }

s:=1; { значение суммы до начала цикла }

a1:=1; { слагаемое непосредственно перед началом цикла}

FOR i:=1 TO n DO

begin

q:=-x/i; { i-й коэффициент рекуррентности }

a2:=a1*q; { следующий элемент суммы }

s:=s+a2; { суммирование }

a1:=a2 { "переброс" – подготовка к следующему такту цикла}

end;

writeln;

writeln (' x=',x:5:1,' s=',s:9:6);

readln;

END.

Экран выполнения программы для задачи 1:

Программа для задачи 2:

PROGRAM lab_7_2;

USES crt;

CONST xn=0.1; { начальное значение Х }

xk=1.0; { конечное значение Х }

hx=0.1; { шаг по Х }

eps=1e-6; { точность вычисления суммы }

VAR S:real; { сумма }

q:real; { коэффициент рекуррентности }

a1,a2:real; { предыдущий и следующий элементы суммы }

x:real; { текущее значение Х }

i:integer; { счетчик элементов суммы }

k:integer; { счетчик количества точек Х }

BEGIN

clrscr; { очистка экрана }

x:=xn; { начальная точка Х }

k:=1; { номер точки X }

WHILE x<=xk+eps DO { начало цикла по Х }

BEGIN

s:=1; { значение суммы до цикла в К-й точке Х }

a1:=1; { слагаемое непосредственно перед началом цикла}

i:=1; { начальное значение счетчика i }

REPEAT {цикл REPEAT для вычисления суммы в К-й точке Х}

q:=-x/i;

a2:=a1*q;

s:=s+a2;

i:=i+1;

a1:=a2

UNTIL abs(a2)<eps; { закончился оператор REPEAT }

writeln;

writeln (k:2,'. ',' x=',x:3:1,' s=',s:9:6);

k:=k+1;

x:=x+hx; { переход на следующий Х }

END; { закончился оператор WHILE }

repeat until keypressed; { задержка экрана }

END.

Экран выполнения программы для задачи 2:

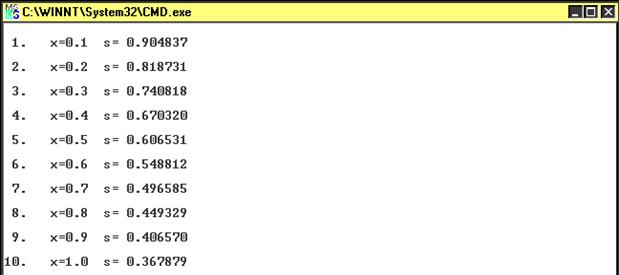
Варианты заданий

1. ;

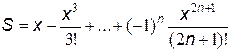1) n = 6, x = 0.1; 2) x = 0.1…1.0,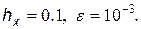

2. ;

1) n = 8, x = 1.2; 2) x = 1…2,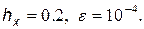

3.

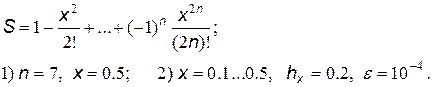
4.

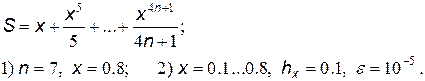
5.

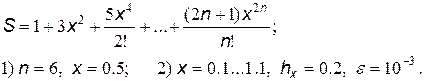
6.

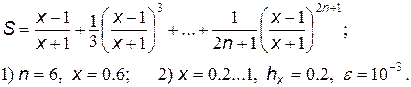
7.

8.

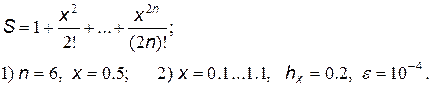
9.

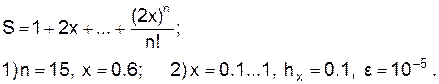
10.

11.

12.

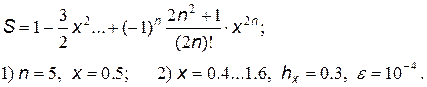
13.

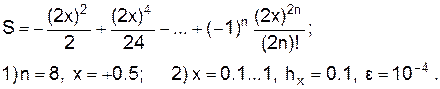
14.

15.

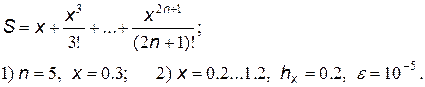
16.

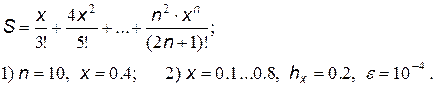
17.

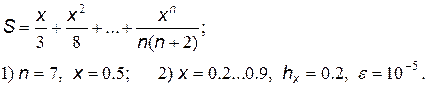
18.

19.

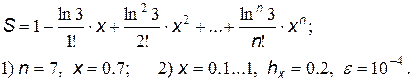
20.

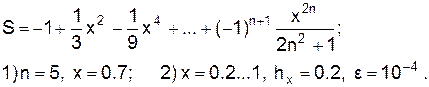
21.

22.

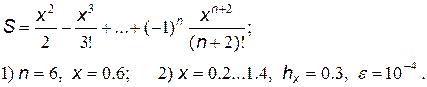
23.

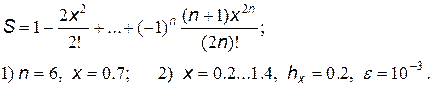
24.

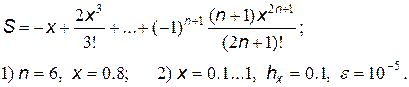
25.

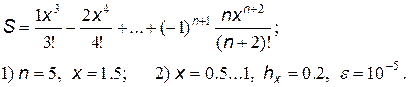
26.

27.

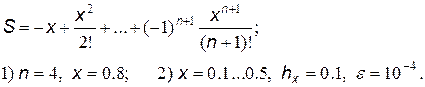
28.

29.

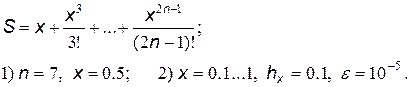
30.

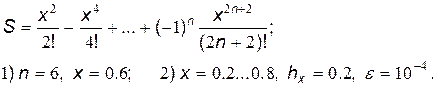
Дата добавления: 2014-12-26