Определение нелинейных составляющих для корпуса

Методика расчёта нелинейных составляющих для корпуса строится по аналогии с нестационарным двумерным течением [3,10]. Аналогия вихреобразования над корпусом при больших углах атаки и за цилиндром, мгновенно приведенным в движение из состояния покоя, позволяет вместо стационарного трёхмерного обтекания корпуса рассматривать в функции времени стационарное двухмерное обтекание цилиндра. Отсюда [10]

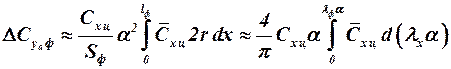, (4.8)

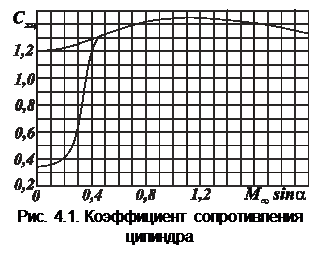
где – коэффициент сопротивления цилиндра при установившемся поперечном обтекании со скоростью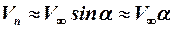
(рис. 4.1).

При дозвуковых скоростях величина коэффициента зависит от структуры пограничного слоя. Учитывая тот факт, что при дозвуковых скоростях возможно наличие смешанного пограничного слоя, в первом приближении можно принимать в этом диапазоне чисел .

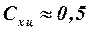После аппроксимации интеграла в (4.8) линейной зависимостью получается следующая приближённая формула для определения нелинейной составляющей подъёмной силы изолированного корпуса:

. (4.9)

Аналогичным образом можно получить формулу для продольного момента от этой составляющей:

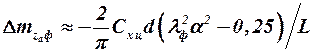, (4.10)

где 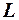– характерный размер.

Из формул (4.9) и (4.10) можно получить

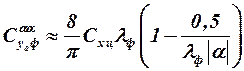, (4.11)

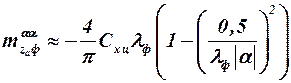. (4.12)

Следует иметь в виду, что при углах атаки 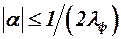нелинейная составляющая подъёмной силы корпуса принимается равной нулю, поэтому и величины, вычисляемые по формулам (4.9) – (4.12), должны быть также равны нулю.

Дата добавления: 2014-12-26