Скос потока в районе вторых несущих поверхностей

Вторые несущие поверхности находятся в аэродинамическом следе от впереди расположенных частей ЛА, что приводит к изменению скоростного напора и действительного угла атаки. С впереди расположенных частей ЛА обычно сходит довольно сложная вихревая структура. Она зависит от угла атаки 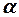, числа , геометрических параметров впереди расположенной несущей поверхности, а также от интерференции между ней и корпусом. Определить форму этой структуры довольно трудно, поэтому точное решение общей задачи представляет почти непреодолимые затруднения. Задача усложняется ещё более в связи с тем, что при определённых условиях эта структура является нестационарной, т. е. неустойчивой.

Поэтому для получения хотя бы некоторых качественных выводов общего характера оказывается целесообразным применить для описания этих сложных явлений более простую математическую модель. Задача значительно упрощается, если рассматривать эти явления при очень малых по модулю углах атаки. Изменение скоростного напора при этом учитывается введением коэффициента торможения 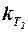, определяемого в соответствии с подразд. 2.2.5. Так как вторые несущие поверхности находятся на сравнительно большом расстоянии вниз по потоку от впереди расположенных поверхностей, то сходящую с впереди расположенных частей ЛА вихревую структуру удаётся смоделировать в этой области очень простой моделью.

Рассматривая обтекание дозвуковыми скоростями нестреловидного крыла большого удлинения при малых по модулю значениях угла атаки, можно отметить, что сходящая с крыла вихревая пелена непосредственно за крылом начинает сворачиваться в районе боковых кромок в два отчётливо различимых вихревых шнура, имеющих одинаковые, но противоположные по знаку значения циркуляции.

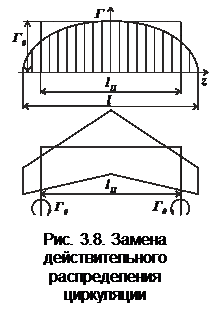Поскольку вторые несущие поверхности располагаются на некотором расстоянии от задних кромок впереди расположенной поверхности, то допустимо для определения скоса потока в этом районе вихревую пелену первой поверхности «заменить» присоединённым вихрем постоянной интенсивности, ось которого располагается вдоль геометрического места фокусов профилей в сечениях крыла, а с концов направляются по потоку два свободных вихря. Так как составляющие скорости от «перекладины» вдали от неё значительно меньше этих составляющих от боковых вихрей, то вполне допустимо для крыльев произвольной формы в плане разместить её в фокусе несущей поверхности и направить перпендикулярно вектору скорости (рис. 3.8). Такая идеализация явления – переход к так называемому П -образному вихрю – соответствует предельно простому представлению вихревой системы.

Интенсивность циркуляции 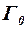П -образного вихря равна циркуляции в корневом (бортовом) сечении несущей поверхности. Поэтому из условия равенства суммарной циркуляции определяем расстояние между свободными вихрями :

.

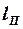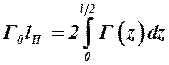Величина относительного размаха П -образного вихря 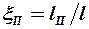зависит только от распределения циркуляции по размаху несущей поверхности. Например, при эллиптическом законе распределения циркуляции 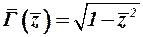величина 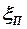будет равна 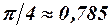, а при линейном законе 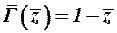– 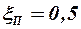. Здесь 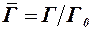, , 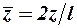где – размах несущей поверхности.

При положительном угле атаки эта вихревая структура создаёт профиль вертикальных скоростей, уменьшающий угол атаки при 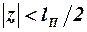и увеличивающий его при .

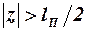Определение скоса потока при сверхзвуковых скоростях полёта имеет ряд особенностей, связанных как непосредственно с обтеканием, так и с наличием областей влияния.

Известно, что при дозвуковых скоростях непосредственно за задней кромкой симметричного профиля (крыла бесконечного размаха) скос потока будет равен углу атаки. При удалении от профиля угол скоса по модулю уменьшается. Это приближённо моделируется «перекладиной». При сверхзвуковых скоростях скос за задней кромкой симметричного профиля очень мал (считается, что угол скоса 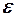приблизительно пропорционален 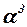(углы в радианах); по линейной теории он принимается равным нулю). Поэтому при сверхзвуковых скоростях за прямоугольным крылом существует целая область, где скос потока практически отсутствует (пока эта область будет находиться вне зоны влияния боковых вихрей). Здесь вихревая пелена моделируется только боковыми вихрями (без «перекладины»). Следует отметить, что для этого крыла интенсивность боковых вихрей очень сильно зависит от угла «среза» боковых кромок. Если «срез» боковых кромок делает их сверхзвуковыми, то скос потока за таким крылом будет практически отсутствовать. Величина скоса потока также будет сильно отличаться и за треугольным крылом в зависимости от того, какими являются передние кромки – дозвуковыми или сверхзвуковыми. Однако, несмотря на очень большое количество недостатков, эта простая модель П -образного вихря позволяет в большинстве случаев получать не противоречащий истине результат.

В общем случае на величину 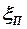оказывают влияние те же параметры, от которых зависит распределение циркуляции по размаху несущей поверхности, т. е.

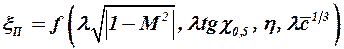. (3.48)

Графики этих зависимостей приведены на рис. 3.9.

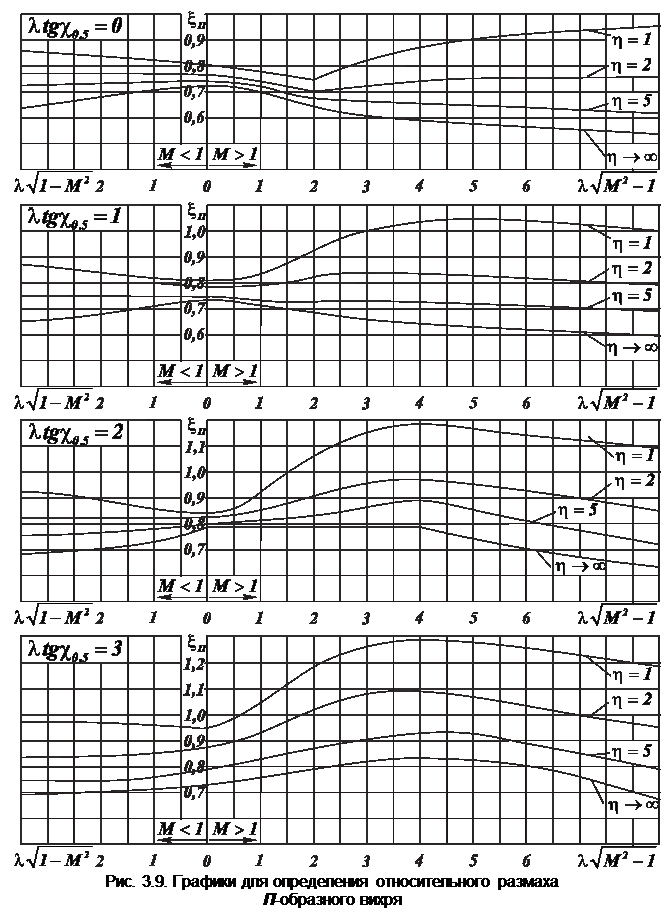
При больших значениях приведенного удлинения значения 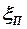стремятся к предельным значениям, определяемым формулой

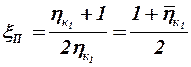. (3.49)

Пользуясь схемой П -образного вихря и некоторыми результатами обтекания оптимальных несущих систем, можно предложить следующую методику определения скоса потока в районе вторых несущих поверхностей.

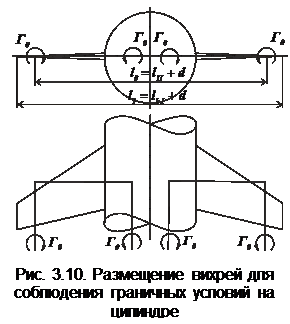Для соблюдения граничных условий на цилиндрическом корпусе схема П -образного вихря несколько преобразовывается и принимает вид, показанный на рис. 3.10. Например, при установке на корпус по схеме среднеплана консолей, изображённых на рис. 3.8, внутри корпуса необходимо разместить ещё два вихря в точках с координатами 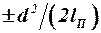(рис. 3.10). Отсюда для системы несущая поверхность-корпус имеем

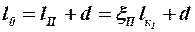. (3.50)

Эта вихревая структура, связанная с подъёмной силой впереди расположенных частей ЛА, создаёт в зоне вторых несущих поверхностей вертикальные скорости 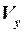, отклоняющие вектор скорости невозмущённого потока на угол скоса .

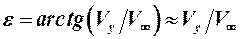Для вторых несущих поверхностей вводится осреднённый по размаху угол скоса 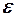. Если скос потока при 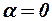равен нулю и зависимость 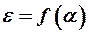можно считать линейной, то значение угла атаки вторых несущих поверхностей определяется следующим образом:

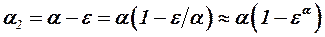. (3.51)

Величина производной 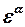по предлагаемой методике вычисляется по формуле

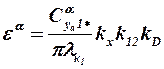. (3.52)

Здесь 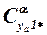– производная коэффициента подъёмной силы консолей первых несущих поверхностей, присоединённых к корпусу,

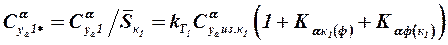, (3.53)

где 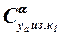– производная коэффициента подъёмной силы изолированных консолей первых несущих поверхностей.

Множитель 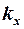учитывает положение вторых несущих поверхностей относительно первых и определяется по формулам

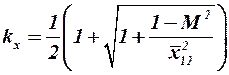при 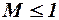, (3.54)

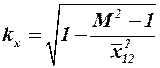при 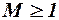, (3.55)

где 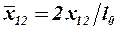, – расстояние между положениями центров давления (фокусами) первых и вторых изолированных несущих поверхностей, а 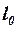вычисляется по (3.50).

В сверхзвуковом потоке при 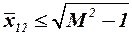необходимо полагать 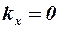и, следовательно, скос потока также будет равен нулю, т. е. 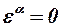. Это связано с тем обстоятельством, что при увеличении числа зона влияния свободных вихрей от первых несущих поверхностей, ограниченных конусом Маха, сужается и при определённых числах вторые несущие поверхности могут полностью выйти из этой зоны.

Параметр 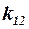зависит от геометрических характеристик второй несущей поверхности и её положения относительно свободных вихрей, сходящих с впереди расположенных частей ЛА. Если вторые несущие поверхности полностью находятся в зоне между свободными вихрями (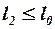), то 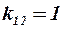. Если вторые несущие поверхности выходят из этой зоны (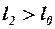), то это приводит к уменьшению осреднённого скоса потока. В этом случае коэффициент 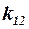определяется по формуле

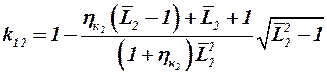, (3.56)

где .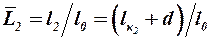

Коэффициент 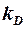в выражении (3.52) определяется по следующей формуле:

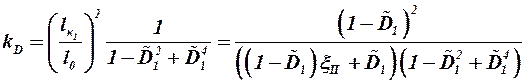. (3.57)

Множитель в этой формуле учитывает также дополнительное влияние корпуса на скос потока из-за воздействия отображённых внутрь корпуса вихрей (для соблюдения граничных условий).

Приведенные формулы позволяют определить по (3.7) и (3.8) величины производных от коэффициентов подъёмной силы и продольного момента ЛА по углу атаки при .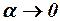

Глава 4

Дата добавления: 2014-12-26