Коэффициент волнового сопротивления летательного аппарата

2.5.1. Общие сведения о волновом сопротивлении

При скоростях полёта, соответствующих числам 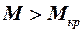, в потоке вблизи поверхности ЛА возникают скачки уплотнения, которые приводят к появлению волнового сопротивления и к резкому увеличению сопротивления ЛА и его частей.

Для уменьшения волнового сопротивления необходимо применять длинные корпусы с острыми носовыми частями. Относительная толщина профилей несущих поверхностей должна быть как можно меньше, так как волновое сопротивление пропорционально квадрату относительной толщины. Если большая часть траектории полёта ЛА происходит в диапазоне чисел , при котором передняя кромка несущей поверхности является сверхзвуковой, то для уменьшения волнового сопротивления необходимо применять профиль с заостренной передней кромкой. При дозвуковой передней кромке рекомендуется для реализации подсасывающей силы использовать профили с закруглённой передней кройкой. Для уменьшения волнового сопротивления в заданном диапазоне чисел необходимо соответствующим образом подбирать стреловидности несущих поверхностей или использовать «правило площадей».

Волновое сопротивление ЛА определяется суммой сопротивлений его частей с учетом их взаимного влияния. Однако для рассматриваемых ЛА обычно используются несущие поверхности с профилями малой относительной толщины (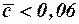), расположенные на цилиндрической части корпуса по схеме среднеплана, а «правило площадей» не используется. Поэтому расчётную формулу для коэффициента волнового сопротивления ЛА можно представить в следующем виде:

(2.43)

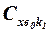где , и 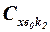– коэффициенты волнового сопротивления изолированных корпуса и несущих поверхностей; и 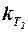– коэффициенты торможения потока в районе несущих поверхносте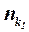й; и – количество консолей несущих поверхностей. Числовой коэффициент учитывает возможное увеличение коэффициента волнового сопротивления за счет неучтённых элементов (стыки обшивок, сварочные швы, заклёпки и т. п.).

2.5.2. Коэффициент волнового сопротивления
корпуса

Поскольку волновое сопротивление обусловлено нормальными составляющими поверхностных сил, то оно создаётся только теми элементами конструкции, которые имеют отличные от нуля углы наклона образующей. Поэтому волновое сопротивление корпуса при 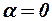определяется сопротивлениями носовой и кормовой частей. Цилиндрическая часть оказывает влияние только на формирование потока у кормы, а следовательно, и на величину её сопротивления. Однако при можно принять, что поток при подходе к кормовой части корпуса имеет фактически параметры невозмущённого потока, поэтому влиянием цилиндрической части на волновое сопротивление кормы можно пренебречь.

Итак, для расчета коэффициента волнового сопротивления корпуса имеем следующую формулу:

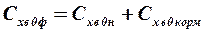,(2.44)

где и – коэффициенты волнового сопротивления носовой и кормовой частей корпуса.

На рис. 2.7 представлены графики изменения коэффициента в зависимости от числа конических и оживальных носовых частей.

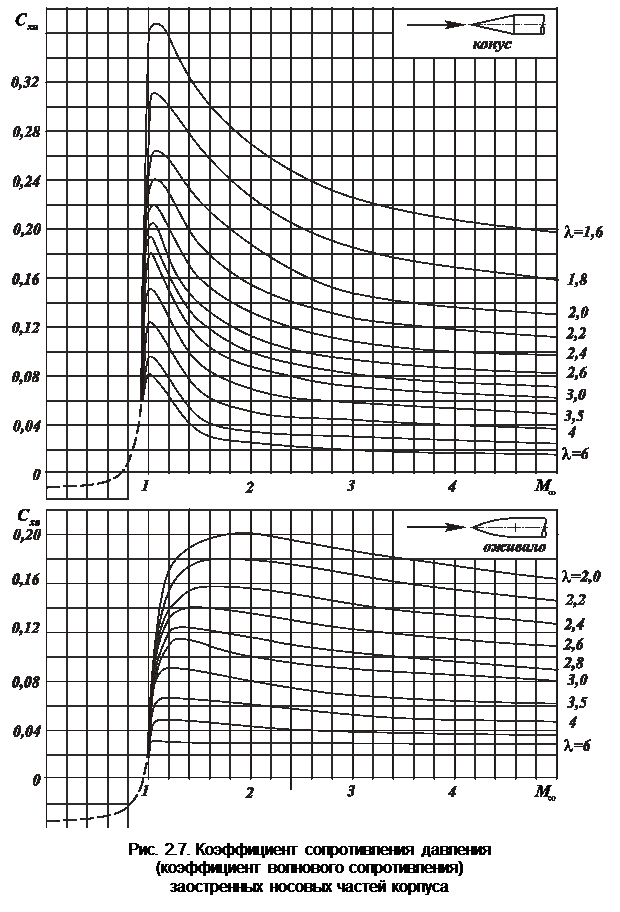
На графиках также приведены значения коэффициента сопротивления давления и при дозвуковых скоростях. При таком обтекании на некоторых участках носовой части возникает пониженное давление, вследствие чего может появиться подсасывающая сила (). Для обычных носовых частей её величина очень мала, поэтому при 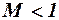можно принимать .

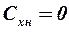Однако при использовании затупленных носовых частей малого удлинения (рис. 2.8) их сопротивление давления должно быть учтено и в дозвуковом диапазоне чисел . На этом рисунке пунктиром показаны значения максимального коэффициента сопротивления некоторых носовых частей. Максимальное сопротивление имеет носовая часть, выполненная в форме плоского торца.

Для определения коэффициента волнового сопротивления сужающейся конической кормовой части можно рекомендовать формулу

, (2.45)

а для конической расширяющейся –

, (2.46)

где значение коэффициента для фиктивного удлинения кормовой части

(2.47)

определяется по графикам на рис. 2.7.

Для кормовой части с криволинейной образующей

.(2.48)

Формулы для определения волнового сопротивления кормовых частей построены без учета влияния пограничного слоя. На кормовой части корпуса обычно имеется довольно толстый пограничный слой, что может сильно уменьшить величину коэффициента .

2.5.3. Коэффициент волнового сопротивления
несущих поверхностей

Волновое сопротивление несущих поверхностей, как и других частей летательного аппарата, возникает при 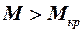. Однако систематические исследования имеются только при сверхзвуковых скоростях полёта, т. е. при 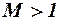. При необходимости волновое сопротивление несущих поверхностей в трансзвуковом диапазоне чисел можно определить по следующей приближенной формуле [13]:

. (2.49)

Здесь 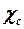– угол стреловидности по линии максимальных толщин; 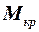– критическое число ; – число , соответствующее максимальному значению коэффициента волнового сопротивления при околозвуковых скоростях,

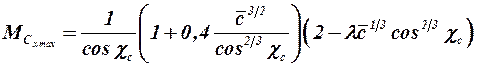. (2.50)

При сверхзвуковых скоростях полёта коэффициент волнового сопротивления несущей поверхности согласно линеаризованной теории зависит от числа , формы поверхности в плане, а также от относительной толщины и формы профиля. Форма трапециевидной поверхности характеризуется удлинением , сужением 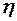и стреловидностью по любой линии -частей хорд. Число независимых переменных можно значительно уменьшить, введя обобщённые параметры. В этом случае можно записать

.

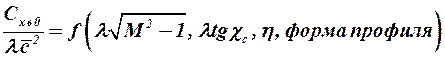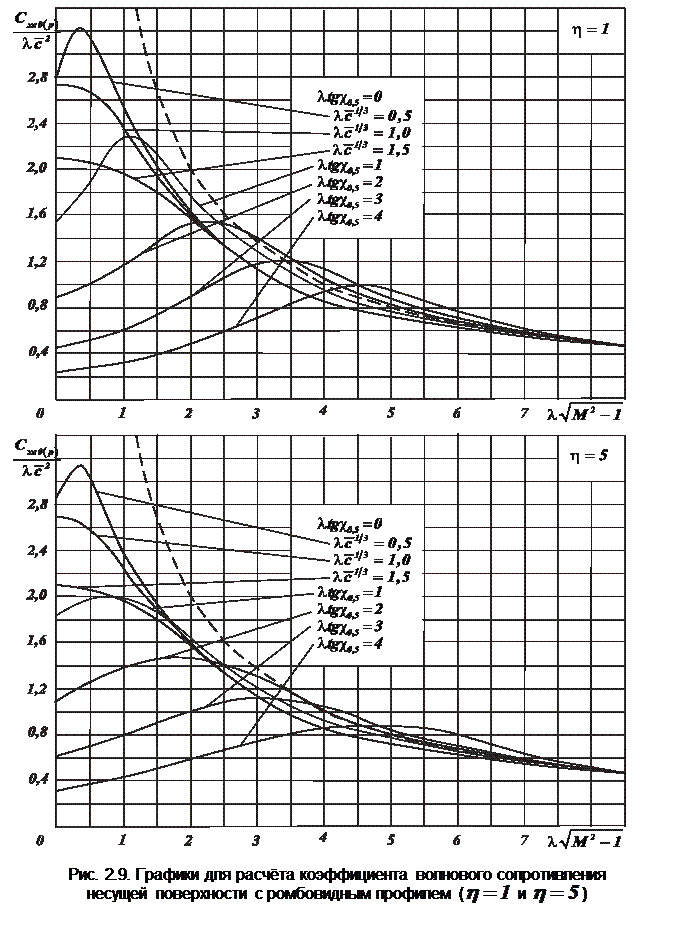
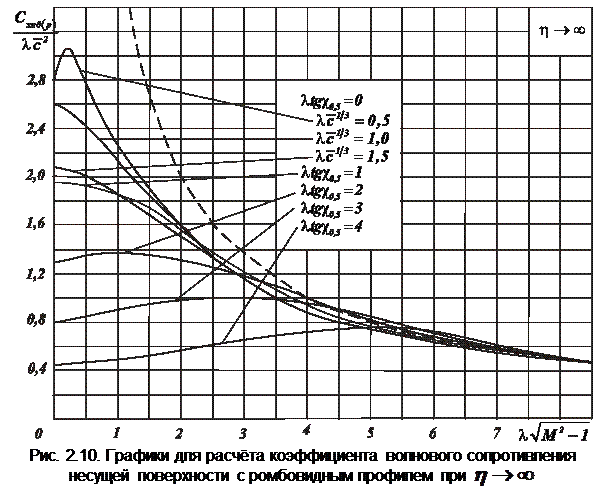
На рис. 2.9 и 2.10 представлены графики этих значений для трапециевидных крыльев с ромбовидным профилем [8]. Они соответствуют определённым значениям сужения: 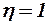, и 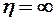. При увеличении числа , или, точнее, приведенного удлинения 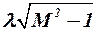, влияние формы несущей поверхности уменьшается. Это можно объяснить сужением конусов Маха (при увеличении числа ), выходящих из точек излома передней кромки и из передних точек боковых кромок.

Поэтому при больших значениях приведенного удлинения (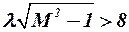) коэффициент волнового сопротивления поверхности с ромбовидным профилем может быть определён по формуле

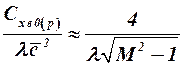, (2.51)

как для профиля (крыла бесконечного размаха).

Следует отметить, что экспериментальные значения коэффициента волнового сопротивления заметно расходятся с теоретическими особенно в областях, где теоретические кривые имеют резко выраженные пики. Здесь для определения волнового сопротивления линейная теория неприменима. Максимального значения коэффициент волнового сопротивления достигает тогда, когда линия максимальных толщин переходит с дозвукового обтекания к сверхзвуковому (по линейной теории). Однако если при 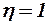это происходит действительно при , то при увеличении сужения этот максимум смещается к меньшим значениям приведенного удлинения,
т. е. при 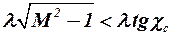. В этом случае смещение тем больше, чем больше сужение поверхности.

При больших значениях приведенного удлинения 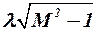, когда линия максимальных толщин становится существенно сверхзвуковой, т е. при , схожесть теоретических значений с экспериментальными значительно лучше, но всё же и здесь теоретические значения волнового сопротивления несколько завышены. Это можно объяснить тем, что поток за точкой максимальной толщины расширяется не полностью из-за наличия пограничного слоя, что приводит к повышению давления в этой области, а следовательно, и к уменьшению волнового сопротивления. Так, например, исследование ромбовидных профилей в аэродинамической трубе показывают, что экспериментальные данные меньше теоретических приблизительно на 13%.

Следует иметь в виду, что при малых сверхзвуковых скоростях полёта коэффициент волнового сопротивления также зависит от параметра трансзвукового подобия . Однако приведенные данные позволяют учесть это влияние только для 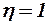. Для приближенного определения коэффициента волнового сопротивления в этом диапазоне чисел полёта можно воспользоваться формулой (2.49).

Графики, полученные для поверхностей с ромбовидным профилем, могут быть использованы для определения волнового сопротивления поверхности с произвольным профилем.(имеются в виду профили с конфигурацией, характерной для скоростных манёвренных ЛА).

Влияние формы профиля на волновое сопротивление профилей (прямых крыльев бесконечного размаха) в настоящее время хорошо изучено теоретически и экспериментально. Очень эффективным оказалось введение коэффициента 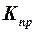, представляющего отношение коэффициента волнового сопротивления данного профиля к аналогичному коэффициенту ромбовидного профиля , т. е. .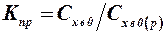

Влияние формы профиля на волновое сопротивление крыльев конечного размаха оказывается несколько иным. Анализ экспериментальных данных показывает, что при , т. е. когда линия максимальных толщин дозвуковая, форма профиля незначительно влияет на волновое сопротивление. При существенно сверхзвуковой линии максимальных толщин (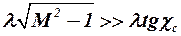) влияние формы профиля на коэффициент примерно такое же, как и для профиля. Если эта линия сверхзвуковая (т. е. при ), то, следуя методике, изложенной в работе [8], коэффициент волнового сопротивления несущей поверхности с произвольным профилем можно представить в следующем виде:

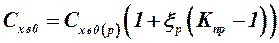, (2.52)

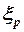где множитель находится с помощью графика на рис. 2.11, коэффициент – с помощью графиков на рис. 2.9 (в зависимости от параметров поверхности), коэффициент 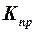определяется по таблице, приведенной в прил. 2. Это позволяет воспользоваться приведенными графиками для широкого класса профилей.

Значение множителя 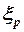можно также приближенно определить по следующей формуле [8]:

. (2.53)

При увеличении значений разности 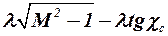влияние формы профиля на коэффициент волнового сопротивления возрастает. При существенно сверхзвуковой линии максимальных толщин (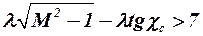) влияние формы профиля на коэффициент волнового сопротивления несущей поверхности примерно такое же, как и для профиля (прямоугольного крыла бесконечного размаха).

Необходимо иметь в виду, что при вычислении коэффициентов волнового сопротивления несущих поверхностей в формулы должны быть подставлены геометрические параметры соответствующих поверхностей и числа с учётом коэффициента торможения потока ().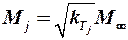

Глава 3

Дата добавления: 2014-12-26