
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент сопротивления трения летательного аппарата
|
|
|
|
2.2.1. Общие сведения о сопротивлении трения
Сопротивление трения ЛА определяется суммой трения отдельных его частей с учётом их взаимного влияния. Формула для определения коэффициента сопротивления трения имеет вид
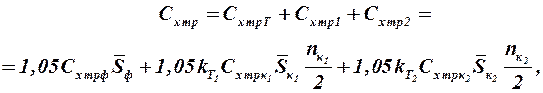 (2.5)
(2.5)
где 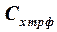 ,
,  и
и 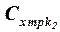 – коэффициенты сопротивления изолированных корпуса (фюзеляжа) и несущих поверхностей.
– коэффициенты сопротивления изолированных корпуса (фюзеляжа) и несущих поверхностей.
При расчете коэффициентов сопротивления трения изолированных частей используется методика ЦАГИ, согласно которой сопротивление трения любого удобообтекаемого тела (например, несущей поверхности) определяется через сопротивление трения плоской пластинки. Согласно этой методике,
 . (2.6)
. (2.6)
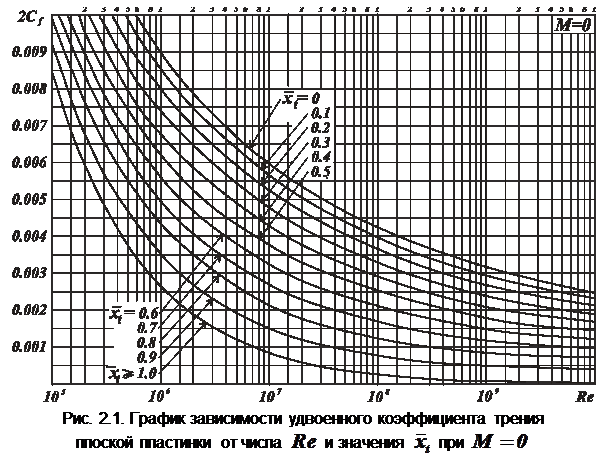 Здесь
Здесь  – коэффициент сопротивления трения одной стороны плоской пластинки в несжимаемом потоке (
– коэффициент сопротивления трения одной стороны плоской пластинки в несжимаемом потоке (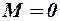 ) при одинаковых с данным телом числе Рейнольдса
) при одинаковых с данным телом числе Рейнольдса 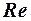 и положении точки перехода ламинарного пограничного слоя в турбулентный
и положении точки перехода ламинарного пограничного слоя в турбулентный 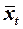 . Удвоенное значение коэффициента
. Удвоенное значение коэффициента  учитывает обтекание пластинки с двух сторон. График зависимости
учитывает обтекание пластинки с двух сторон. График зависимости 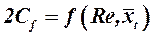 приведен на рис. 2.1.
приведен на рис. 2.1.
Коэффициент  учитывает влияние сжимаемости (числа
учитывает влияние сжимаемости (числа  ) на сопротивление трения плоской пластинки, а коэффициент
) на сопротивление трения плоской пластинки, а коэффициент  – влияние градиента давления (формы тела) на сопротивление трения.
– влияние градиента давления (формы тела) на сопротивление трения.
Приведенные данные соответствуют гладким поверхностям. Реальные ЛА всегда имеют шероховатую поверхность, зависящую от технологии процесса её обработки. Шероховатость поверхности турбулизирует пограничный слой, т. е. смещает точку перехода к носику тела. Однако по мере роста числа  это влияние становится менее заметным. Поэтому при увеличении числа
это влияние становится менее заметным. Поэтому при увеличении числа  требования к чистоте поверхности могут быть значительно снижены практически без ущерба для аэродинамических характеристик ЛА. Здесь речь идёт об увеличении шероховатости в разумных пределах.
требования к чистоте поверхности могут быть значительно снижены практически без ущерба для аэродинамических характеристик ЛА. Здесь речь идёт об увеличении шероховатости в разумных пределах.
Число 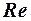 рассчитывается по параметрам потока перед обтекаемым телом и характерному размеру этого тела
рассчитывается по параметрам потока перед обтекаемым телом и характерному размеру этого тела 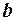 :
:
 , (2.7)
, (2.7)
где функция 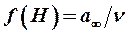 (
( – скорость звука,
– скорость звука,  – кинематический коэффициент вязкости) определяется для заданной высоты полёта
– кинематический коэффициент вязкости) определяется для заданной высоты полёта 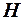 через параметры стандартной атмосферы. Значения
через параметры стандартной атмосферы. Значения  (её размерность м-1) для ряда высот приведены в табл. 2.1.
(её размерность м-1) для ряда высот приведены в табл. 2.1.
Таблица 2.1
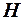 , , 
| |||||||||||
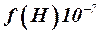
| 2,330 | 1,939 | 1,601 | 1,310 | 1,061 | 0,850 | 0,647 | 0,473 | 0,345 | 0,252 | 0,184 |
Значения функции  при
при  удовлетворительно аппроксимирует следующая формула:
удовлетворительно аппроксимирует следующая формула:
 , (2.8)
, (2.8)
где 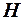 – высота полёте,
– высота полёте,  .
.
Влияние числа  на коэффициент трения показано на рис. 2.2.
на коэффициент трения показано на рис. 2.2.
Определение точного положения точки перехода 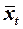 ламинарного пограничного слоя в турбулентный даже для изолированных частей ЛА довольно затруднительно. Это объясняется частично тем, что на положение точки перехода оказывают влияние многие факторы (числа
ламинарного пограничного слоя в турбулентный даже для изолированных частей ЛА довольно затруднительно. Это объясняется частично тем, что на положение точки перехода оказывают влияние многие факторы (числа 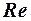 и
и  , чистота поверхности, градиент давления вдоль тела, явления теплообмена и т. п.), систематические исследования по которым пока отсутствуют. Кроме того, положения точек перехода, определённые для изолированных частей, могут сильно измениться при установке этих частей на ЛА, т. е. положение зон перехода также сильно зависит от компоновки ЛА и режима полёта.
, чистота поверхности, градиент давления вдоль тела, явления теплообмена и т. п.), систематические исследования по которым пока отсутствуют. Кроме того, положения точек перехода, определённые для изолированных частей, могут сильно измениться при установке этих частей на ЛА, т. е. положение зон перехода также сильно зависит от компоновки ЛА и режима полёта.
Например, при сверхзвуковой скорости полёта и малом угле атаки из мест стыка передних кромок несущих поверхностей с корпусом выходит скачок уплотнения, «соприкасающийся» с поверхностью корпуса по двум линиям. Резкое увеличение давления за скачком уплотнения стремится вызвать переход ламинарного пограничного слоя в турбулентный вдоль этих линий. При увеличении угла атаки давление на верхней поверхности снижается и этот переход может не произойти. Следует отметить, что положение зоны перехода зависит также от характера движения, наличия тряски и других причин и может быть определено только на основании экспериментальных данных.
При аэродинамическом расчёте на начальном этапе проектирования допустимо считать, что на всех элементах конструкции ЛА формируется турбулентный пограничный слой (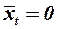 ). В этом случае величина сопротивления трения ЛА получается несколько завышенной, что создаёт некоторый «гарантийный запас» в получении требуемых лётных характеристик.
). В этом случае величина сопротивления трения ЛА получается несколько завышенной, что создаёт некоторый «гарантийный запас» в получении требуемых лётных характеристик.
Для расчёта коэффициента сопротивления трения при турбулентном пограничном слое (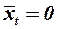 ) можно воспользоваться следующими формулами:
) можно воспользоваться следующими формулами:
 при
при  ; (2.9)
; (2.9)
 при
при 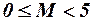 . (2.10)
. (2.10)
Для определения этих величин при известном положении зоны перехода необходимо пользоваться графиками, приведенными на рис. 2.1 и 2.2.
Следует заметить, что представленные формулы и графики справедливы только при отсутствии теплообмена между средой и телом. При наличии теплопередачи можно использовать приближенный метод расчета сопротивления трения, представленный в работе [7].
2.2.2. Коэффициент сопротивления трения
корпуса
Для приближенного определения коэффициента сопротивления трения корпуса можно использовать рассмотренный выше метод, если большая часть корпуса является цилиндрической и отношение толщины вытеснения пограничного слоя к радиусу цилиндра не превышает  . В этом случае
. В этом случае
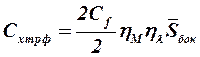 . (2.11)
. (2.11)
Здесь 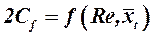 определяется по графикам на рис. 2.1, а коэффициент
определяется по графикам на рис. 2.1, а коэффициент 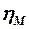 , учитывающий влияние числа
, учитывающий влияние числа  , – по графику на рис. 2.2; величина отношения площади боковой («смоченной») поверхности к площади миделя приближённо определяется по (1.12). Коэффициент
, – по графику на рис. 2.2; величина отношения площади боковой («смоченной») поверхности к площади миделя приближённо определяется по (1.12). Коэффициент  зависит от геометрии корпуса и может быть приближённо определён через его удлинение:
зависит от геометрии корпуса и может быть приближённо определён через его удлинение:
 . (2.12)
. (2.12)
Число 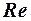 корпуса вычисляется по его длине
корпуса вычисляется по его длине 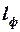 и параметрам полёта
и параметрам полёта  и
и 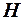 :
:
 . (2.13)
. (2.13)
При наличии на корпусе полностью турбулентного пограничного слоя (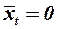 ) для определения коэффициентов
) для определения коэффициентов  и
и 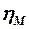 можно использовать формулы (2.9) и (2.10).
можно использовать формулы (2.9) и (2.10).
Отсюда коэффициент трения корпуса, отнесённый к характерной площади ЛА, определяется по формуле
 . (2.14)
. (2.14)
2.2.3. Коэффициент торможения потока
в районе первых несущих поверхностей
При дозвуковых скоростях полёта передние несущие поверхности обтекаются практически невозмущённым потоком. Однако при полёте со сверхзвуковыми скоростями перед носовой частью корпуса возникает скачок уплотнения, что приводит к потере полного давления и уменьшению скорости потока перед несущей поверхностью. По размаху консоли эти величины будут изменяться, поэтому удобно их усреднить по размаху. Степень торможения потока можно охарактеризовать средним коэффициентом торможения  , для которого скоростной напор
, для которого скоростной напор  находят по некоторой осредненной величине числа
находят по некоторой осредненной величине числа  возмущённого потока перед несущей поверхностью (
возмущённого потока перед несущей поверхностью (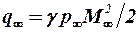 – скоростной напор невозмущённого потока). Полагая давление в возмущённом и невозмущённом потоках одинаковыми (
– скоростной напор невозмущённого потока). Полагая давление в возмущённом и невозмущённом потоках одинаковыми ( ), осреднённый коэффициент торможения можно выразить отношением
), осреднённый коэффициент торможения можно выразить отношением  . Этот коэффициент для первых несущих поверхностей при дозвуковых скоростях полёта незначительно отличается от единицы, а при сверхзвуковых скоростях его величина зависит от характера и интенсивности скачка уплотнения, возникающего перед головной частью ЛА. К сожалению, по данному вопросу систематические исследования пока отсутствуют.
. Этот коэффициент для первых несущих поверхностей при дозвуковых скоростях полёта незначительно отличается от единицы, а при сверхзвуковых скоростях его величина зависит от характера и интенсивности скачка уплотнения, возникающего перед головной частью ЛА. К сожалению, по данному вопросу систематические исследования пока отсутствуют.
 При выполнении предварительных расчётов для первых несущих поверхностей можно при дозвуковых скоростях полёта принимать
При выполнении предварительных расчётов для первых несущих поверхностей можно при дозвуковых скоростях полёта принимать 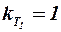 , а при сверхзвуковых скоростях использовать график рис. 2.3, построенный по материалам теоретических расчетов, приведенным в работе [8]. На этом графике изображена зависимость коэффициента торможения потока
, а при сверхзвуковых скоростях использовать график рис. 2.3, построенный по материалам теоретических расчетов, приведенным в работе [8]. На этом графике изображена зависимость коэффициента торможения потока  от числа
от числа  для различных значений коэффициента волнового сопротивления головной части корпуса (см. подразд. 2.5.2). Если коэффициент волнового сопротивления головной части и число
для различных значений коэффициента волнового сопротивления головной части корпуса (см. подразд. 2.5.2). Если коэффициент волнового сопротивления головной части и число  не очень велики, то в первом приближении можно и при сверхзвуковых скоростях полёта принимать
не очень велики, то в первом приближении можно и при сверхзвуковых скоростях полёта принимать 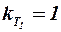 .
.
2.2.4. Коэффициент сопротивления трения
первых несущих поверхностей
Коэффициент сопротивления трения передних несущих поверхностей по рассмотренной ранее методике определяется по формуле
 , (2.15)
, (2.15)
 где
где 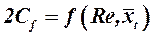 определяется по графику рис. 2.1, коэффициент
определяется по графику рис. 2.1, коэффициент 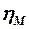 , учитывающий влияние числа
, учитывающий влияние числа  , – по графику рис. 2.2, а коэффициент
, – по графику рис. 2.2, а коэффициент 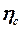 , частично учитывающий изменение градиента давления по профилю, определяется по относительной толщине профиля и положению точки перехода ламинарного пограничного слоя в турбулентный по графику
, частично учитывающий изменение градиента давления по профилю, определяется по относительной толщине профиля и положению точки перехода ламинарного пограничного слоя в турбулентный по графику
рис. 2.4.
Число 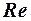 определяется по параметрам потока в области передних несущих поверхностей и по средней хорде её консоли
определяется по параметрам потока в области передних несущих поверхностей и по средней хорде её консоли 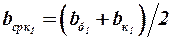 :
:
 . (2.16)
. (2.16)
При обтекании поверхности турбулентным пограничным слоем (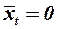 ) для определения коэффициентов
) для определения коэффициентов  и
и 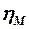 можно использовать формулы (2.9) и (2.10), а величину коэффициента
можно использовать формулы (2.9) и (2.10), а величину коэффициента 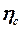 при
при  вычислять по следующей формуле:
вычислять по следующей формуле:
 , (2.17)
, (2.17)
где  – относительная толщина профиля передних несущих поверхностей.
– относительная толщина профиля передних несущих поверхностей.
Отсюда коэффициент трения передних консолей, отнесённый к характерной площади ЛА:
 . (2.18)
. (2.18)
2.2.5. Коэффициент торможения потока
в районе вторых несущих поверхностей
Вторые несущие поверхности полностью или частично находятся в заторможенном потоке от корпуса и впереди расположенных несущих поверхностей. Коэффициент торможения потока в этом районе удобно представить в виде произведения коэффициента торможения от головной части корпуса  и коэффициента торможения от впереди расположенных несущих поверхностей
и коэффициента торможения от впереди расположенных несущих поверхностей 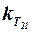 :
:
 , (2.19)
, (2.19)
где  определяется согласно подразд. 2.2.3.
определяется согласно подразд. 2.2.3.
Коэффициент торможения потока 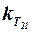 зависит от взаимного расположения консолей первых и вторых несущих поверхностей, числа
зависит от взаимного расположения консолей первых и вторых несущих поверхностей, числа  и сопротивления впереди расположенных несущих поверхностей. При этом если консоли первых и вторых несущих поверхностей находятся в разных плоскостях, то при малых углах атаки торможением потока от впереди расположенных поверхностей можно пренебречь, т. е. принять
и сопротивления впереди расположенных несущих поверхностей. При этом если консоли первых и вторых несущих поверхностей находятся в разных плоскостях, то при малых углах атаки торможением потока от впереди расположенных поверхностей можно пренебречь, т. е. принять 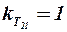 . Если консоли первых и вторых несущих поверхностей находятся в одной плоскости, но размах вторых несущих поверхностей больше размаха впереди расположенных (
. Если консоли первых и вторых несущих поверхностей находятся в одной плоскости, но размах вторых несущих поверхностей больше размаха впереди расположенных (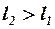 ), то часть вторых несущих поверхностей уже не будет попадать в аэродинамический след от впереди расположенных поверхностей. В этом случае для определения осреднённого коэффициента торможения потока
), то часть вторых несущих поверхностей уже не будет попадать в аэродинамический след от впереди расположенных поверхностей. В этом случае для определения осреднённого коэффициента торможения потока 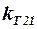 можно рекомендовать приближённую формулу:
можно рекомендовать приближённую формулу:
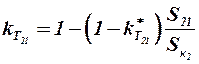 , (2.20)
, (2.20)
где 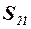 – площадь консолей вторых несущих поверхностей, попадающая в аэродинамический след от впереди расположенных поверхностей;
– площадь консолей вторых несущих поверхностей, попадающая в аэродинамический след от впереди расположенных поверхностей;  – коэффициент торможения потока за впереди расположенной несущей поверхностью в районе вторых поверхностей.
– коэффициент торможения потока за впереди расположенной несущей поверхностью в районе вторых поверхностей.
Если вторые несущие поверхности полностью находятся в аэродинамическом следе за первыми (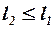 , т. е.
, т. е. 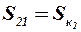 ), то
), то
 . (2.21)
. (2.21)
Коэффициент торможения потока  при дозвуковых скоростях полёта можно вычислять по формуле
при дозвуковых скоростях полёта можно вычислять по формуле
 . (2.22)
. (2.22)
 Здесь
Здесь  – коэффициент сопротивления консолей первых несущих поверхностей, определяемый по формуле (2.15);
– коэффициент сопротивления консолей первых несущих поверхностей, определяемый по формуле (2.15);  , где
, где  – расстояние от задней кромки впереди расположенной поверхности до передней кромки второй поверхности (рис. 2.5) в плоскости, проходящей через середину консоли второй поверхности (при
– расстояние от задней кромки впереди расположенной поверхности до передней кромки второй поверхности (рис. 2.5) в плоскости, проходящей через середину консоли второй поверхности (при 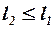 ) или через середину консоли передней поверхности (при
) или через середину консоли передней поверхности (при 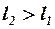 );
); 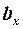 – хорда консоли впереди расположенной поверхности в этом сечении.
– хорда консоли впереди расположенной поверхности в этом сечении.
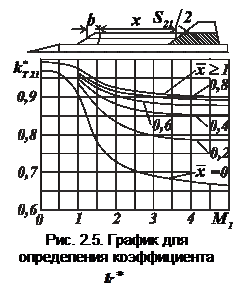
При сверхзвуковых скоростях полёта величину коэффициента 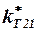 можно приближённо определить по графику рис. 2.5, полученному в результате обработки экспериментальных данных [8].
можно приближённо определить по графику рис. 2.5, полученному в результате обработки экспериментальных данных [8].
Приведенные формулы и графики позволяют определить коэффициент торможения потока в районе вторых несущих поверхностей.
2.2.6. Коэффициент сопротивления трения
вторых несущих поверхностей
Расчёт коэффициента сопротивления трения вторых несущих поверхностей выполняется по тем же формулам и графикам, что и для первых (см. подразд. 2.2.4), только при вычислениях используются параметры, соответствующие вторым несущим поверхностям, и учитывается, что число  в этом случае равно
в этом случае равно  .
.
Коэффициент сопротивления трения по рассмотренной ранее методике определяется по формуле
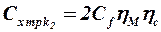 , (2.23)
, (2.23)
где 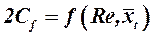 находится по графику рис. 2.1, коэффициент
находится по графику рис. 2.1, коэффициент 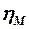 , учитывающий влияние числа
, учитывающий влияние числа  , – по графику рис. 2.2, а коэффициент
, – по графику рис. 2.2, а коэффициент 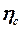 , частично учитывающий форму профиля, – по графику рис. 2.4. Число
, частично учитывающий форму профиля, – по графику рис. 2.4. Число 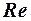 вычисляется по параметрам потока в области вторых несущих поверхностей и по средней хорде их консолей
вычисляется по параметрам потока в области вторых несущих поверхностей и по средней хорде их консолей  :
:
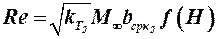 . (2.24)
. (2.24)
При обтекании поверхности турбулентным пограничным слоем (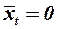 ) для определения коэффициентов
) для определения коэффициентов  и
и 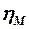 можно использовать формулы (2.9) и (2.10), а величину коэффициента
можно использовать формулы (2.9) и (2.10), а величину коэффициента 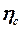 при
при  вычислять по формуле (2.17), где
вычислять по формуле (2.17), где  – относительная толщина профиля вторых несущих поверхностей.
– относительная толщина профиля вторых несущих поверхностей.
Отсюда коэффициент трения вторых консолей, отнесённый к характерной площади ЛА:
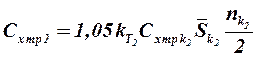 . (2.25)
. (2.25)
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 2346; Нарушение авторских прав?; Мы поможем в написании вашей работы!