
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент подъемной силы и продольного момента летательного аппарата при . Центр давления и фокус по углу атаки летательного аппарата
|
|
|
|
ЛЕТАТЕЛЬНОГО АППАРАТА И ЕГО ЧАСТЕЙ
И ПОЛОЖЕНИЕ ФОКУСА ПО УГЛУ АТАКИ
ПОДЪЁМНОЙ СИЛЫ ПО УГЛУ АТАКИ
ПРОИЗВОДНАЯ ОТ КОЭФФИЦИЕНТА
ПРИ 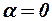 И
И 
Рассматриваемые ЛА компонуются из корпуса большого удлинения и несущих поверхностей обычно малого удлинения. Для них характерно нелинейное изменение подъёмной силы и продольного момента по углам атаки. Поэтому аналогичными свойствами обладают и аэродинамические коэффициенты ЛА. Для ЛА, обладающего горизонтальной плоскостью симметрии, формулы для изменение коэффициентов подъёмной силы и продольного момента по углам атаки удобно представить в виде суммы двух слагаемых. Первые слагаемые (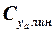 и
и  ) изменяются по линейному закону от угла атаки, а вторые (
) изменяются по линейному закону от угла атаки, а вторые (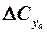 и
и  ) – по почти квадратичному:
) – по почти квадратичному:
 ; (3.1)
; (3.1)
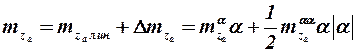 . (3.2)
. (3.2)
Здесь  и
и  – производные от коэффициентов подъёмной силы и продольного момента по углу атаки при
– производные от коэффициентов подъёмной силы и продольного момента по углу атаки при 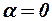 ; коэффициенты
; коэффициенты  и
и  – вторые производные по углу атаки при
– вторые производные по углу атаки при 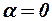 .
.
При проектировании и «эксплуатации» ЛА удобно иметь моментные характеристики, определяемые относительно различных точек. Разработанные и используемые на кафедре аэродинамики программы расчёта аэродинамических характеристик ЛА позволяют задавать любую точку отсчёта моментных характеристик, а также характерные для ЛА длину и площадь. При аэродинамических расчётах удобно в качестве такой точки приведения выбрать фиксированную точку, связанную с телом. Для удобства изложения далее продольный момент ЛА будет определяться относительно носика корпуса, а в качестве характерной длины для него выбрана длина корпуса.
При рассмотрении задач динамики полёта используется система координат, начало которой расположено в центре масс ЛА. В качестве характерной длины иногда удобнее использовать другой линейный размер. Пересчёт значений коэффициента продольного момента от одной оси приведения к другой, а также к иному характерному размеру выполняется очень просто. Например, коэффициент продольного момента  , измеряемый от центра масс ЛА и отнесённый к характерному размеру
, измеряемый от центра масс ЛА и отнесённый к характерному размеру  , определяется через
, определяется через  по следующей справедливой только при малых углах атаки формуле:
по следующей справедливой только при малых углах атаки формуле:
 . (3.3)
. (3.3)
Здесь 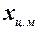 – расстояние от носика корпуса до центра масс ЛА;
– расстояние от носика корпуса до центра масс ЛА; 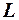 и
и  – прежний и новый характерные размеры. В данных условиях предполагается, что продольный момент рассматривается только от подъёмной силы, хотя следует учитывать момент и от лобового сопротивления.
– прежний и новый характерные размеры. В данных условиях предполагается, что продольный момент рассматривается только от подъёмной силы, хотя следует учитывать момент и от лобового сопротивления.
При вычислении продольного момента удобно работать с проекциями аэродинамической силы в связанной системе. В этом случае формула (3.3), но уже справедливая при любых углах атаки, для ЛА, имеющего горизонтальную плоскость симметрии, приобретает вид
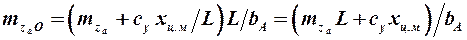 .
.
Для решения задач, связанных с балансировкой, устойчивостью и управляемостью, необходимо знать положение центра давления и фокуса ЛА. Центром давления принято считать точку пересечения результирующей аэродинамической силы с продольной осью ЛА. Фокусом по какому-либо параметру называется точка пересечения линии приращения аэродинамической силы с осью ЛА при малом изменении этого параметра (например, угла атаки, угла поворота управляющей поверхности, высоты полёта и т. п.). Здесь будет рассматриваться только фокус по углу атаки. Вместо этого термина далее будет употребляться для краткости термин «фокус». Сказанное выше относится также к отдельным частям ЛА и их комбинациям.
Положения центра давления 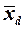 и фокуса по углу атаки
и фокуса по углу атаки 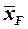 определяются по следующим формулам:
определяются по следующим формулам:
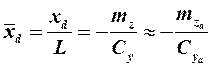 ; (3.4)
; (3.4)
 , (3.5)
, (3.5)
где 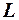 – характерный размер.
– характерный размер.
Как и другие аэродинамические характеристики, подъёмная сила ЛА определяется суммой подъёмных сил его изолированных частей, а также дополнительных слагаемых, учитывающих взаимное влияние между ними. Например, 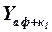 – подъёмная сила корпуса и установленных на нём первых несущих поверхностей удобно представить следующим образом:
– подъёмная сила корпуса и установленных на нём первых несущих поверхностей удобно представить следующим образом:
 , (3.6)
, (3.6)
где 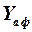 и
и 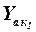 – подъёмные силы изолированных корпуса и консолей первых несущих поверхностей, а последние два слагаемых являются дополнительными силами, возникающими из-за влияния корпуса на подъёмную силу консолей (
– подъёмные силы изолированных корпуса и консолей первых несущих поверхностей, а последние два слагаемых являются дополнительными силами, возникающими из-за влияния корпуса на подъёмную силу консолей ( ) и влияния консолей на подъёмную силу корпуса (
) и влияния консолей на подъёмную силу корпуса ( ). Аналогичным образом можно записать выражение и для продольного момента этой комбинации. Эти вопросы интерференции между частями ЛА будут рассмотрены ниже.
). Аналогичным образом можно записать выражение и для продольного момента этой комбинации. Эти вопросы интерференции между частями ЛА будут рассмотрены ниже.
В данной главе будут рассмотрены коэффициенты подъёмной силы и продольного момента ЛА и его отдельных частей при 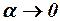 и неотклонённых рулевых поверхностях. Эти характеристики определяются производными от коэффициентов по углу атаки при
и неотклонённых рулевых поверхностях. Эти характеристики определяются производными от коэффициентов по углу атаки при 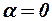 .
.
Величины производных от коэффициентов подъёмной силы и продольного момента ЛА по углу атаки при 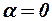 удобно записать так:
удобно записать так:
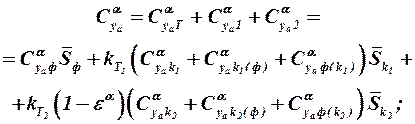 (3.7)
(3.7)
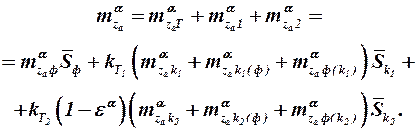 (3.8)
(3.8)
Здесь  и
и 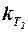 – коэффициенты торможения потока в районе несущих поверхностей, множитель (
– коэффициенты торможения потока в районе несущих поверхностей, множитель (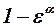 ) учитывает то обстоятельство, что вторые несущие поверхности обтекаются потоком, скошенным вихревой пеленой, сходящей с впереди расположенных частей ЛА; подстрочные индексы введены по аналогии с формулой (3.6).
) учитывает то обстоятельство, что вторые несущие поверхности обтекаются потоком, скошенным вихревой пеленой, сходящей с впереди расположенных частей ЛА; подстрочные индексы введены по аналогии с формулой (3.6).
Для ЛА, имеющего горизонтальную плоскость симметрии, при 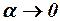 центр давления
центр давления 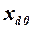 будет совпадать с фокусом
будет совпадать с фокусом  . Их положение определяется по формуле
. Их положение определяется по формуле
 . (3.9)
. (3.9)
Перейдём к определению величин, входящих в приведенные выше формулы.
1.6. Производные от коэффициентов подъёмной силы
и продольного момента корпуса по углу атаки при 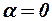
Формулы для подъёмной силы и продольного момента корпуса удобно представить суммой, содержащей слагаемые, отражающие роль носовой, цилиндрической и кормовой частей. Для их производных имеем
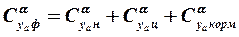 , (3.10)
, (3.10)
 (3.11)
(3.11)
где 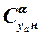 ,
, 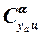 и
и  – производные от коэффициентов подъёмных сил носовой, цилиндрической и кормовой частей корпуса по углу атаки;
– производные от коэффициентов подъёмных сил носовой, цилиндрической и кормовой частей корпуса по углу атаки;  ,
,  и
и  – положения фокусов этих частей.
– положения фокусов этих частей.
По теории тонкого тела [3] подъёмная сила корпуса при малых углах атаки создаётся только на тех участках, где изменяется площадь поперечного сечения 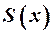 , т. е. при
, т. е. при 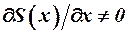 . При положительном угле атаки на носовой и расширяющейся кормовой частях (
. При положительном угле атаки на носовой и расширяющейся кормовой частях ( ) создаётся положительная подъёмная сила, а на сужающейся кормовой части (
) создаётся положительная подъёмная сила, а на сужающейся кормовой части (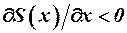 ) – отрицательная. На цилиндрической части (
) – отрицательная. На цилиндрической части ( ) подъёмная сила не создаётся.
) подъёмная сила не создаётся.
Более точные теории, а также экспериментальные данные показывают, что теория тонкого тела даёт качественно правильные результаты при малых углах атаки только для носовой и цилиндрической частей корпуса при дозвуковых скоростях полёта. Эта теория не учитывает возникновения подъёмной силы на цилиндрической части в сверхзвуковом потоке, а также уменьшения по абсолютной величине подъёмной силы кормы из-за наличия пограничного слоя. Она также не учитывает возникновения дополнительной силы на корпусе при больших углах атаки.
В дозвуковом потоке коэффициент 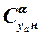 заострённой носовой части можно определить по формуле
заострённой носовой части можно определить по формуле
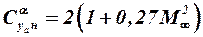 , (3.12)
, (3.12)
независимо от её конфигурации. Положение фокуса носовой части не очень малого удлинения при дозвуковых скоростях довольно точно определяется по теории тонкого тела:
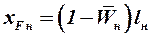 . (3.13)
. (3.13)
Величина относительного объёма  для некоторых носовых частей приведена в подразд. 1.1. Вычисленные по формуле (3.13) значения фокуса носовой части могут быть использованы в качестве первого приближения и при сверхзвуковых скоростях.
для некоторых носовых частей приведена в подразд. 1.1. Вычисленные по формуле (3.13) значения фокуса носовой части могут быть использованы в качестве первого приближения и при сверхзвуковых скоростях.
 Значения производных
Значения производных 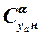 для конических и оживальных головок при сверхзвуковых скоростях полёта могут быть определены по графику на рис. 3.1. Следует обратить внимание на значительное увеличение коэффициента
для конических и оживальных головок при сверхзвуковых скоростях полёта могут быть определены по графику на рис. 3.1. Следует обратить внимание на значительное увеличение коэффициента 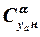 криволинейной носовой части вследствие взаимодействия поверхности с носовой ударной волной.
криволинейной носовой части вследствие взаимодействия поверхности с носовой ударной волной.
Цилиндрическая часть корпуса при малых углах атаки в дозвуковом потоке не создаёт подъёмной силы, т. е. 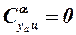 . При сверхзвуковых скоростях полёта возмущения, распространяющиеся со всех точек криволинейной носовой части и от места стыка конической носовой части с цилиндрической, отражаются от головного скачка уплотнения, дополнительно искривляя его, и попадают на цилиндрическую часть. При наличии угла атаки эта картина становится несимметричной, что приводит к перераспределению подъёмной силы на криволинейных носовых частях и к образованию подъёмной силы на цилиндрической части корпуса.
. При сверхзвуковых скоростях полёта возмущения, распространяющиеся со всех точек криволинейной носовой части и от места стыка конической носовой части с цилиндрической, отражаются от головного скачка уплотнения, дополнительно искривляя его, и попадают на цилиндрическую часть. При наличии угла атаки эта картина становится несимметричной, что приводит к перераспределению подъёмной силы на криволинейных носовых частях и к образованию подъёмной силы на цилиндрической части корпуса.
При сверхзвуковых скоростях полёта величина производной 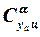 и положение фокуса
и положение фокуса  могут быть определены по графикам, представленным на рис. 3.2.
могут быть определены по графикам, представленным на рис. 3.2.

Эти значения также могут быть определены по формулам
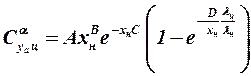 , (3.14)
, (3.14)
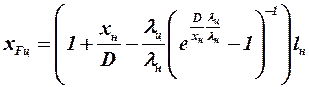 , (3.15)
, (3.15)
где  , а коэффициенты
, а коэффициенты 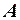 ,
, 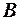 ,
,  и
и  для конической и оживальной (сопряжение с цилиндрической частью выполнено по касательной) носовых частей приведены в табл. 3.1.
для конической и оживальной (сопряжение с цилиндрической частью выполнено по касательной) носовых частей приведены в табл. 3.1.
Таблица 3.1
| Носовая часть | A | B | C | D |
| Конус | 1,3 | 0,5 | 0,05 | 1,29 |
| Оживало | 4,5 | 3,0 | 1,5 | 0,88 |
Величину производной  для кормовой части приближённо можно определить по следующей формуле:
для кормовой части приближённо можно определить по следующей формуле:
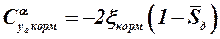 , (3.16)
, (3.16)
где коэффициент  учитывает изменение подъёмной силы кормовой части из-за наличия пограничного слоя (при
учитывает изменение подъёмной силы кормовой части из-за наличия пограничного слоя (при  приведенная формула даёт значения, соответствующие теории тонкого тела). Для сужающейся кормовой части влияние пограничного слоя значительно больше (
приведенная формула даёт значения, соответствующие теории тонкого тела). Для сужающейся кормовой части влияние пограничного слоя значительно больше ( ), чем для расширяющейся (
), чем для расширяющейся (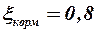 ).
).
Если длина кормовой части значительно меньше длины корпуса, то можно считать, что её фокус по углу атаки расположен на середине её длины и его положение не зависит от числа  :
:
 . (3.17)
. (3.17)
Следует обратить внимание на то, что эти аэродинамические характеристики кормовой части не зависят в первом приближении от числа  .
.
Полученные данные позволяют определить коэффициенты 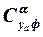 и
и  по формулам (3.10) и (3.11). Необходимо отметить, что фокус корпуса при сужающейся кормовой части может быть расположен впереди носовой части.
по формулам (3.10) и (3.11). Необходимо отметить, что фокус корпуса при сужающейся кормовой части может быть расположен впереди носовой части.
3.3. Производные от коэффициентов подъёмной силы
и продольного момента изолированных несущих поверхностей
по углу атаки при 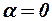
Как уже упоминалось выше, при расчёте аэродинамических характеристик несущих поверхностей, установленных на ЛА, необходимо учитывать их интерференцию с корпусом, а также с другими несущими поверхностями.
Обширные теоретические и экспериментальные исследования посвящены изучению обтекания и получению аэродинамических характеристик изолированных несущих поверхностей. Большинство теоретических методов разработано для тонких несущих поверхностей. Наиболее общей расчётной схемой, моделирующей обтекание изолированной несущей поверхности при дозвуковых скоростях, является её замена вихревой поверхностью. В основе теоретических исследований несущих поверхностей при сверхзвуковых скоростях лежат нелинейные дифференциальные уравнения газовой динамики. Здесь для расчёта обтекания наиболее разработанными являются методы Е. А. Красильщиковой, Аккерета и теория конических течений.
Как показывают эти исследования, производная от коэффициента подъёмной силы по углу атаки и положение фокуса изолированной несущей поверхности зависят от числа  и формы поверхности в плане. Однако при дозвуковых и особенно при трансзвуковых скоростях эти параметры зависят также от формы профиля и, в частности, от его относительной толщины. Используя параметры подобия для изолированной несущей поверхности, можно записать
и формы поверхности в плане. Однако при дозвуковых и особенно при трансзвуковых скоростях эти параметры зависят также от формы профиля и, в частности, от его относительной толщины. Используя параметры подобия для изолированной несущей поверхности, можно записать
 ,
,  . (3.18)
. (3.18)
Графики этих зависимостей для  приведены на рис. 3.3 [8].
приведены на рис. 3.3 [8].
Так как сужение несущей поверхности мало влияет на величину производной  , то параметр
, то параметр 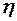 на графиках не показан, а приведенные данные являются осреднёнными для различных значений сужения. На режимах течения, при которых кромки несущей поверхности переходят от дозвукового типа обтекания к сверхзвуковому, теоретические расчёты указывают на наличие изломов в поведении кривых
на графиках не показан, а приведенные данные являются осреднёнными для различных значений сужения. На режимах течения, при которых кромки несущей поверхности переходят от дозвукового типа обтекания к сверхзвуковому, теоретические расчёты указывают на наличие изломов в поведении кривых  . На приведенных графиках эти изломы сглажены в соответствии с экспериментальными данными.
. На приведенных графиках эти изломы сглажены в соответствии с экспериментальными данными.


В дозвуковом потоке при больших значениях приведенного удлинения для определения  можно использовать формулу
можно использовать формулу
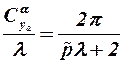 , (3.19)
, (3.19)
где  – отношение полупериметра кромок несущей поверхности к её размаху. Для поверхности с прямолинейными передними и задними кромками и с концевой хордой, параллельной бортовой,
– отношение полупериметра кромок несущей поверхности к её размаху. Для поверхности с прямолинейными передними и задними кромками и с концевой хордой, параллельной бортовой,
 (3.20)
(3.20)
С учётом сжимаемости необходимо пользоваться следующей формулой [13]:
 . (3.21)
. (3.21)
В приведенных формулах 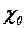 и
и 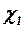 – углы стреловидности передней и задней кромок поверхности.
– углы стреловидности передней и задней кромок поверхности.
В сверхзвуковом потоке при больших значениях приведенного удлинения величина  слабо зависит от формы поверхности в плане и приближается к аналогичному значению для профиля, т. е.
слабо зависит от формы поверхности в плане и приближается к аналогичному значению для профиля, т. е.
 (3.22)
(3.22)
Эти значения показаны на рис. 3.3 пунктиром.
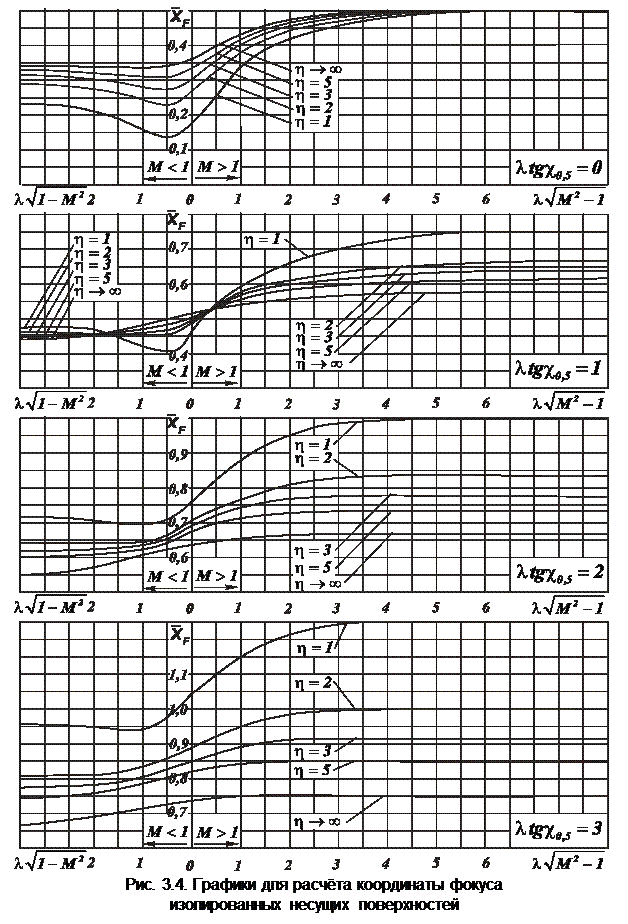
Линейная теория крыльев конечного размаха позволяет рассчитать положение их фокуса при дозвуковых и сверхзвуковых скоростях. Скорректированные экспериментальными данными результаты для плоских крыльев с симметричными профилями приведены на рис. 3.4. Здесь координата фокуса отнесена к центральной или бортовой хорде поверхности, составленной из консолей, и отсчитывается от её начала. Следует помнить, что эти графики в околозвуковой области имеют качественный характер, так как из-за недостатка экспериментальных данных пока не удаётся выяснить влияние параметра  на положение фокуса в этой области. Некоторые данные о влияние этого параметра на положение фокуса прямоугольных крыльев в трансзвуковой области приведены в работе [8]. Кривые, представленные на графиках, соответствуют значениям
на положение фокуса в этой области. Некоторые данные о влияние этого параметра на положение фокуса прямоугольных крыльев в трансзвуковой области приведены в работе [8]. Кривые, представленные на графиках, соответствуют значениям  .
.
Положение фокуса несущей поверхности для дозвуковых скоростей при больших значениях приведенного удлинения можно приближённо определить по формуле [13]
 , (3.23)
, (3.23)
где 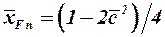 – фокус профиля.
– фокус профиля.
В сверхзвуковом потоке при больших значениях приведенного удлинения координата фокуса поверхности стремится к положению центра тяжести площади поверхности в плане:
 . (3.24)
. (3.24)
Здесь  и
и 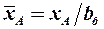 , где
, где  – величина средней аэродинамической хорды;
– величина средней аэродинамической хорды;  – величина бортовой хорды;
– величина бортовой хорды; 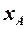 – расстояние между началами бортовой и средней аэродинамической хордами.
– расстояние между началами бортовой и средней аэродинамической хордами.
Найденные величины позволяют определить производную от коэффициента продольного момента несущей поверхности по углу атаки:
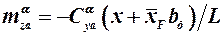 , (3.25)
, (3.25)
где  – расстояние от носика части ЛА до начала бортовой хорды рассматриваемой поверхности.
– расстояние от носика части ЛА до начала бортовой хорды рассматриваемой поверхности.
Аэродинамические характеристики несущих поверхностей определяются с учётом торможения потока, т. е. 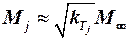 .
.
|
|
|
|
|
Дата добавления: 2014-12-26; Просмотров: 3391; Нарушение авторских прав?; Мы поможем в написании вашей работы!