Общий вид транспортной матрицы задачи о назначениях

Транспортная задача и ее реализация

Транспортная задача является одной из наиболее распространенных задач линейного программирования и нахо­дит широкое практическое приложение.

Постановка транспортной задачи. Некоторый однородный про­дукт, сосредоточенный у 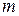поставщиков 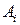в количестве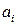 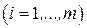единиц, необходимо доставить 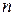потребителям 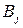в количе­стве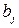 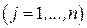единиц. Известна стоимость 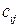перевозки единицы груза от поставщика 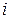к потребителю 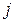. Составить план перевозок, позволяющий с минимальными затратами вывести все грузы и полностью удовлетворить потребителей.

Сформулируем экономико-математическую модель транспортной задачи. Обозначим через 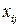количество единиц груза, запланиро­ванных к перевозке от поставщика 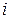к потребителю 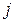. Так как от поставщика 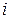к потребителю 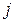запланировано перевезти 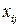единиц груза, то стоимость перевозки составит .

Транспортная задача относится к двух индексным задачам ли­нейного программирования, так как в результате решения задачи необходимо найти матрицу 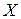с компонентами .

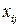Стоимость всего плана выразится двойной суммой

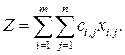
Систему ограничений получаем из следующих условий задачи:

1) все грузы должны быть перевезены, т.е.

;

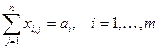2) все потребности должны быть удовлетворены, т.е.

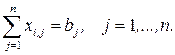
Таким образом, математическая модель транспортной задачи имеет следующий вид. Найти минимальное значение линейной функции

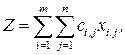
при ограничениях

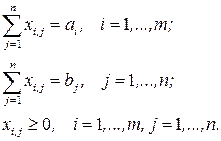
В рассмотренной модели предполагается, что суммарные за­пасы равны суммарным потребностям, т.е.

;

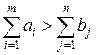Транспортная задача, в которой суммарные запасы и потреб­ности совпадают, т.е. выполняется условие (4.20), называется за­крытой моделью; в противном случае – открытой.

Для открытой модели может быть два случая:

1) суммарные запасы превышают суммарные потребности :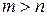

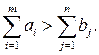
2) суммарные потребности превышают суммарные запасы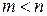

Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений.

Задача заключается в нахождении минимального значения линейной функции

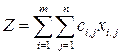
при ограничениях в случае (1):

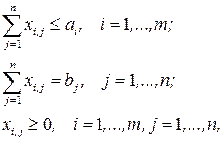
при ограничениях в случае (2):

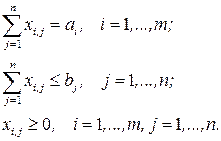
Открытая модель решается приведением к закрытой модели. В случае (1), когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель 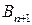, потребность, которая описывается формулой:

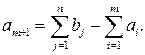
Для случая (2), когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик 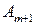запа­сы которого описываются выражением:

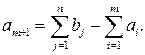
Стоимость перевозки единицы груза до фиктивного потребителя и стоимость перевозки груза от фиктивного поставщика полагают­ся равными нулю, так как груз в обоих случаях не перевозится.

Транспортная задача состоит из 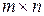уравнений с 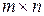неизвест­ными.

Матрицу перевозок 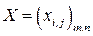, удовлетворяющую услови­ям (4.24)–(4.25), называют планом перевозок транспортной задачи, а 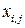– перевозками.

План 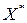, при котором целевая функция (4.23) обращается в минимум, называется оптимальным.

4.6. Применение транспортных моделей
к решению некоторых экономических задач

Алгоритм и методы решения транспортной задачи могут быть использованы при решении некоторых экономичес­ких задач, не имеющих ничего общего с транспортировкой груза. В этом случае величины тарифов 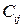имеют различный смысл в зависимости от конкретной экономической задачи.

К таким за­дачам относятся:

· оптимальное закрепление за станками операций по
обработке деталей. В них 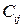является таким экономическим показателем, как производительность. Задача позволяет определить, сколько времени и на какой операции нужно использовать каж­дый из станков, чтобы обработать максимальное количество деталей;

· оптимальные назначения, или проблема выбора. Имеется 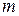ме­ханизмов, которые могут выполнять 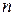различных работ с про­изводительностью 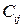. Задача позволяет определить, какой ме­ханизм и на какую работу надо назначить, чтобы добиться максимальной производительности;

· задача о сокращении производства с учетом суммарных рас­ходов на изготовление и транспортировку продукции;

· задача о закреплении самолетов за воздушными линиями;

· решение задач с помощью метода запрещения перевозок. Метод используется в том случае, если груз от некоторого поставщи­ка по каким-то причинам не может быть направлен одному из потребителей. Данное ограничение можно учесть, присвоив со­ответствующей клетке достаточно большое значение стоимос­ти, тем самым в эту клетку не будут производиться перевозки.

4.7. Задача о назначениях

Задача о назначениях – это распределительная за­дача, в которой для выполнения каждой работы требуется один и только один ресурс (один человек, одна автомашина и т.д.) и каждый ресурс может быть использован на одной и только одной работе. То есть ресурсы неделимы между работами, а работы не­делимы между ресурсами. Таким образом, задача о назначениях является частным случаем транспортной задачи. Задача о назна­чениях имеет место при распределении людей на должности или работы, автомашин – на маршруты, водителей – на машины, групп – по аудиториям, научных тем – по научно-исследовательским лабораториям и т.п.

Исходные параметры задачи о назначениях:

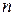- – количество ресурсов;

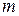- – количество работ;

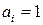- – единичное количество ресурса 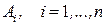(напри­мер, один работник, одно транспортное средство, одна научная тема и т.д.);

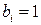- – единичное количество работы 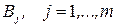(напри­мер, одна должность, один маршрут, одна лаборатория);

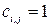- – характеристика качества выполнения работы 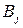, с помо­щью ресурса 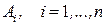, (например, компетентность работника 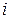при работе на должности 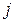; время, за которое транспортное средство 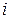пере­везет груз по маршруту 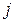; степень квалификации лаборатории 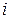при работе над научной темой ).

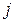Искомые параметры:

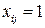- –факт назначения или не назначения ресурса, 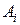, 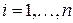на ра­боту , :

-

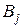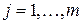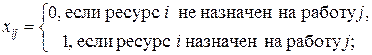
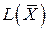- – общая (суммарная) характеристика качества распреде­ления ресурсов по работам.

Общий вид транспортной матрицы задачи представлен в табл. 4.2.

Таблица 4.2

Ресурсы	Работы	Количество ресурсов
...
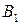
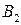
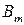
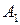
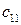
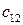
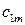
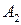
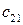
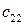
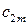
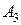
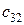
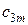
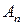
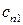
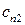
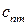
Количество работ

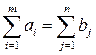
Экономико-математическая модель задачи формулируется как

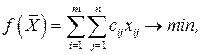
при ограничениях:

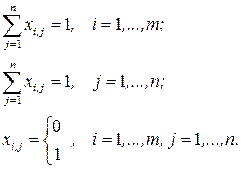
По сравнению с транспортной задачей процесс приведения задачи о назначениях к сбалансированному виду имеет свои осо­бенности (принимают значение «0» или «1»). При решении задач о назначении в Excel необходимо учиты­вать, что переменные 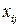являются булевыми.

5. Балансовые модели

Эффективное функционирование экономики пред­полагает наличие баланса между отдельными отраслями.

Каждая отрасль при этом выступает, с одной стороны, как производитель некоторой продукции, а с другой — как потребитель продуктов, вырабатываемых другими отраслями.

Для наглядного выражения взаимной связи между отраслями используют таблицы определен­ного вида, которые называют таблицами межотраслевого баланса. Впервые эти таблицы были опубликованы в 1926 г., в России.

Математическая модель межотраслевого баланса (МОБ), допуска­ющая широкие возможности анализа и прогноза, появилась позже (1936 г.) в трудах американского экономиста Василия Васильевича Леонтьева. В 1973 г. В.В. Леонтьев был удостоен премии Альфреда Нобеля по экономике за развитие и применение данных моделей.

Дата добавления: 2014-12-26