Текущая стоимость единицы

Более частое накопление

Нередко период накопления короче года. Накопление может происхо­дить ежедневно, раз в месяц, в квартал или в полгода. Обычно устанав­ливается номинальная годовая ставка, например 10%, однако при более частом накоплении эффективная ставка процента повышается. Общая формула остается той же:

Sⁿ =(1 + Е)ⁿ,

однако с учетом сокращения периода накопления в нее должны быть внесены изменения.

При корректировке данной формулы число лет, на протяжении ко­торых происходит накопление, умножается на его частоту в течение од­ного года; одновременно номинальная годовая ставка процента делит­ся на частоту накопления. Результат покажет эффективную ставку про­цента за период накопления.

Пример 3.3. Вклад в сумме 1000руб. размещен на 1 год под 10 % годовых. Проценты начисляются ежеквартально. Необходимо опре­делить: периодическую ставку процента, будущую стоимость вкла­да, доход на капитал (Д).

Решение:

1.

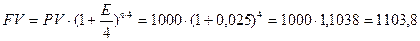
2. Доход = 1103,8 - 1000 = 103,8 руб.

Текущая стоимость единицы (реверсии)— это величина обратная накопленной сумме единицы. Это текущая стоимость одного доллара, который должен

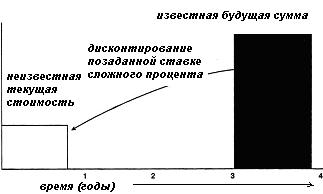
Рис. 3.2. Текущая стоимость реверсии

быть получен в будущем. Поскольку целью осуществле­ния инвестиций является получение доходов в будущем, умножение фа­ктора текущей стоимости реверсии на величину ожидаемого будущего дохода является важнейшим шагом в оценке инвестиций.

Текущая стоимость реверсии (Vⁿ)описана графически на рис. 3.2. Данный коэффициент используется для оценки текущей стоимости из­вестной (или прогнозируемой) суммы будущего единовременного по­ступления денежных средств с учетом заданного процента. При приме­нении фактора текущей стоимости используются понятия дисконтиро­вание (discounting) или ставка дисконта (discount rate), противоположные понятиям накопление (compounding) и ставка процента (interest rate), применяемым при расчете накопленной суммы единицы.

Поскольку деньги обладают стоимостью во времени, один доллар, который будет получен в будущем, стоит меньше доллара, получаемого сегодня. Насколько меньше (сумма дисконта), зависит от:

а) разрыва во времени между оттоком и притоком денежных средств и

б) необходи­мой ставки процента или дисконта.

Например, при 10%-ной ставке процента (ставке дисконта) текущая стоимость 100,00 долл., ожидаемых к получению через год, равна 90,91 долл. Арифметическая проверка: если сегодня инвестор вкладывает 90,91 долл. и в течение следующего года может получить чистый доход в 9>09 долл., то процент составит 9,09 долл.; поэтому через год основ­ная сумма инвестиций, включая добавленный процент, будет равна 100,00 долл. (90,91 долл. + 9,09 долл. = 100,00 долл.).

Инвестор, который рассчитывает получить через два года 100,00 долл. и вкладывает сегодня 82,64 долл., получит 10%-ную годовую ставку. Проверка: при 10%-ной годовой ставке 82,64 долл. превратятся через год в 90,91 долл., а через 2 года — в 100,00 долл.

Поэтому формула текущей стоимости денег:

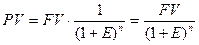
где: где: FV- будущая стоимость денег;

PV- текущая стоимость денег;

(1+E)ⁿ – фактор сложного процента;

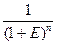- коэффициент текущей стоимости.

Формула расчета коэффициента текущей стоимости (реверсии) имеет следующий вид:

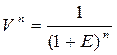
Данный фактор является обратной величиной от накопленной суммы единицы. Поэтому любая задача, которая может быть решена с использованием фактора накопленной суммы единицы, может быть также решена с применением фактора реверсии, однако не через умножение, а через деление.

Например, как показано ранее, 100,00 долл., накапливаемые по сложной ставке 10%, через пять лет возрастут до 161,05 долл. Посколь­ку 100,00 долл. через пять лет превратятся в 161,05 долл., то 62,05 долл. — это та сумма, которая за пять лет возрастет до 100,00 долл.

Пример 3.4. Покупатель земельного участка рассчитывает пе­репродать его через 7 лет за 100 000 рублей. Какова максимальная сумма, которую он может предложить продавцу, если хочет, что­бы его годовой доход составил 15 %?

Решение:

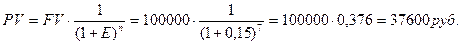
Дата добавления: 2014-12-26