Рекурсия

В теле функции известны все объекты, описанные во внешнем блоке, т.е. все глобальные переменные и имя самой функции.

Таким образом, внутри любой функции можно вызывать любую доступную функцию, в том числе и саму себя. Ситуация, когда функция вызывает саму себя, называется рекурсия.

Рекурсия возможна благодаря тому, что при вызове функции создаются новые экземпляры локальных переменных, которые сохраняются во внутреннем стеке машины. Стек функционирует по принципу LIFO - Last In – First Out (последний вошел – первый вышел).

Переменные помещаются в стек одна за другой и выбираются из стека в обратном порядке.

Обязательным элементом всякого рекурсивного процесса является утверждение, определяющее условие завершения рекурсии. Оно называется опорным условием рекурсии.

Если опорное условие выполняется, то может быть задано некоторое фиксированное значение, заведомо достижимое в ходе вычисления. Это позволит организовать своевременную остановку рекурсивного процесса.

Рассмотрим пример вычисления факториала 5.

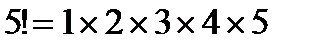, где 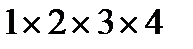- это 4!

Т.е 5!=4! 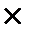5

Факториал нуля равен 1. Отсюда формула вычисления N-факториала:

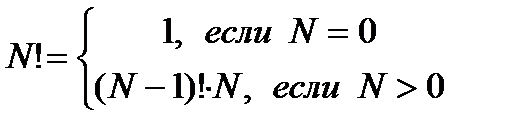
Реализуем вычисление факториала в виде функции:

#include "stdafx.h"

float fact(int n)

{

if (n==0)

return 1;

else

return (fact(n-1)*n);

}

void main()

{

printf("факториал 5=%f\n",fact(5));

}

Дата добавления: 2014-12-26