Массовые силы

Силы, действующие в жидкости

Массовые силы это силы, пропорциональные массе жидкости. В случае однородной жидкости эти силы пропорциональны объёму. Прежде всего, к ним относится вес жидкости

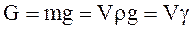, (22)

где G – вес жидкости,

V – объём жидкости,

m – масса жидкости,

g – ускорение свободного падения,

ρ – плотность жидкости,

γ – удельный вес жидкости.

Как известно, масса является мерой инертности тела. Это свойство присуще и жидкостям, поэтому к массовым силам относятся и силы инерции:

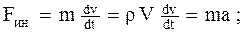(23)

где F_ин– инерционная сила,

v– скорость жидкости,

t – время движения,

a – ускорение движения.

Силы инерции, действующие в жидкости, так же как и для твёрдого тела, могут проецироваться на оси.

2.1.2 Поверхностные силы

Поверхностные силы – силы, величины которых пропорциональны площади. К ним относят два вида сил. Силы поверхностного натяжения и силы вязкого трения. Последние проявляются только при движении жидкости и не играют никакой роли, когда жидкость находится в покое. Эти силы, как свойство вязкости, были рассмотрены при изучении свойств жидкостей.

2.1.3 Силы поверхностного натяжения

Молекулы жидкости притягиваются друг к другу с определённой силой. Причём внутри жидкости силы, действующие на любую молекулу, уравновешиваются, т.к. со всех сторон от неё находятся одинаковые молекулы, расположенные на одинаковом расстоянии. Однако молекулы жидкости, находящиеся на границе (с газом, твердым телом или на границе двух несмешивающихся жидкостей) оказываются в неуравновешенном состоянии т.к. со стороны другого вещества действует притяжение других молекул, расположенных на других расстояниях. Возникает преобладание какой-то силы. Под влиянием этого воздействия поверхность жидкости стремится принять форму, соответствующую наименьшей площади. Если силы внутри жидкости больше наружных сил, то поверхность жидкости стремится к сферической форме. Например, малые массы жидкости в воздухе стремятся к шарообразной форме, образуя капли. Может иметь место и обратное явление, которое наблюдается как явление капиллярности. В трубах малого диаметра (капиллярах) наблюдается искривление свободной поверхности, граничащей с газом или с парами этой же жидкости. Если поверхность трубки смачивается, свободная поверхность жидкости в капилляре вогнутая. Если нет смачивания, свободная поверхность выпуклая, как при каплеобразовании. Во всех этих случаях силы поверхностного натяжения обусловливают дополнительные напряжения p_пов в жидкости. Величина этих напряжений определяется формулой

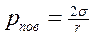. (24)

где σ - коэффициент поверхностного натяжения,

r - радиус сферической поверхности, которую принимает жидкость.

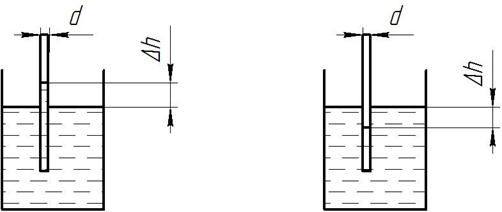
Рисунок 5 – Капиллярное поднятие и опускание жидкости

Эти дополнительные напряжения легко наблюдать, если в сосуд с жидкостью погрузить капилляр. В этом опыте возможны два варианта. В первом случае жидкость, за счёт поверхностных сил, поднимется по капилляру на некоторую высоту. Тогда говорят о капиллярном поднятии, и наблюдается явление смачивания.

Во втором варианте жидкость опускается в капилляре ниже уровня жидкости в сосуде. Такое явление называют капиллярным опусканием, которое происходит при несмачивании.

В обоих случаях величина 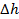пропорциональна дополнительному напряжению, вызванному в жидкости поверхностными силами. Она равна

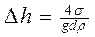; (25)

где σ - коэффициент поверхностного натяжения,

d – диаметр капилляра,

k – коэффициент пропорциональности, который выражается следующей формулой и зависит от жидкости. Например, при t = 20 ºC, k спирта составляет 11,5, ртути – 10,15 а воды - 30.

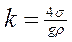, (26)

Поднятие воды в капиллярах почвы и грунтов является важным фактором в распространении воды. Высота капиллярного поднятия в грунтах изменяется от нуля (галечники) почти до 5 м (глины). При этом с увеличением минерализации воды высота капиллярного поднятия увеличивается.

Поверхностное натяжение и капиллярные эффекты определяют закономерности движения жидкости в условиях невесомости.

К поверхностным силам относятся и силы давления, т.к. они действуют на поверхности жидкости.

2.1.4 Силы давления

Давление – напряжение, возникающее в жидкости под действием сжимающих сил.

Рассмотрим объем жидкости, находящейся в равновесии (рис.).

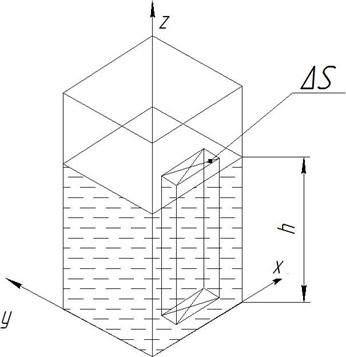
Рисунок 6 – Схема для определения сил давления

Выделим внутри этой жидкости на глубине h горизон­тальную элементарную площадку DS, параллельную свободной поверхности жидкости.(Свободной называют поверхность находящуюся на границе раздела жидкости и газа.) Спроектировав эту площадку на свобод­ную поверхность жидкости, получим вертикальный параллелепипед, у которого нижнее основание — площадка DS, а верхнее — ее проекция DS', при этом DS = DS'. На площадку DS действует сила гидростатического давления DР, равная произведению массы выделенного столба (параллелепипеда) жидкости на уско­рение свободного падения:

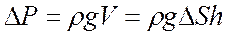(27)

Отношение силы DР к площадке DS, на которую она действу­ет, представляет собой силу, действующую на единицу площади и называется средним гидростатическим давлением или средним напряжением гидростатического давления по площади DS:

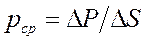(28)

Истинное давление Р в различных точках этой площадки DS может быть различным; Р ср будет тем меньше отличаться от действительного в точке, чем меньше будет площадь DS. Таким образом, если размер площадки DS уменьшать, приближать к нулю, то отношение DР /DS будет стремиться к некоторому пре­делу, выражающему истинное гидростатическое давление в точке:

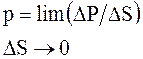(29)

Гидростатическое давление Р (Па) измеряют в единицах силы, деленных на единицу площади, оно характеризуется тремя основными свойствами. Если давление отсчитывается от нуля, оно называется абсолютным и обозначается , если от атмосферного, – избыточным и обозначается 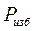. Атмосферное давление обозначается .

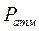Кроме того, различают давление гидродинамическое и гидростатическое. Гидродинамическое давление возникает в движущейся жидкости. Гидростатическое давление – давление в покоящейся жидкости.

2.2 Свойства гидростатического давления

Первое свойство. Гидростатическое давление направлено всег­да по внутренней нормали к по­верхности, на которую оно дей­ствует.

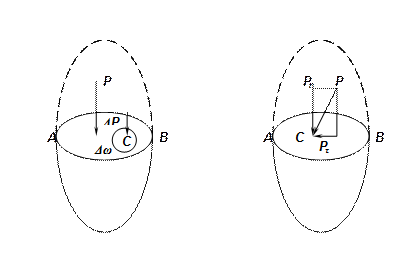
Рисунок 7 – схема для определения перевого свойства гидростатического давления

Рассмотрим силу гидростатического давления Р, приложен­ную в точке С под углом к поверхности А—В объема жидкости, находящегося в покое (рис.). Тогда эту силу можно разло­жить на две составляющие: нормальную Рп и касательную Рt к поверхности А—В. Касательная составляющая—это равно­действующая сил трения, приходящихся на выделенную поверх­ность вокруг точки С. Но так как жидкость находится в покое, то силы трения отсутствуют, т. е. Рt =0.

Следовательно, сила гидростатического давления Р в точке С действует лишь в направлении силы Рп, т. е. нормально к по­верхности А—В. Причем направлена она только по внутренней нормали. При предположении направления силы гидростатиче­ского давления по внешней нормали возникнут растягивающие усилия, что приведет жидкость в движение. А это противоречит условию. Таким образом, сила гидростатического давления всег­да сжимающая, т. е. направлена но внутренней нормали.

Второе свойство состоит в том, что в любой точке внутри жидкости давление по всем направлениям одинаково. Иначе это свойство давления звучит так: на любую площадку внутри объёма жидкости, независимо от её угла наклона, действует одинаковое давление.

Докажем второе свойство..

Рисунок 8 – схема для определия второго свойствав гидростатичекого давления

Для доказательства этого свойства выделим в жидкости, на­ходящейся в равновесии, частицу в форме треугольной призмы с основанием в виде прямоугольного треугольника А—В—С. Будем рассматривать этот объём в некоторой произвольной системе координат X, Y, Z. При этом ось у перпендикулярна плоскости. Заме­ним действие жидкости вне призмы на ее боковые грани гидростатическим давлением соответственно Pх, Pz, Pе.

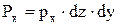
(30)

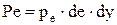
Кроме этих сил на призму действует сила тяжести dG, рав­ная весу призмы g*dz*dx*dy/2.

Силой тяжестью можно пренебречь. Так как она будет величиной 3-го порядка малости, а силы действующие на грани призмы 2 –го порядка малости.

Так как частица жидкости находится в равновесии, в покое, то сумма проекций всех сил, приложен­ных к ней, на любое направление равна нулю т.е.

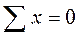
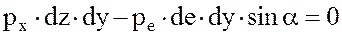(31)

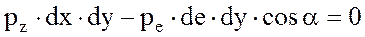
Подставляя dz=de sina и dx=de cosa в предыдущие уравнения и разделив каждое уравнение dy, по­лучим

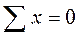
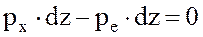
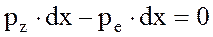
Из выражений следует

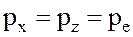(32)

Следовательно, гидростатическое давление на наклонную грань Р е одинаково по величине с гидростатическим давлением на вертикальную и горизонтальную грани. Так как угол наклона грани a взят произвольно, то можно утверждать, что гидростати­ческое давление в любой точке жидкости действует одинаково по всем направлениям.

Третье свойство. Гидростатическое давление в точке зави­сит только от ее координат в пространстве, т. е.

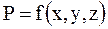
Это свойство не требует специального доказательства, так как очевидно, что по мере увеличения заглубления точки под вровень давление в ней будет возрастать и, наоборот, по мере уменьшения заглубления — уменьшаться.

Дата добавления: 2014-12-26