Дискриминантные функции для нескольких групп

Интерпретация функции дискриминации для двух групп

Для двух групп дискриминантный анализ (в литературе обозначается линейным дискриминантным анализом Фишера) может рассматриваться также как процедура множественной регрессии (с вычислительной точки зрения эти подходы аналогичны). Если вы кодируете две группы как 1 и 2, и затем используете эти переменные в качестве зависимых переменных в множественной регрессии, то получите результаты, аналогичные тем, которые получили бы с помощью Дискриминантного анализ а. В общем, в случае двух совокупностей вы подгоняете линейное уравнение следующего типа:

Группа = a + b₁*x₁ + b₂*x₂ +... + b_m*x_m

где a является константой, и b₁... b_m являются коэффициентами регрессии. Интерпретация результатов задачи с двумя совокупностями тесно следует логике применения множественной регрессии: переменные с наибольшими регрессионными коэффициентами вносят наибольший вклад в дискриминацию.

Если имеется более двух групп, то можно оценить более, чем одну дискриминантную функцию. Например, когда имеются три совокупности, вы можете оценить: (1) - функцию для дискриминации между совокупностью 1 и совокупностями 2 и 3, взятыми вместе, и (2) - другую функцию для дискриминации между совокупностью 2 и совокупности 3. Например, вы можете иметь одну функцию, дискриминирующую между теми выпускниками средней школы, которые идут в колледж, против тех, кто этого не делает (но хочет получить работу или пойти в училище), и вторую функцию для дискриминации между теми выпускниками, которые хотят получить работу против тех, кто хочет пойти в училище. Коэффициенты b в этих дискриминирующих функциях могут быть проинтерпретированы тем же способом, что и ранее.

Канонический анализ. Когда проводится дискриминантный анализ нескольких групп, можно не указывать, каким образом следует комбинировать группы для формирования различных дискриминирующих функций. Вместо этого, вы можете автоматически определить некоторые оптимальные комбинации переменных, так что первая функция проведет наилучшую дискриминацию между всеми группами, вторая функция будет второй наилучшей и т.д. Более того, функции будут независимыми или ортогональными, то есть их вклады в разделение совокупностей не будут перекрываться. С вычислительной точки зрения система проводит анализ канонических корреляций, которые будут определять последовательные канонические корни и функции. Максимальное число функций будет равно числу совокупностей минус один или числу переменных в анализе в зависимости от того, какое из этих чисел меньше.

Интерпретация дискриминантных функций. Как и в случае регрессии, вы получите коэффициенты b (и стандартизованные коэффициенты бета) для каждой переменной и для каждой дискриминантной (теперь называемой также и канонической) функции. Они могут быть также проинтерпретированы обычным образом: чем больше стандартизованный коэффициент, тем больше вклад соответствующей переменной в дискриминацию совокупностей. Однако эти коэффициенты не дают информации о том, между какими совокупностями дискриминируют соответствующие функции. Вы можете определить характер дискриминации для каждой дискриминантной (канонической) функции, взглянув на средние функций для всех совокупностей. Вы также можете посмотреть, как две функции дискриминируют между группами, построив значения, которые принимают обе дискриминантные функции.

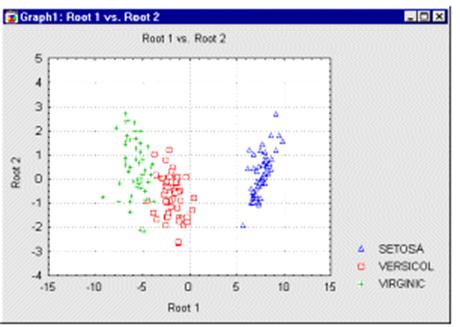
В этом примере Корень1 (root1), похоже, в основном дискриминирует между группой Setosa и объединением групп Virginic и Versicol. По вертикальной оси (Корень2) заметно небольшое смещение точек группы Versicol вниз относительно центральной линии (0).

Матрица факторной структуры. Другим способом определения того, какие переменные "маркируют" или определяют отдельную дискриминантную функцию, является использование факторной структуры. Коэффициенты факторной структуры являются корреляциями между переменными в модели и дискриминирующей функцией (можно рассматривать эти корреляции как факторные нагрузки переменных на каждую дискриминантную функцию).

Некоторые авторы согласны с тем, что структурные коэффициенты могут быть использованы при интерпретации реального "смысла" дискриминирующей функции. Основания заключаются в том, что: (1) - вероятно структура коэффициентов более устойчива и (2) - они позволяют интерпретировать факторы (дискриминирующие функции) таким же образом, как и в факторном анализе. Однако последующие исследования с использованием метода Монте-Карло (Барсиковский и Стивенс (Barcikowski, Stevens, 1975); Хьюберти (Huberty, 1975)) показали, что коэффициенты дискриминантных функций и структурные коэффициенты почти одинаково нестабильны, пока значение размера выборки не станет достаточно большим (например, если число наблюдений в 20 раз больше, чем число переменных). Важно помнить, что коэффициенты дискриминантной функции отражают уникальный (частный) вклад каждой переменной в отдельную дискриминантную функцию, в то время как структурные коэффициенты отражают простую корреляцию между переменными и функциями. Если дискриминирующей функции хотят придать отдельные "осмысленные" значения (родственные интерпретации факторов в факторном анализе), то следует использовать (интерпретировать) структурные коэффициенты. Если же хотят определить вклад, который вносит каждая переменная в дискриминантную функцию, то используют коэффициенты (веса) дискриминантной функции.

Значимость дискриминантной функции. Можно проверить число корней, которое добавляется значимо к дискриминации между совокупностями. Для интерпретации могут быть использованы только те из них, которые будут признаны статистически значимыми. Остальные функции (корни) должны быть проигнорированы.

Итак, при интерпретации дискриминантной функции для нескольких совокупностей и нескольких переменных, вначале хотят проверить значимость различных функций и в дальнейшем использовать только значимые функции. Затем, для каждой значащей функции следует рассмотреть для каждой переменной стандартизованные коэффициенты бета. Чем больше стандартизованный коэффициент бета, тем большим является относительный собственный вклад переменной в дискриминацию, выполняемую соответствующей дискриминантной функцией. В порядке получения отдельных "осмысленных" значений дискриминирующих функций можно также исследовать матрицу факторной структуры с корреляциями между переменными и дискриминирующей функцией. В заключение, стоит посмотреть на средние для значимых дискриминирующих функций для того, чтобы определить, какие функции и между какими совокупностями проводят дискриминацию.

Дата добавления: 2014-12-26