Сущность и назначение метода

Факторный анализ как метод редукции данных

В случае, когда неизвестный фактор проявляется в изменении нескольких переменных, в процессе анализа можно наблюдать существенную корреляцию или связь между этими переменными. Тем самым факторов может быть существенно меньше, чем измеряемых переменных, число которых, как правило, выбирается исследователем субъективно. Предположим, вы хотите измерить удовлетворенность людей жизнью, для чего составляете вопросник с различными пунктами; среди других вопросов задаете следующие: удовлетворены ли люди своим хобби (пункт 1) и как интенсивно они им занимаются (пункт 2). Результаты преобразуются так, что средние ответы (например, для удовлетворенности) соответствуют значению 100, в то время как ниже и выше средних ответов расположены меньшие и большие значения, соответственно. Две переменные (ответы на два разных пункта) коррелированы между собой. Из высокой коррелированности двух этих переменных можно сделать вывод об избыточности двух пунктов опросника.

Объединение двух переменных в один фактор. Зависимость между переменными можно обнаружить с помощью диаграммы рассеяния. Полученная путем подгонки линия регрессии дает графическое представление зависимости. Если определить новую переменную на основе линии регрессии, изображенной на этой диаграмме, то такая переменная будет включить в себя наиболее существенные черты обеих переменных. Итак, фактически, вы сократили число переменных и заменили две одной. Отметим, что новый фактор (переменная) в действительности является линейной комбинацией двух исходных переменных.

Метод факторного анализа первоначально был разработан именно в психологии с целью выделения отдельных компонент функции интеллекта из многомерных данных по измерению различных проявлений умственных способностей. Основной задачей факторного анализа является нахождение сокращенной системы существенных факторов в пространстве регистрируемых переменных, что включает, как правило, три этапа:

1. выделение первоначальных факторов (выделение главных компонент и выбор компонент, которые отвечают за большую часть дисперсии данных наблюдения

2. вращение выделенных факторов с целью облегчения их интерпретации в терминах исходных переменных

3. содержательная интерпретация новых факторов в предметных терминах, что во многом является творческой задачей исследователя, выходящей за рамки формального метода (отчасти субъективной, но полезной для дальнейшего понимания предмета исследования)

Содержательная интерпретация метода.

Степень влияния фактора на некоторый показатель (переменную) статистически характеризуется величиной дисперсии этого показателя при изменении значений фактора. Если расположить оси исходных переменных ортогонально друг другу (что также является определенным произволом), то можно обнаружить, что в этом многомерном пространстве объекты группируются (своим точечным расположением, определенным координатам точек) в виде некоторого облака или эллипса рассеяния, более вытянутого в одних направлениях и почти плоского в других. Если теперь провести новые оси соответственно осям эллипса рассеяния, то можно говорить о выделении факторов, более субстанциональных, по-сравнению, с исходными переменными, и оценивать сравнительную значимость этих факторов в терминах дисперсии. При этом обычно оказывается, что толщина такого облака рассеяния по некоторым осям настолько мала, что эти оси можно в дальнейшем исключить.

Таким образом, каждый фактор можно представить в виде композиции n-одномерных шкал, заданных на координатных множествах. Фактор, как новая переменная, определяется на основе линии регрессии и включает наиболее существенные черты общих переменных в виде линейной комбинации исходных признаков. Параметр, который объясняет дисперсия фактора (собственного вектора [12] для корреляционной матрицы исходных признаков) носит название собственного значения фактора [13] и определяется решением характеристического уравнения

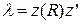
Схема алгоритма вычисления включает следующие шаги:

1. нахождение корреляций r_ij для свойств исходного базиса

2. определение пучков векторов с помощью линейной алгебры

3. определение собственных векторов (обобщающих пучки свойств) и вычисление собственных значений

Формализация метода включает процедуры: нормировки исходных свойств -(X), приведение к единичным векторам -(Y), вычисление матрицы корреляции -(R), нахождение матрицы ортогональных преобразований (факторных весов) - (U) и построение нового ортогонального базиса (ортогональных факторов) –(Z). В зависимости от целей исследования применяют соответствующие методы факторных вращений и расчет индивидуальных факторных весов (новых координат объектов в полученном ортогональном базисе).

Анализ главных компонент. Пример, в котором две коррелированные переменные объединены в один фактор, показывает главную идею факторного анализа или, более точно, анализа главных компонент. Если пример с двумя переменными распространить на большее число переменных, то вычисления становятся сложнее, однако основной принцип представления двух или более зависимых переменных одним фактором остается прежним.

Выделение главных компонент. В основном процедура выделения главных компонент подобна вращению, максимизирующему дисперсию (варимакс) исходного пространства переменных. Например, на диаграмме рассеяния вы можете рассматривать линию регрессии как ось X, повернув ее так, что она совпадает с прямой регрессии. Этот тип вращения называется вращением, максимизирующим дисперсию, так как критерий (цель) вращения заключается в максимизации дисперсии (изменчивости) "новой" переменной (фактора) и минимизации разброса вокруг нее.

Обобщение на случай многих переменных. В том случае, когда имеются более двух переменных, можно считать, что они определяют трехмерное "пространство" точно так же, как две переменные определяют плоскость. Если вы имеете три переменные, то можете построить 3М диаграмму рассеяния.

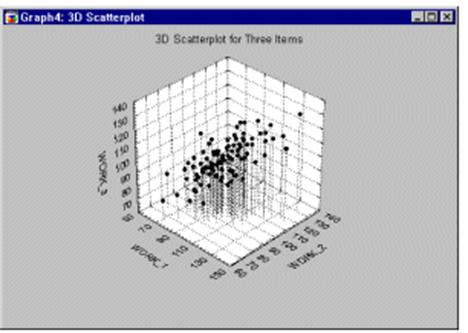
Для случая более трех переменных, становится невозможным представить точки на диаграмме рассеяния, однако логика вращения осей с целью максимизации дисперсии нового фактора остается прежней.

Несколько ортогональных факторов. После того, как найдена линия, для которой дисперсия максимальна, вокруг нее остается некоторый разброс данных, и процедуру повторяют. В анализе главных компонент после того, как первый фактор выделен, то есть, после того, как первая линия проведена, определяется следующая линия, максимизирующая остаточную вариацию (разброс данных вокруг первой прямой), и т.д. Таким образом, факторы последовательно выделяются один за другим. Так как каждый последующий фактор определяется так, чтобы максимизировать изменчивость, оставшуюся от предыдущих, то факторы оказываются независимыми друг от друга. Другими словами, некоррелированными или ортогональными.

Сколько факторов следует выделять. Напомним, что анализ главных компонент является методом сокращения или редукции данных, т.е. методом сокращения числа переменных. Возникает естественный вопрос: сколько факторов следует выделять? Отметим, что в процессе последовательного выделения факторов они включают в себя все меньше и меньше изменчивости. Решение о том, когда следует остановить процедуру выделения факторов, главным образом зависит от точки зрения на то, что считать малой "случайной" изменчивостью. Это решение достаточно произвольно, однако имеются некоторые рекомендации, позволяющие рационально выбрать число факторов.

Обзор результатов анализа главных компонент. Посмотрим теперь на некоторые стандартные результаты анализа главных компонент. При повторных итерациях вы выделяете факторы с все меньшей и меньшей дисперсией. Для простоты изложения считаем, что обычно работа начинается с матрицы, в которой дисперсии всех переменных равны 1.0. Поэтому общая дисперсия равна числу переменных. Например, если вы имеете 10 переменных, каждая из которых имеет дисперсию 1, то наибольшая изменчивость, которая потенциально может быть выделена, равна 10 раз по 1. Предположим, что при изучении степени удовлетворенности жизнью вы включили 10 пунктов для измерения различных аспектов удовлетворенности домашней жизнью и работой. Дисперсия, объясненная последовательными факторами, представлена в следующей таблице:

ФАКТОРНЫЙ АНАЛИЗ	Собственные значения Выделение: Главные компоненты
Значение	Собственные значения	% общей дисперсии	Кумулят. соб. знач.	Кумулят. %
1 2 3 4 5 6 7 8 9 10	6.118369 1.800682.472888.407996.317222.293300.195808.170431.137970.085334	61.18369 18.00682 4.72888 4.07996 3.17222 2.93300 1.95808 1.70431 1.37970.85334	6.11837 7.91905 8.39194 8.79993 9.11716 9.41046 9.60626 9.77670 9.91467 10.00000	61.1837 79.1905 83.9194 87.9993 91.1716 94.1046 96.0626 97.7670 99.1467 100.0000

Дата добавления: 2014-12-26