Зубцовые гармоники ЭДС

Наличие зубцов и пазов на по­верхности статора создает неравно­мерность воздушного

Рис. 7.8 График магнитной индукции основной гармоники В₁,

искаженной зубцовой гармоникой В_z

зазора. По этой причине все гармонические составляющие магнитного поля, обусловленные несинусоидально­стью кривой магнитной индукции (см. рис. 6.2), приобретают зубча­тую форму. Каждая из этих иска­женных гармоник индуцирует в обмотке статора две ЭДС: собст­венной частоты f_v и зубцовую.

Практическое влияние на работу машины может оказать зубцовая ЭДС поля основной

гармоники (рис. 7.8). Мгновенное значение этой ЭДС

e_z = E_zmax sin ω₁ t cos 2Q ω₁ t (7.22)

или, учитывая, что sin ω₁ t cos 2Q ω₁ t = 0,5sin(ω₁ t + 2Q ω₁ t) + 0,5sin(ω₁ t -2Q ω₁ t), получим

e_z = 0,5 E_zmax [sin(2Q+1) ω₁ t – sin (2Q - 1)ω₁ t], (7.23)

где Q = Z₁ /(2p) — число пазов на полюс.

Из (7.23) следует, что зубцовая ЭДС от основной гармони­ки поля может быть разложена на две составляющие с одинаковыми амплитудными значениями, но разными час­тотами:

f_z^/ = (2Q+1)f ₁ (7.24)

f _z^//= (2Q-1)f₁

Рис. 7.9. Скос пазов (а) и скос полюсного наконечника (б)

Например, при 2р = 4, Z₁ = 24 и f₁ = 50 Гц основная гар­моника поля вызывает зубцовые ЭДС, частота которых:

f_z^/ = (2 • 6 + 1)50 = 650 Гц (13-я гармоника);

f'_z^// = (2 • 6 - 1)50 = 550 Гц (11 -я гармоника).

Вредное действие зубцовых гармоник ЭДС выражается в том, что они вызывают дополнительные потери в машине и, имея по­вышенную частоту, оказывают мешающее влияние на линии связи.

Так как сокращение шага обмотки по пазам у₁ всегда кратно числу зубцов, то оно не позволяет уменьшить зубцовые гармоники ЭДС. Эффективное средство ослабления зубцовых гармоник ЭДС - скос пазов или скос полюсных наконечников (в синхронных машинах). Обычно этот скос составляет одно зубцовое деление (рис. 7.9). При скосе пазов или полюсных наконечников ЭДС, ин­дуцируемые в ряде последовательных точек по длине проводника, будут сдвинутыми по фазе относительно друг друга. Это ведет к уменьшению ЭДС проводника, учитываемой коэффициентом ско­са пазов

k_ck =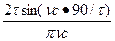

где τ и с — в зубцовых делениях.

При скосе пазов на одно зубцовое деление t₁ для первой гар­моники коэффициент k_CKl ≈ 1, а для гармоник зубцового порядка k_ckv << 1. Например, при 2р = 4, Z₁ = 48 и скосе пазов на одно зуб­цовое деление (с = 1) для основной гармоники (v = 1) коэффициент скоса пазов

k_CKl = 0,995, для зубцовой гармоники (v = 13) коэффициент k_скl3 = 0,590.

Контрольные вопросы

1. Что такое шаг обмотки по пазам и какой должна быть его величина?

2. На какие гармонические составляющие можно разложить несинусоидальную кривую ЭДС,

наведенной в обмотке статора?

3. Какие применяются средства подавления высших гармоник ЭДС в обмотке статора?

4. Каким образом можно ослабить зубцовые гармоники ЭДС в обмотке статора?

ГЛАВА 8

Дата добавления: 2014-12-27