Для этой обмотки эквивалентные параметры будут

q_1экв = q₁c = 1 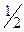• 2 = 3; Z_1экв = Z₁c = 9 • 2 = 18

Изобразив зубцы эквивалентного статора с Z_1экв = 18 (рис. 8.5, а) и разбив их полюсные деления на фазные зоны, пронумеруем пазы реального статора (Z₁ = 9). Эти пазы расположатся между эквивалентными пазами. Из разметки пазов видно, что каждая фазная обмотка состоит

из двух катушечных групп, при этом одна группа состоит из двух катушек, а другая — из одной. Изобразив кату­шечные группы фазы А (рис. 8.5, б), соединяем их последователь­но (встречно) и обозначаем выводы этой фазной обмотки С1 и С4. Аналогично выполняем схемы фазных обмоток фаз В и С.

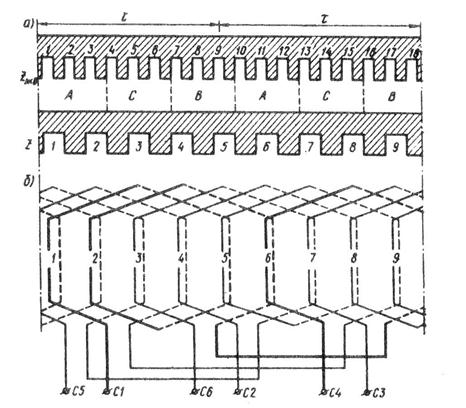
Рис. 8.5. Трехфазная обмотка статора с дробным q₁

В рассмотренном примере в обмотке с q₁ =1 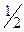каждая катушечная группа состоит из двух не равных по числу катушек частей: в одной части катушечной группы — одна катушка, а в другой — две катушки. Таким образом, в каждой катушечной группе имеет место чередование катушек, обозначаемое 1 — 2. Если дроб­ей часть q₁ отличается от 1/2, то чередование катушек в каждой катушечной группе будет другим [10].

Чередование катушек в катушечной группе подчиняется следующему правилу: количество цифр чередования равно знаменателю неправильной дроби с [см. (8.1)], а сумма этих цифр равна числителю неправильной дроби ас + b.

Дата добавления: 2014-12-27