Высшие пространственные гармоники магнитодвижущей силы трехфазной обмотки

Полюсное деление МДС высших пространственных гармоник обратно пропорционально номеру гармоники: τ_v = τ /v. Поэтому пространственная периодичность этих гармоник растет пропорционально номеру гармоники (см. рис. 9.1). Учитывая изложенное, запишем уравнение МДС третьей гармоники фазных обмоток:

f_3A = F_3A sin ω₁t cos3α;

f_3B = F_3B sin(ω₁t – 120 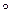)cos3(α – 120 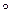) = F_3A sin (ω₁t –120 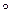)cos3α;

f_3C = F_3C sin(ω₁t– 240 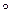)cos3α (α – 240 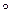) = F_3A sin (ω₁t – 240 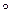) cos3α.

откуда МДС третьей гармоники трехфазной обмотки

f₃ = f_3A + f_3B + f_3C = 0, (9-17)

т. е. результирующая МДС третьей гармоники в трехфазной об­мотке статора при симметричной нагрузке фаз равна нулю. Это распространяется также и на высшие гармоники, кратные трем (9, 15 и др.). МДС высших гармоник оставшихся номеров (5, 7 и др.) ослабляются распределением обмотки в пазах, укорочением шага катушек и скосом пазов.

МДС высших гармоник многофазной обмотки статора - вращающиеся. При этом частота их вращения n_v в раз меньше частоты вращения МДС основной гармоники:

n_v = n₁/ . (9.18)

Направление вращения этих МДС зависит от номера гармоники: МДС гармоник порядка 6х + 1 вращаются согласно с МДС основной гармоники — прямовращающиеся МДС, а МДС порядка 6х - 1 вра­щаются встречно МДС основной гармоники — обратновращающиесяМДС (здесь х= 1, 2, 3,...).

Вращающиеся магнитные поля, созданные высшими гармони­ческими составляющими МДС, индуцируют в обмотке статора ЭДС основной частоты). Действительно, частота ЭДС, наведен­ной магнитным полем любой пространственной гармоники,

f_v = n_v p_v/ 60 = n₁ pv/ ( 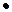60) = f₁ (9.19)

где p_v = p ; n_v = n₁/ .

Контрольные вопросы

1. Почему гармонические составляющие МДС обмотки статора называют про­странственными?

2. Какие методы подавления высших пространственных гармоник применяют и машинах переменного тока?

3. Какова зависимость частоты вращения МДС обмотки статора от частоты то ка и числа полюсов в обмотке статора?

4. Как изменить направление вращения МДС обмотки статора?

5. Каково относительное значение магнитной индукции обратной составляю щей поля статора при круговом, эллиптическом и пульсирующем магнитных полях?

Дата добавления: 2014-12-27