Основные операции с данными и их характеристики

Данные – диалектическая составная часть информации. Они представляют собой зарегистрированные сигналы. В соответствии с методом регистрации данные могут храниться и транспортиро­ваться на носителях различных видов. Самым распространенным носителем дан­ных является бумага. На бумаге дан­ные регистрируются путем изменения оптических характеристик ее поверхности.

Любой носитель можно характеризовать параметром разрешающей способности (количеством данных, записанных в принятой для носителя единице измерения) и динамическим диапазоном (отношением амплитуд максимального и минимального регистрируемых сигналов). От этих свойств носителя нередко зависят такие свойства информации, как полнота, доступность и достоверность. Обработка и преобразование данных различных форматов являются важнейшими задачами, как общей информатики, так и её прикладных ветвей.

Обработка данных включает в себя множество различных операций (рис. 1.11). Приведенный список операций с данными не является исчерпывающим. Важно другое: работа с информацией может иметь огромную трудоемкость, что и определяет актуальность задачи автоматизации приведенных операций.

С развитием средств связи и вычислительной техники и их использованием для передачи и обработки инфор­мации возникла необходимость найти методы измерения количественных характеристик информации.

В настоящее время для измерения количества информации существуют два подхода.

Первый подход основан на определении «физического объема» информации:

— Физический объем информации – это длина представляемого текста.

— Информационная емкость – количество передаваемой информации.

— Компактность – со­отношение информационного и физического объемов.

— Информационная плотность – соотношение информа­ционной емкости и информационного объема.

Единицами измерения объемов нормативного текста могут быть: количество статей в нормативно – правовом акте, число типографских страниц, которые занимает изучаемый нормативный акт, число фраз, содержащихся в данном акте, и т. д.

Второй подход основан на положениях теории ин­формации, разработанной американским ученым К. Шенноном. Здесь фундаментальное значение имеют два понятия: неопределенность и энтропия.

Неопределенность – это отсутствие информации о системе и ее состояниях. Следовательно, понятия информации и неопределенности тесно связаны и дополняют друг друга. Чем более увеличивается знание об исследуемом событии или явлении, тем меньше становится неопределенность.

Информация в сообщении приобретает смысл только тогда, когда состояние исследуемой системы «случайно» (неопределен­но, неизвестно). Полученные сведения о событиях или явлениях тем ценнее и содержательнее, чем больше была неопределенность о них до получения этих сведений.

Энтропия – это количественная мера неопределен­ности. При получении сведений об объекте мера неопределенности уменьшается. Величина, на которую уменьшилась энтропия, и есть количество полученной информации.

Для рассмотрения формулы К. Шеннона примем следующие обозначения:

Н₀ (х) – энтропия случайной величины до получения сообщения;

Н₁ (х) – энтропия случайной величины после получения сообщения о ее состоянии (остаточная энтропия);

Н (х) – разность величин Н₁ (х) и Н₀ (х).

Тогда количество информации может быть представлено в следу­ющем виде:

Н (х) = Н₀ (х) – Н₁ (х).

К. Шеннон предложил знаменитую формулу для измерения энтропии

Н(х) = – 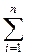Р_{i *} log Р_i, (1.1)

где: Н (х) – символ энтропии;

х – исследуемое случайное событие (явление);

Р_i – вероятность реализации i – го элемента сложного явления (i = 1… n);

п – число состояний системы;

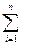– знак суммы;

1оg Р_i – логарифм вероятности отдельно взятого элементарного события.

В данной формуле логарифм (показатель степени, в которую нужно возвести некото­рое число - основание, чтобы получить данное) используется с целью удобства при выполнении математических действий (сложения, вычитания и др.) над различными величина­ми, получаемыми в результате измерения информации.

Рассчитываемая таким образом мера неопределенности случайного события может принимать значения от 0 до 1 включительно.

Формула К. Шеннона позволяет ввести единицу информации. За единицу информации принято считать такое количество информации, которое содержится в исходе опыта (сообщения), когда за возможные принимаются только два состояния (1 или 0). При этом каждое состояние может быть реализовано с одинаковой вероятностью.

Приведем элементарный расчет.

Условия:

Р₁ = Р₂ = 0,5; n = 2.

Подставляем эти данные в формулу Шеннона, получаем:

H(х) = – [0,5 ×log 1/2 + 0,5 ×log 1/2]= – [0,5×(– 1) + 0,5×(– 1)] = 1.

Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита.

Для радиоэлектронных элементов (радиоламп, полупроводниковых элементов, конденсаторов), которые в основном использовались и используются в вычислительных машинах, характерно наличие двух устойчивых состояний. Например, электронная лам­па может быть «открыта» (тогда через нее идет ток) или «заперта» (ток через нее не проходит). По тому же принципу «да» или «нет» работают и полупроводнико­вые элементы, которые сейчас уже полностью вытес­нили радиолампы из вычислительной техники. Эти свой­ства радиоэлектронных элементов и служат основной причиной применения в вычислительной технике двоичной системы счисления.

В двоичной системы счисления числа записываются с помощью двух цифр 0 и 1 и называются двоичными. Система перевода данных в двоичные числа называется двоичным кодированием. Битом называется такое количество информации, которое можно представить одноразрядным двоичным числом (0 или 1).

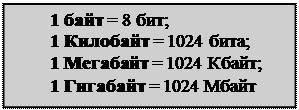Часто используются и другие, более крупные единицы измерения информации, например:

В компьютере один знак текста требует объем памяти, равный одному байту. Стандартный лист формата А4 содержит примерно 3200 знаков размера 12 пунктов. Это примерно 3 Кб. Таким образом, на жестком диске компьютера объемом 20 гигабайт может храниться примерно 60 – 70 миллионов таких страниц.

Одной из важнейших операций, проводимых с данными, является их транспортировка. В большинстве случаев транспортировка производится по каналам связи, которые создавались для передачи аналоговых электрических сигналов (речевых сообщений). Цифровая информация также передается по этим каналам, но она предварительно преобразуется в аналоговый сигнал с помощью различных видов модуляции. Виды сигналов в каналах связи и с выхода компьютера представлены на рисунке 1.12, где по горизонтальной оси отложено время, по вертикальной – амплитуда сигналов.

Для измерения скорости передачи цифровых данных применяется единица измерения бит/сек (количество передаваемых бит в секунду). В среднем, при передаче данных каждым десяти символам соответствует один символ машинописного текста. Часто скорость передачи данных измеряют в символах в секунду (обозначается CPS – от английского Character Per Second).

Дата добавления: 2014-12-27