Методика введения понятия алгоритма

Кц

Все

Кц

Здесь использован цикл с предусловием — основной тип циклической команды (нц — начало цикла, кц — конец цикла). Рассмотрим еще один пример: Робот движется вдоль горизонтальной стены и закрашивает только пустые (не закрашенные) клетки.

нц пока снизу стена

если клетка не закрашена

то закрасить

вправо

Авторы учебника [14] интерпретируют своего исполнителя следующим образом: Робот — это автоматическое устройство, управляемое компьютером. Между компьютером и Роботом имеется прямая и обратная связь. По прямой связи от ЭВМ к Роботу передаются управляющие команды, по обратной связи — ответы Робота на запросы о текущей обстановке. Например, фраза «снизу стена» обозначает запрос компьютера к Роботу на проверку условия: находится ли под ним стена. В результате Робот по обратной связи отвечает «да» или «нет» в зависимости от обстановки. То же самое относится к фразе «клетка не закрашена».

Из рассмотренных примеров следует вывод о том, что лишь при наличии обратной связи алгоритмы управления исполнителем могут иметь сложную структуру, содержащую циклы и ветвления. Без обратной связи алгоритмы могут быть только линейными.

На примере исполнителя Робота вводится понятие вспомогательного алгоритма и метода последовательного уточнения (нисходящего проектирования; программирования сверху вниз). Пример использования Робота в учебнике [14] доказывает, что ограничиваясь исполнителями и алгоритмами, работающими без величин, можно успешно обучать структурной методике программирования.

В язык Робота постепенно включается использование величин со всеми их атрибутами: именем, значением, типом. Все команды Чертежника, кроме «поднять перо», «.опустить перо», используют параметры, которые являются величинами.

Языком описания алгоритмов для всех исполнителей является учебный алгоритмический язык (АЯ). За основу взята версия АЯ, описанная в учебнике А.П.Ершова [15]. Однако введены некоторые модификации в изобразительные средства языка. Введение в учебнике [14] всякой новой конструкции алгоритмического языка происходит по одинаковой методической схеме:

• рассматривается новая задача, требующая введения новой конструкции;

• описывается алгоритм решения этой задачи;

• дается формальное описание данной конструкции в общем виде.

Наряду с алгоритмами для Робота и Чертежника в учебнике [14] рассматриваются алгоритмы вычислительного характера, ориентированные на универсального исполнителя обработки информации — компьютер. Это типовые задачи обработки числовой и символьной информации: вычисление числовых последовательностей, обработка массивов, литерных строк и пр. Рассматриваются также алгоритмы решения содержательных задач методами математического моделирования.

В целом можно сказать, что в учебнике [14] алгоритмическая линия школьной информатики проработана наиболее полно и последовательно как в содержательном, так и в методическом плане.

Алгоритмическая линия в учебнике Л!Г. Гейна [12] реализована по двум направлениям. Первое направление заключается в использовании учебных исполнителей алгоритмов, работающих «в обстановке», подобно тому, как это делается в учебнике [14]. Второе направление заключается в обучении построению вычислительных алгоритмов для решения задач математического моделирования.

В учебнике [12] также применен исполнитель с названием «Чертежник», который относится к категории исполнителей, работающих по принципу «черепашьей графики». В отличие от Чертежника из учебника А. Г. Кушниренко, его команды перемещения (сделать шаг, прыгнуть) и вращения (повернуть налево) не имеют параметров. По одной команде исполнитель перемещается на строго определенное расстояние — один шаг, или поворачивается против часовой стрелки на 90°. Поэтому создаваемые рисунки могут состоять только из горизонтальных и вертикальных отрезков. В этом смысле изобразительные возможности данного исполнителя более скромные, чем у Чертежника А. Г. Кушниренко. Можно сказать, что Чертежник А. Г. Гейна в чистом виде является исполнителем, работающим «в обстановке».

Для моделирования методов решения задач обработки табличной информации в [12] введен исполнитель Робот-манипулятор. Прямоугольная таблица имитируется стеллажом, состоящим из ячеек, в которые могут быть помещены различные радиодетали (микросхемы, транзисторы и пр.). Робот умеет перемещаться в вертикальном и горизонтальном направлениях вдоль ячеек, помещать в них детали или извлекать детали из ячеек. Здесь можно говорить о появлении величин, рассматривая имя детали в ячейке как величину (производится сравнение ее имени с именем искомой детали). Характерная структура алгоритмов управления Роботом — вложенные циклы с ветвлениями.

Второе направление алгоритмической линии в учебнике [12] — алгоритмы решения вычислительных задач. Для построения таких алгоритмов используется учебный исполнитель Вычислитель. Это исполнитель, работающий только с числовыми величинами. Поскольку в качестве языка программирования для реализации вычислительных алгоритмов на ЭВМ используется Бейсик, то и язык Вычислителя «бейсикообразен». Несмотря на неструктурный характер используемой версии Бейсика, авторы стараются оставаться в рамках структурного подхода. В частности, это проявляется в том, что в языке Вычислителя отсутствует команда перехода.

Для моделирования понятия переменной применительно к Вычислителю используется образ ящика. Имя переменной — это буква, записанная на «ящике», а присваиваемое ей значение — это величина (число), помещаемое в «ящик». Составление программы на Бейсике по данному алгоритму интерпретируется как перевод с языка Вычислителя на язык Бейсик. При этом «ящики» для переменных заменяются на ячейки памяти ЭВМ, а при записи программы требуется строго соблюдать правила синтаксиса Бейсика. Для программирования цикла с предусловием в учебнике предлагается использовать стандартный способ его реализации с помощью операторов IF GOTO (для версий Бейсика, в которых нет оператора WHILE).

В учебнике В.А.Каймина и др. [13] не применяется методика учебных исполнителей. Изучение алгоритмизации ориентируется на исполнителя-ЭВМ. Для описания алгоритмов используется алгоритмический язык, близкий к варианту А.П.Ершова. Блок-схемы практически не используются. В учебнике [13] рассматриваются вычислительные задачи, а также задачи на построение графических изображений. Языком реализации алгоритмов на ЭВМ является Бейсик. Как и в учебнике [12], авторы уделяют внимание стандартным приемам программирования на неструктурном Бейсике циклов и ветвлений.

В учебнике третьего поколения А. Г. Гейна и др. [2] существенно изменился подход к обучению алгоритмизации и программированию по сравнению с учебником [12] того же авторского коллектива. Введен новый учебный исполнитель Паркетчик. Для того, чтобы подчеркнуть формальный характер работы исполнителей алгоритмов, авторы используют термин «Бездумные исполнители» — БИ. Таким образом, Паркетчик представляет из себя БИ, назначение которого — выкладывать на клетчатом поле узоры из разноцветных плиток (красных и зеленых). Поле имеет прямоугольную форму; каждая клетка идентифицируется двумя индексными номерами — по горизонтали и по вертикали, например: (1,1), (3,5) и т.п.

Паркетчик может перемещаться с помощью команд «шаг вверх», «шаг вниз», «шаг влево», «шаг вправо» к соседним клеткам, а также к любой клетке поля по команде «перейти на (т, п)». В текущую клетку Паркетчик может положить плитку указанного цвета по команде «положить (цвет)» или убрать плитку по команде «снять плитку». Условиями в командах ветвления и цикла может быть проверка цвета лежащей плитки или проверка наличия препятствия (стены) в любом направлении от текущей клетки.

Паркетчик предназначен для методичного обучения структурному способу построения алгоритмов. Форма языка Паркетчика применяется также и для описания вычислительных алгоритмов, подобно тому, как используется алгоритмический язык в учебнике А.Г.Кушниренко [14]. По сути дела, между алгоритмическим языком и языком Паркетчика нет принципиальной разницы. И тот и другой представляет собой структурный русскоязычной псевдокод. Видимо, считая описание алгоритма на языке Паркетчика достаточно структурированным и наглядным, авторы отказались от использования в учебнике [2] блок-схем.

В учебнике [2] предлагаются для изучения два языка программирования: QBasic и Паскаль. Поскольку QBasic является структурированной версией Бейсика, то нет принципиальной разницы в выборе того или другого языка для начального обучения программированию.

В учебнике А. А. Кузнецова и Н.В.Агапьевой [8] каких-то специальных учебных средств для описания алгоритмов не используется. Значительный по объему раздел «Введение в программирование» ориентирован на начальное изучения Паскаля на примерах задач вычислительного характера, а также задач построения графических изображений и обработки строк.

В учебнике И.Г.Семакина и др. [6] применен отличный от рассмотренных подход к теме алгоритмизации. Его можно назвать кибернетическим подходом. Алгоритм трактуется как информационный компонент системы управления. Такой подход дает возможность ввести в содержание базового курса новую содержательную линию — линию управления. Это многоплановая линия, которая позволяет затронуть следующие вопросы:

• элементы теоретической кибернетики: кибернетическая модель управления с обратной связью;

• элементы прикладной кибернетики: структура компьютерных систем автоматического управления (систем с программным управлением); назначение автоматизированных систем управления;

• основы теории алгоритмов.

Для того чтобы соблюсти принцип инвариантности содержания по отношению к конкретным версиям программного обеспечения, в учебнике [6] описывается гипотетический учебный исполнитель, которому дано имя ГРИС — графический исполнитель. Это исполнитель, работающий «в обстановке» (т.е. без использования величин). Наиболее близкими к нему являются Кенгуренок (пакет учебного ПО фирмы КУДИЦ) и Чертежник (учебник А. Г. Гейна [2]). На примере ГРИС вводятся основные понятия алгоритмизации. Предлагаемая последовательность заданий способствует эффективному достижению основной цели раздела — освоения структурной методики построения алгоритмов.

Изучаемые вопросы:

ª Определение алгоритма.

ª Свойства алгоритма.

ª Типы алгоритмических задач.

Определение и свойства алгоритма. В учебника [6] дано следующее определение алгоритма: «Алгоритм — понятное и точное предписание исполнителю выполнить конечную последовательность команд, приводящих от исходных данных к искомому результату».

В этом определении содержатся основные понятия, связанные с алгоритмом и его главные свойства. Взаимосвязь понятий отражена на рис 11.1.

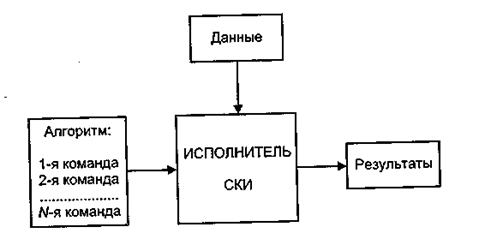
Рис. 11.1. Схема функционирования исполнителя алгоритмов

Центральным объектом в этой системе является ИСПОЛНИТЕЛЬ алгоритмов. Исполнитель — это тот объект (или субъект), для управления которым составляется алгоритм. Основной характеристикой исполнителя, с точки зрения управления, является система команд исполнителя (СКИ). Это конечное множество команд, которые понимает исполнитель, т.е. умеет их выполнять.

Для выполнения всякой работы, решения поставленной задачи исполнитель на входе получает алгоритм и исходные данные, а на выходе получаются требуемые результаты. Алгоритм может включать в себя только команды, входящие в СКИ. Это требование к алгоритму называется свойством понятности.

Другое свойство алгоритма — точность. Всякая команда должна быть сформулирована так, чтобы определить однозначное действие исполнителя. Например, кулинарный рецепт можно рассматривать как алгоритм для исполнителя-повара по приготовлению блюда. Но если одним из пунктов в нем будет написано: «Положить несколько ложек сахара», то это пример неточной команды. Сколько ложек? каких ложек (чайных, столовых)? Каждый повар может это понимать по-своему, и результаты будут разными. Пример точной команды: «Положить 2 столовые ложки сахара».

Работа исполнителя состоит в последовательном формальном выполнении команд алгоритма. Отсюда следует вывод о возможности создания автоматических исполнителей. В частности, таким автоматическим исполнителем алгоритмов по обработке информации является компьютер.

Еще одно свойство, которое отражено в определении алгоритма — конечность. Оно формулируется так: исполнение алгоритма и, следовательно, получение искомого результата должно завершиться за конечное число шагов. Здесь под шагом подразумевается выполнение отдельной команды. Это свойство является предупреждением ситуации, которую программисты называют зацикливанием. Бесконечно исполняемый алгоритм безрезультатен. Поэтому свойство конечности называют еще результативностью алгоритма.

В учебной литературе встречается описание еще двух свойств алгоритмов: дискретности и массовости. «Дискретность состоит в том, что команды алгоритма выполняются последовательно, с точной фиксацией моментов окончания выполнения одной команды и начала выполнения следующей» [20]. Однако (с нашей точки зрения) это свойство можно не выделять, поскольку требование последовательного выполнения команд заложено в определении алгоритма.

«Свойство массовости выражается в том, что алгоритм единым образом применяется к любой конкретной формулировке задачи, для решения которой он разработан» [20]. Другими словами, это можно назвать универсальностью алгоритма по отношению к исходным данным решаемой задачи. Заметим, что данное свойство не является необходимым свойством алгоритма, а скорее определяет качество алгоритма: универсальный алгоритм лучше неуниверсального (алгоритм решения частной задачи — тоже алгоритм!).

Основные типы учебных алгоритмических задач. Для закрепления основных понятий, связанных с определением алгоритма, полезно рассмотреть с учениками несколько заданий следующего содержания:

1) выполнить роль исполнителя: дан алгоритм, формально исполнить его;

2) определить исполнителя и систему команд для данного вида работы;

3) в рамках данной системы команд построить алгоритм;

4) определить необходимый набор исходных данных для решения задачи.

В качестве примера задачи первого типа можно использовать алгоритм игры Ваше, рассматриваемый в учебниках [6, 8, 15]. В книгах [8, 15] правила игры определены так: в игре используются 7, 11, 15, 19 предметов. За один ход можно брать 1, 2 или 3 предмета. Проигрывает тот игрок, который берет последний предмет. Предлагается алгоритм выигрыша для первого игрока. В книге [6] правила несколько другие. В игре используются 11, 16, 21, 26,... предметов. За один ход можно брать от 1 до 4 предметов. Рассматривается алгоритм, благодаря которому всегда выигрывает игрок, берущий вторым.

После того как ученики поиграли в эту игру по тем правилам, что описаны в учебнике, можно предложить им несколько заданий аналитического характера на тему игры Ваше. Задания могут быть предложены в качестве домашней работы.

Задача 1. «Разгадать загадку» алгоритма, т.е. объяснить, почему второй игрок всегда выигрывает (для варианта [6])?

Решение. По данным правилам второй игрок будет всегда выигрывать, если общее число камней определяется формулой: N = 5k + 1. Здесь k — любое натуральное число.

Задача 2. Составить алгоритм, по которому игрок, делающий первый ход, может выиграть в том случае, если соперник не знает выигрышной тактики.

Решение. Необходимо перехватить инициативу, т. е. оказаться в положении второго игрока, который дополняет предыдущий ход соперника до 5 камней. Это возможно лишь в случае ошибки соперника. Начать игру можно так:

1. Взять 1 камень.

2. Предоставить ход сопернику; соперник взял п камней.

3. Если п + 1 < 5, то взять 5 — (п + 1) камней.

4. Предоставить ход сопернику.

И далее играть по выигрышному алгоритму для второго игрока.

Следующая задача требует от учеников незаурядных математических навыков.

Задача 3. Попробуйте провести математический анализ игры Баше в общем случае для N камней. Определите правила игры (т. е. сколько камней можно брать за один ход), при котором имеется выигрышный алгоритм. Опишите этот алгоритм в виде последовательности команд.

Решение. Выигрышный алгоритм для второго игрока можно построить только в тех случаях, когда исходное число камней (N) представимо в виде: N = Х´К+ 1, где X и К— натуральные числа. По правилам игры за один ход можно брать от 1 до X— 1 камней. Второй игрок будет всегда выигрывать, если своим ходом он будет дополнять число камней, взятых соперником, до X. Например, пусть N = 25. Это значение можно представить: 25 = 4´6 + 1. Следовательно, правило игры должно быть таким: за один ход можно брать 1— 2— 3 камня. А для того, чтобы второй игрок всегда выигрывал, в свой ход он должен дополнять ход соперника до 4 камней.

Следующая задача относится ко второму типу из приведенной выше классификации.

Задача 4. Назвать исполнителя следующего вида работы — выдача заработной платы; определить СКИ исполнителя.

Решение. Очевидно, исполнителя можно назвать «Кассир». Система команд, которые он должен уметь выполнять, следующая:

— найти в ведомости получателя;

— посчитать деньги;

— выдать деньги.

В задачах такого типа нужно учить учеников разбивать работу исполнителя на сравнительно простые действия, которые требуют формального исполнения. Команда «выдать зарплату» не удовлетворяет таким требованиям.

При построении СКИ решаются две проблемы: проблема элементарности команд и проблема полноты системы команд. Система команд исполнителя называется полной, если она содержит весь минимально-необходимый набор команд, позволяющий построить любой алгоритм в том классе задач, на который ориентирован исполнитель.

Рассмотрим еще один пример задания второго типа.

Задача 5. Описать систему команд исполнителя «Геометр», который мог бы выполнять геометрические построения с помощью циркуля и линейки.

Решение. Ученикам знаком класс задач, которые в геометрии называются задачами на построение с помощью линейки, циркуля и карандаша. Полной системой команд для исполнителя «Геометр» является следующий список:

1. Провести отрезок прямой между двумя данными точками.

2. Установить раствор циркуля, равный длине данного отрезка.

3. Установить ножку циркуля в данную точку.

4. Провести окружность.

5. Выделить общие точки двух линий (пересечения или касания). Обратите внимание на элементарность каждой команды. Делить их на более простые не имеет смысла.

Следующая задача относится к третьему типу.

Задача 6. Записать для Геометра алгоритм решения следующей задачи: дан отрезок АВ; построить окружность, для которой отрезок АВ является диаметром.

Решение.

Алгоритм ОКРУЖНОСТЬ ДАННОГО ДИАМЕТРА

Дата добавления: 2014-12-27