Примеры решения задач. Рис. 11.8. Исполнение компьютером вычислительного алгоритма

Кон

Нач

ввод А

ввод В

С:= А + В

вывод С

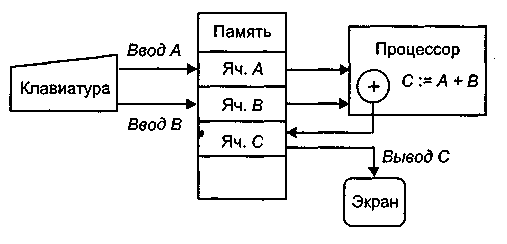
Рис. 11.8. Исполнение компьютером вычислительного алгоритма

Эффективным методическим средством, позволяющим достичь понимания программирования, является ручная трассировка алгоритмов, которая производится путем заполнения трассировочной таблицы.

Рассмотрим несколько задач, назначение которых состоит в закреплении понятий «переменная», «присваивание». Условия задач взяты из списка заданий к подразделу 12.1 учебника [6].

Пример 1. Вместо многоточия впишите в алгоритм несколько команд присваивания, в результате чего получится алгоритм возведения в 4-ю степень введенного числа (дополнительных переменных кроме А не использовать):

ввод А... вывод А

Решение. Ввод А

А:= А*А (А²)

А:= А*А (A⁴)

Вывод А

Пример 2. Написать на АЯ алгоритм вычисления У по формуле:

Y= (1 — X² + 5Х⁴)²,

где X— данное целое число. Учесть следующие ограничения: 1) в арифметических выражениях можно использовать только операции сложения, вычитания и умножения; 2) выражение может содержать только одну арифметическую операцию. Выполнить трассировку алгоритма при X = 2.

Решение. Ученики могут построить разные варианты алгоритма решения этой задачи. Для сохранения промежуточных результатов можно использовать дополнительные переменные. Обсуждая эту задачу, полезно рассмотреть вариант алгоритма, при котором не понадобится дополнительных переменных, т. е. можно обойтись всего двумя переменными Хи Y. Тем самым достигается экономия памяти компьютера. Вот как выглядит этот алгоритм и его трассировка (табл. 11.2):

Таблица 11.2

Команда	X	Y
Ввод X	2
X = X * X
Y = 1 - X		-3
X = X * X
X = 5 * X
Y = Y + X
у = у * Y
Вывод У

Пример 3. Пользуясь ограничениями предыдущей задачи, написать наиболее короткие алгоритмы вычисления:

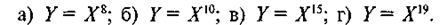
Постараться использовать минимальное количество дополнительных переменных. Выполнить трассировку алгоритмов.

Решение. Выполним вариант г) задания. Построим алгоритм, учитывая равенство: X¹⁹ = Х¹⁶-Х*. Значения X^k, где k = 2", быстро вычисляются л-кратным умножением переменной самой на себя. Алгоритм:

Ввод X

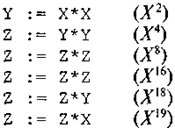
Вывод Z

Пример 4. Записать алгоритм циклического обмена значениями трех переменных А, В, С. Схема циклического обмена:

Например, если до обмена было: А = 1, В = 2, С = 3, то после обмена должно стать: А = 3, В= I, С = 2. Выполнить трассировку.

Решение. Эта задача является естественным продолжением задачи об обмене значениями двух переменных, рассмотренной в [6]. Идея прежняя: для обмена значениями требуется дополнительная переменная, обозначим ее — X. Вот как будет выглядеть алгоритм и его трассировка:

Таблица 11.3

Команда	А	B	С	X
Ввод А, В, С		2
Х:=С
С:=В
В:=А
А:=Х
ВыводА, В, С

Дата добавления: 2014-12-27