Определитель Грама

П р а в и л о в ы р о ж д е н н о с т и С и л ь в е с т р а

В ы р о ж д е н н о с т ь

Особенная матрица

Линейная независимость векторов

Векторы x_i (i=1, 2, 3, …, m) называются линейно независимыми, если не существует постоянных величин k_i (i=1, 2, 3,…, m), из которых хотя бы одна отлична от нуля, так что можно было бы записать:

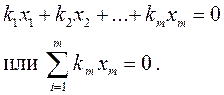
Если строки или столбцы матрицы не являются линейно-независимыми, в этом случае определитель этой матрицы равен нулю.

Если строки особенной матрицы связаны одним линейным соотношением, то матрица называется просто вырожденной или однократно вырожденной. Если строки особенной матрицы связаны более чем одним линейным соотношением, то матрица многократно вырожденная.
Рангом r матрицы А называется наивысший порядок миноров матрицы А, отличных от нуля.

r = n – q,

где q – вырожденность, или дефект.

Дефект произведения матриц не меньше дефектов каждой из матриц и не больше суммы дефектов матриц-сомножителей:

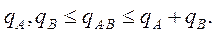
Определитель Грамастроится для системы векторов в предположении, что векторы x_i линейно зависимы:

.

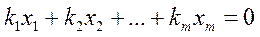Запишем последовательно скалярные произведения векторов x_i :

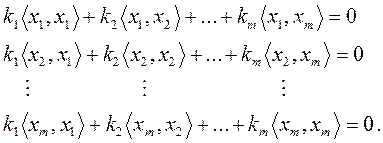
Известно, что система однородных уравнений (в данном случае относительно неизвестных k_i) имеет нетривиальное решение только в том случае, если определитель матрицы с коэффициентами < x_i , x_j > равен нулю. Этот определитель и называется определителем Грама:

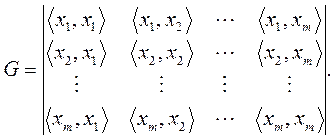
В результате можно сделать следующий вывод.

Системавекторов x₁,…, x_m линейно независима в том случае, когдаопределитель Грама не равен нулю.

В том случае, когда x₁,…, x_m – система ортогональных векторов, определитель Грамаприобретает диагональный вид.

Вопросы к разделу 2.5

1. В чем состоит условие ортогональности векторов?
2. Результатом скалярного произведения двух векторов является скаляр, а результатом векторного произведения?
3. Почему неравенство 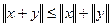называется неравенством треугольника?
4. Почему в неравенстве Шварца 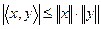в левой части используются одинарные прямые вертикальные скобки, а в правой – двойные?
5. Что называется дефектом особенной матрицы?
6. Что такое ранг матрицы?
7. Какие векторы являются линейно независимыми?
8. Что можно сказать о системе векторов, для которой определитель Грама равен нулю?
9. Что можно сказать о системе векторов, для которой определитель Грама имеет диагональный вид?

Дата добавления: 2014-12-27