Модальная матрица

Формула Бохера

Можно записать полезную рекуррентную формулу, выражающую коэффициенты характеристического уравнения через следы матриц различного порядка T_k = Tr(A^k):

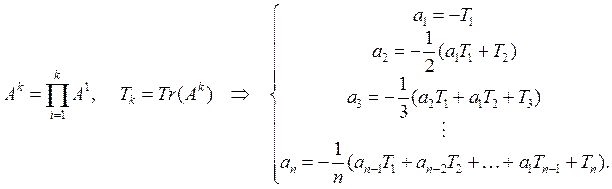
Эта формула, известная как формула Бохера, эффективна при вычислении коэффициентов характеристического уравнения с помощью компьютерной программы.

Пример. Найти характеристические числа следующей заданной матрицы А:

.

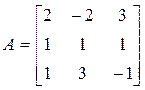По формуле Бохера: a₁ = – T₁= – ( 2 + 1 – 1 )= – 2. Произведение матрицы А на себя:

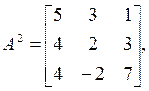
откуда

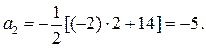
Аналогично

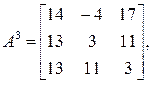
откуда

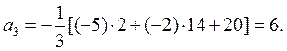
Следовательно, характеристическое уравнение имеет вид:

λ +2 λ –5 λ =(λ –1)(λ +2)(λ –3)=0.

Найдем характеристические числа: λ₁ = 1, λ₂ = – 2, λ₃ = 3.

Для каждого из n характеристических чисел λ_i (i=1,2,…,n) матрицы А (в предположении, что все они различны) можно получить решение уравнения [ λ E – A ] x = 0. Это векторно-матричное уравнение можно представить в виде системы уравнений

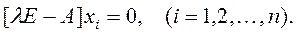
Векторы x _i, представляющие собой решения данной системы уравнений, являются характеристическими векторами матрицы A. Поскольку эта система уравнений однородная, то и k_ix_i, где k_i – произвольная скалярная величина, также служит решением. Поэтому эта система уравнений определяет однозначно только направление каждого из x _i.

Матрица, образованная векторами-столбцами k_ix_i, называется модальной матрицей. (Модальная – от слова “ mode ”, означающего «частота». Так называемые «частоты», описывающие динамику линейной системы, могут быть выражены в виде составляющих движения вдоль характеристических векторов).

При различных характеристических числах столбцы модальной матрицы могут выбираться равными или пропорциональными произвольному столбцу присоединенной матрицы Adj [ λ E – A ].

Это вытекает из того факта, что [ λ E – A ] имеет ранг n – 1. Поскольку определитель | λ E – A |= 0 (как мы уже выяснили), ранг матрицы Adj [ λ E – A ] должен быть меньше n, однако при этом он не может быть меньше n – 1, так как тогда равнялись бы нулю все (n – 1) миноров строки определителя | λ E – A |, что, в свою очередь, потребовало бы, чтобы

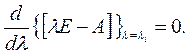
Отсюда следует, что λ_i является кратным корнем исходной системы уравнений, а это противоречит предположению о том, что характеристические числа различны. Таким образом, матрица [ λ E – A ] имеет ранг (n – 1 ), поэтому из определения присоединенной матрицы следует, что столбцы модальной матрицы пропорциональны произвольному ненулевому столбцу Adj [ λ E – A ]. Ввиду линейной зависимости столбцов Adj [ λ E – A ] для данного λ_i выбор каждого λ_i определяет только один столбец модальной матрицы.

Пример. Найти характеристические числа и модальную матрицу, соответствующую матрице А:

.

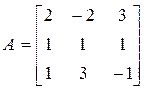Характеристическое уравнение находим из условия | λ E – A |=0:

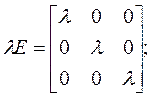
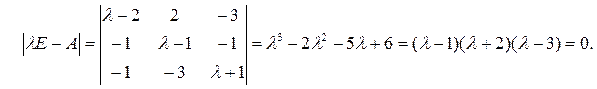
Характеристические числа: λ₁ = 1, λ₂ = – 2, λ₃ = 3.

Присоединенная матрицаравна:

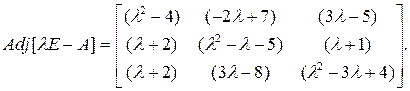
Чтобы найти модальную матрицу, необходимо в присоединенную матрицу подставить значение собственных (характеристических) чисел.

При λ₁ = 1присоединенная матрица равна

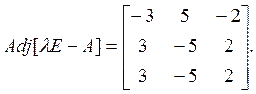
При λ₂ = – 2присоединенная матрица равна

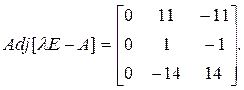
При λ₃ = 3присоединенная матрица равна

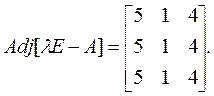
Поскольку характеристические векторы единственным образом определяют только направление, то умноженные на скалярную величину, они также будут удовлетворять уравнению

.

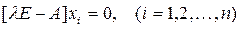Следовательно, модальная матрица имеет вид:

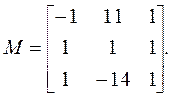
Каждый столбец данной модальной матрицы служит характеристическим вектором в одномерном векторном пространстве. Три столбца модальной матрицы образуют базис в соответствующем трехмерном векторном пространстве.

Выше рассматривалась модальная матрица при различных характеристических числах А. В случае кратных характеристических чисел и несимметрической А определение независимых модальных столбцов не очевидно, так как не существует однозначного соответствия между порядком кратности корня характеристического уравнения и дефектом соответствующей характеристической матрицы [ λ E – A ]. Однако и в этом случае вопрос построения модальной матрицы решается положительно, хотя и более сложно.

Дата добавления: 2014-12-27