Критерий согласияСтьюдента

Критерий согласияСмирнова

При оценке адекватности компьютерной модели реальной системе возникает необходимость проверки гипотезы Н₀, заключающейся в том, что две выборки принадлежат той же генеральной совокупности. Если выборки независимы и законы распределения совокупностей F(u) и F(z), из которых извлечены выборки, являются непрерывными функциями своих аргументов, то для проверки гипотезы Н₀ можно использовать критерий согласия Смирнова, при­менение которого сводится к следующему. По имеющимся результатам вычисляют эмпирические функции распределения F_э(u) и F_э(z) и определяют

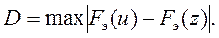
Затем при заданном уровне значимости γ находят допустимое отклонение

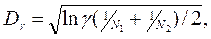
где N₁ и N₂ – объемы сравниваемых выборок для F_э(u) и F_э(z), и проводят сравнение значений D и D _γ: если D>D_γ, то нулевую гипотезу Н₀ о тождественности законов распределения F(u) и F(z) с доверительной вероятностью β= 1– γ от­вергают.

Сравнение средних значений двух независимых выборок, взятых из нормальных совокупностей с неизвестными, но равными диспер­сиями D[ν]=D[ξ], сводится к проверке нулевой гипотезы Н₀: Δ=u–z=0 на основа­нии критерия согласия Стьюдента (t -критерия). Проверка по этому критерию сводит­ся к выполнению следующих действий. Вычисляют оценку:

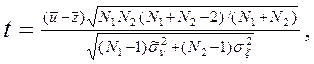
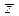где N₁ и N₂ – объемы выборок для оценки и соответственно; 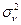и 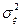– оценки дисперсий соответствующих выборок.

Затем определяют число степеней свободы k=N₁+N₂ выбирают уровень значимости γ и по таблицам находят значение t_γ. Расчетное значение t сравнивается с табличным t_γ и если | t | < t_γ, то гипотеза Н₀ не опровергается результатами компьютерного эксперимента.

Дата добавления: 2014-12-27