Регрессионный анализ результатов моделирования

Регрессионный анализ дает возможность построить модель, наилучшим об­разом соответствующую набору данных, полученных в ходе компьютерного эксперимента. Под наилучшим соответствием понимается минимальное значение функции ошибки, которая представляет собой раз­ность между прогнозируемой моделью и данными эксперимента.

Такой функцией ошибки при регрессионном анализе служит сумма квадратов ошибок.

Пример. Рассмотрим особенности регрессионного анализа результатов моделирования при построении линейной регрессионной модели. На рис. 10.5 показаны точки (x_i, у_i), i= 1,2,…, N, полученные в компьютерном эксперименте с моделью системы.

Предположим, что мо­дель результатов компьютерного эксперимента графически может быть представлена в виде прямой линии ŷ=φ(x)=b₀+b₁x, где ŷ – величина, предсказываемая регрессионной моделью.

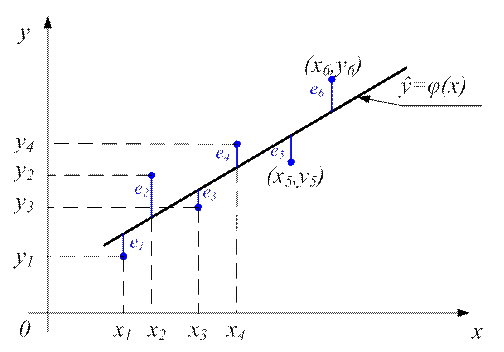
Рис. 10.5. Экспериментальные точки и линия регрессии

Требуется получить такие зна­чения коэффициентов b₀ и b₁, при которых сумма квадратов ошибок является минимальной. На рис. 10.5 ошибка e_i, i= 1,2,…, N для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки по линии регрессии ŷ=φ(x).

Для каждой линии ŷ_i=b₀+b₁x_i, i= 1,2,…, N соответствующие выражения для ошибок будут иметь вид: e_i = ŷ_i-y_i = b₀+b₁x_i – y_i, а функция ошибки будет равна

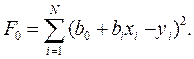
Для того чтобы минимизировать эту функцию ошибки, следует записать необходимые условия экстремума для неизвестных параметров b₀ и b₁:

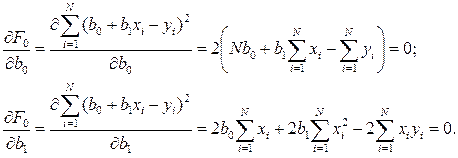
Решение этой системы двух линейных алгебраических уравнений дает значения b₀ и b₁, минимизирующие функцию ошибки.

Представив данные уравнения в матричном виде

отсюда получим:

где N – число реализаций при моделировании системы.

Часто в качестве меры ошибки регрессионной модели используется среднее квадратичное отклонение

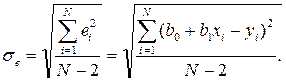
Для нормально распределенных процессов приблизительно 67% точек находится в пределах одного среднеквадратичного отклонения σ_e от линии регрессии и 95% – в пределах двух отклонений 2σ_e.

Для проверки точности оценок b₀ и b₁ регрессионной модели можно использовать критерии Фишера или Стьюдента. Подобным образом оцениваются коэффициенты уравнения регрессии и для случая нелинейной аппроксимации.

10.4.3. Дисперсионный анализ результатов моделирования

При обработ­ке и анализе результатов моделирования часто возникает задача сравнения средних выборок. Если в результате такой проверки окажется, что математическое ожидание совокупностей случайных переменных { у ⁽¹⁾}, { у ⁽²⁾},..., { у ⁽ⁿ⁾} отличается незначительно, то статистический материал, полученный в результате моделирования, можно считать однородным (в случае равенства двух первых моме­нтов). Это дает возможность объединить все совокупности в одну и позволяет существенно увеличить информацию о свойствах ис­следуемой модели, а следовательно, и самой системы. Попарное использование для этих целей критериев Смирнова и Стьюдента для проверки нулевой гипотезы затруднено в связи с наличием большого числа выборок при моделировании системы. Поэтому для этой цели используется дисперсионный анализ.

Пример. Рассмотрим решение задачи дисперсионного анализа при обработке результатов моделирования системы в следующей постановке. Пусть генеральные совокупности случайной величины { у ⁽¹⁾}, { у ⁽²⁾},..., { у ⁽ⁿ⁾} имеют нормальное рас­пределение и одинаковую дисперсию. Необходимо по выборочным средним значениям при некотором уровне значимости γ проверить нулевую гипотезу Н₀ о равенстве математических ожиданий. Выявим влияние на результаты моделирования только одного фактора, т. е. рассмотрим однофакторный дисперсионный анализ.

Допустим, изучаемый фактор х привел к выборке значений неслучайной величины Y следующего вида: y₁,y₂,…, y_k, где k – количество уровней фактора x. Влияние фактора будет оцениваться неслучайной величиной D_x, которая называется факторной дисперсией:

где 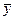– среднее арифметическое значение величины Y.

Если генеральная дисперсия D [ y ] известна, то для оценки случайного разброса наблюдений необходимо сравнить D [ y ] с выборочной дисперсией , используя критерий Фишера (F -распределение). Если эмпирическое значение F_э попадает в критическую область, то влияние фактора x считается значимым, а разброс значений x – неслучайным. Если генеральная дисперсия D [ x ] до проведения компьютерного эксперимента с моделью неизвестна, то при моделировании необходимо найти ее оценку.

Пусть серия наблюдений на уровне y_i имеет вид: y _i1,y_i2,…, y_in, где n – число повторных наблюдений на i -м уровне. Тогда на i -м уровне среднее значение наблюдений равно:

а среднее значение наблюдений по всем уровням будет равно:

Общая выборочная дисперсия всех наблюдений вычисляется в соответствии с выражением:

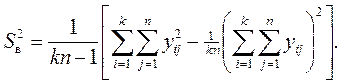
При этом разброс значений y определяется суммарным влиянием случайных причин и фактора x. Задача дисперсионного анализа состоит в том, чтобы разложить общую дисперсию D [ y ] на составляющие, связанные со случайными и неслучайными причинами.

Оценка генеральной дисперсии, связанной со случайными факторами, будет определяться следующим образом:

а оценка факторной дисперсии

Факторная дисперсия наиболее заметна при анализе средних значений на i -м уровне фактора, а остаточная дисперсия (дисперсия случайности) для средних значений в n раз меньше, чем для отдельных измерений, поэтому можно найти более точную оценку выборочной дисперсии:

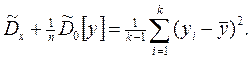
Умножив обе части этого выражения на n, получим в правой части выборочную дисперсию , имеющую (k– 1) степень свободы. Влияние фактора x будет значимым, если при заданном γ выполняется неравенство:

Иначе влиянием фактора x на результаты моделирования можно пренебречь и считать нулевую гипотезу H₀ о равенстве средних значений на различных уровнях справедливой (критерий Фишера).

Дисперсионный анализ позволяет вместо проверки нулевой гипотезы о равенстве средних значений выборок проводить при обработке результатов моделирования проверку нулевой гипотезы о тождественности выборочной и генеральной дисперсий. Дисперсионный анализ часто применяется при сравнительных исследованиях эффекта, получаемого, например, от различных методов лечения, обработки почвы, обучения и т.п.

Возможны и другие подходы к анализу и интерпретации результатов моделирования, но при этом необходимо помнить, что их эффективность существенно зависит от вида и свойств конкретной моделируемой системы.

П р и м е р и с с л е д о в а н и я САУ, п о д в е р ж е н н о й

д е й с т в и ю с л у ч а й н ы х в о з м у щ е н и й

Пример. Моделирование стохастической САУ в программном комплексе МВТУ 3.5 и обработка результатов с помощью статистической процедуры однофакторного дисперсионного анализа.

На рис. 10.6 приведена оптимизированная по квадратичному критерию модель системы автоматического управления гашением колебаний груза на подвесе [11], описываемая уравнениями состояния:

,

,

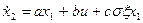где , , , ,

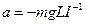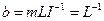
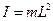σξ – помеха, действующая на точку подвеса с интенсивностью σ,

m – масса груза, g – ускорение свободного падения, L – длина подвеса.

Оптимальные значения коэффициентов синтезированного регулятора:

к₁ = –0,8552; к₂ =0,0922 получены для уровня помехи σ= 1 м/с²и длины подвеса L= 4 м.

Рис. 10.6. Модель САУ гашением колебаний груза на подвесе.

Схема моделирования возмущения по параметру a показана на рис. 10.7. Сигнал помехи, используемый в схеме, имеет вид, показанный на графике рис. 10.8.

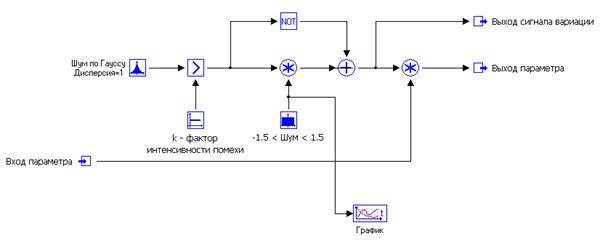
Рис. 10.7. Модель возмущения по параметру.

Рис. 10.8. Исходный сигнал помехи.

Применительно к рассматриваемому примеру САУ гашением колебаний груза на подвесе в качестве фактора влияния A может быть принят порог срабатывания логического элемента в схеме моделирования (в дальнейшем – параметр k), влияющий на интенсивность вариации сигнала возмущения по параметру системы a(t). В качестве его уровней можно принять различные значения порога, а результирующим признаком считать какой-либо из показателей качества переходных процессов: например, время регулирования или такой интегральный показатель качества как среднеквадратическое отклонение (СКО).

Для того чтобы качественным образом оценить работу данной САУ, оптимально настроенной на подавление внешнего возмущения в виде нормально распределенного шума, достаточно визуально сравнить графики выходного сигнала – угла φ(t) отклонения подвеса от вертикали для случаев отсутствия и наличия возмущения по параметру (рис. 10.9).

Рис. 10.9. Переходные процессы в САУ гашением колебаний.

Видно, что система быстро справляется с внешним возмущением при отсутствии других возмущений (график 1). При дополнительном действии возмущения по параметру переходный процесс затухания колебаний значительно ухудшается (график 2), однако САУ за счет обратных связей продолжает бороться с возмущениями: колебания значительно медленнее, но все же затухают. Характер изменения текущего значения СКО для процессов изменения угла с рис. 10.9 показан на рис. 10.10.

Рис. 10.10. СКО, соответствующие процессам изменения угла отклонения подвеса.

Реализации вызванного сбоем прерывания сигнала в линии связи, обусловившие переходные процессы на рис. 10.9, приведены на рис. 10.11.

Рис. 10.11. Сигналы в линии связи, повлиявшие на процессы, показанные на рис. 10.9

С целью получения объективной количественной оценки для рассматриваемого примера проведена серия экспериментов моделирования и реализована процедура однофакторного дисперсионного анализа. В качестве результирующего признака взята среднеквадратическая ошибка переходного процесса по углу отклонения подвеса от вертикали, а в качестве фактора – параметр модели k, влияющий на случайную частоту и амплитуду сбоев в соединительной линии связи. Уровни фактора выбраны следующие: k ={1,5; 1,25; 1,0;0,75;0,5}. При размере каждой из выборок N =20 для числа степеней свободы рассеивания за счет данного фактора m =4 и остаточного рассеивания за счет случайных ошибок наблюдений l =95 выборочная факторная и остаточная дисперсия соответственно равны S_k² =1472,47; S_ост²= 556,77. Выборочная статистика F_в= S_k²/ S_ост² =2,65 для уровня значимости γ =0,05 превышает табличное критическое значение F_кр =2,46 распределения Фишера, поэтому гипотеза о равенстве влияний различных уровней фактора k на математическое ожидание результирующего признака (СКО переходного процесса) не принимается.

Зависимость средних значений результирующего признака от уровней фактора, подтверждающая сделанный вывод, показана на графике рис. 10.12.

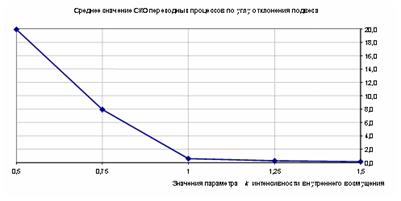
Рис. 10.12. Зависимость средних значений СКО от фактора k по результатам экспериментов

Дата добавления: 2014-12-27