КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи по минимизации и доопределению булевых функций
|
|
|
|
1. Из заданного множества А элементарных конъюнкций выделить простые импликанты функции f:
1) A = 
, 
= (00101111);
2) A =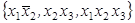 
, = (01111110);
3) A = 
, 
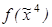= (1010111001011110);
4) A = 
, 
= (1011);
5) A = 
, = (00111011);
6) A = 
, = (00101111).
2. По заданной ДНФ с помощью метода Блейка построить сокращенную ДНФ:
1) 
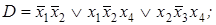
2) 
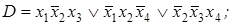
3) 
4) 
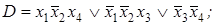
5) 
6) 
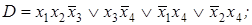
7) 
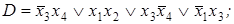
8) 
3. Построить сокращенную ДНФ по заданной КНФ:
1) 
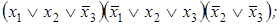
2) 
3) 
4) 
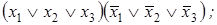
5) 
6) 
7) 
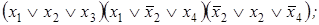
8) 
4. Изобразив множество Nf функции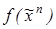 
в En, найдйте коды максимальных интервалов и построитьйте сокращенную ДНФ:
1) 
= (11110100); 2) = (01010011);
3) = (11010011); 4) = (11100111);
5) = (1111100001001100); 6) = (0001011111101111);
7) = (1110011000000111); 8) = (1111111111111000).
5. С помощью алгоритма Квайна построить сокращенную ДНФ для функции f, заданной вектором своих значений:
1) = (01110110); 2) = (10111101);
3) = (00101111); 4) = (11100100);
5) = (0001101111011011); 6) = (0000111111110110);
7) = (1111111101111110); 8) = (0000111101111111).
6. Найти сокращенную ДНФ функции f с помощью минимизирующей карты:
1) = (01010111); 2) = (11011011);
3) = (10110000); 4) = (11101111);
5) = (0001101111011111); 6) = (0011110111111101);
7) = (0011110111011110); 8) = (0010101111011111).
7. С помощью минимизирующих карт построить сокращенную ДНФ для частично определенной функции f, заданной векторно (прочерки соответсвуют неопределенным значениям):
1) = (01--01-1);
2) = (1-01--10);
3) = (1---0-10);
4) = (0--10-1-);
5) = (10-1-011-0--1-01);
6) = (0--1---0--1-1-01);
7) = (--01-1-00----1-0);
8) = (-10-1-11-01-0---).
8. Найти длину сокращенной ДНФ функции f:
1) 
2) 
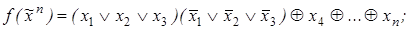
3) 
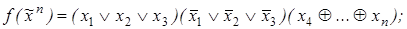
4) 
5) 
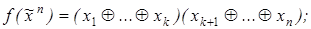
6) 
7) 
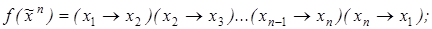
8) 
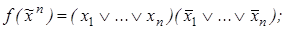
9) 
9. Выяснить, является ли ДНФ D а) тупиковой, б) кратчайшей, в)минимальной:
1) 
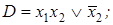
2) 
3) 
4) 
5) 
6) 
7) 
8) 
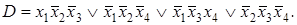
10. Применить алгоритм упрощения к ДНФ:
1) 
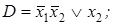
2) 
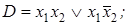
3) 
4) 
5) 
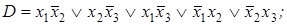
6) 
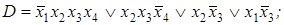
7) 
8) 
11. По заданной сокращенной ДНФ D построить минимальные ДНФ:
1) 
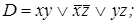
2) 
3) 
4) 
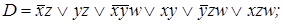
5) 
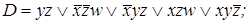
6) 
7) 
8) 
12. С помощью таблицы Квайна построить все тупиковые ДНФ функции f, заданной вектором своих значений:
1) = (01111100); 2) = (01111110);
|
|
|
3) = (00011111); 4) = (1111100001001100);
5) = (1110100001101000); 6) = (1110011000010101);
7) = (0001011110101110); 8) = (0001101111100111).
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 392; Нарушение авторских прав?; Мы поможем в написании вашей работы!