
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Задачи по алгебре высказываний
|
|
|
|
1. Записать следующие высказывания в виде пропозициональных форм, употребляя пропозициональные буквы для обозначения атомарных высказываний, т.е. таких высказываний, которые не построены из каких-либо других высказываний.
a) Если мистер Джонс счастлив, то миссис Джонс несчастлива, и если мистер Джонс несчастлив, то миссис Джонс счастлива.
b) Или Сэм пойдет на вечеринку, и Макс не пойдет на нее; или Сэм не пойдет на вечеринку и Макс отлично проведет время.
c) Необходимое и достаточное условие счастья для шейха состоит в том, чтобы иметь вино, женщин и услаждать свой слух пением.
d) Фиорелло ходит в кино только в том случае, когда там показывают комедию.
e) Для того, чтобы X было нечетным, достаточно, чтобы X было простым.
f) Необходимым условием сходимости последовательности S является ограниченность S.
g) Взятку платят тогда и только тогда, когда товар доставлен.
h) “Гиганты” выиграют приз, если “Хитрецы” сегодня не выиграют.
i) Если X положительно, то X 2 положительно.
2. Определить, является ли каждая из следующих форм тавтологией, противоречием или не является ни тем, ни другим:
а)
a) A º(A Ú A);
b) (A ® B)® ((B ® C)® (A ® C));
c) ((A ® B)& B)) ® A;
d) (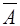 )® (A & B);
)® (A & B);
e) A &( );
);
f) (A ® B)º((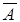 )
) 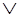 B);
B);
g) (A ® B)º  .
.
3. Выяснить, являются ли следующие рассуждения логически правильными: для этого нужно представить каждое предложение в виде пропозициональной формы и проверить, является ли заключение логическим следствием конъюнкции посылок.
а) Если Джонс – коммунист, то Джонс – атеист. Джонс – атеист, следовательно, Джонс – коммунист.
б) Если строить противоатомные убежища, то другие государства будут чувствовать себя в опасности, а наш народ получит ложное представление о своей безопасности. Если другие страны будут чувствовать себя в опасности, то они смогут начать превентивную войну. Если наш народ получит ложное представление о своей безопасности, то он ослабит свои усилия, направленные на сохранение мира. Если же не строить противоатомные убежища, то мы рискуем иметь колоссальные потери в случае войны. Следовательно, либо другие страны могут начать превентивную войну, и наш народ ослабит свои усилия, направленные на сохранение мира, либо мы рискуем иметь колоссальные потери в случае войны.
4. Проверить совместимость каждого из множества утверждений. Для этого представить предложения в виде пропозициональных форм и затем проверить, является ли их конъюнкция противоречием.
а) Если вечер скучен, то или Алиса начинает плакать, или Анатоль рассказывает смешные истории. Если Сильвестр приходит на вечер, то или вечер скучен, или Алиса начинает плакать. Если Анатоль рассказывает смешные истории, то Алиса не плачет. Сильвестр приходит на вечер тогда и только тогда, когда Анатоль рассказывает смешные истории. Если Алиса начинает плакать, то Анатоль рассказывает смешные истории.
б) Если курс ценных бумаг растет или процентная ставка снижается, то либо падает курс акций, либо налоги не повышаются. Курс акций понижается тогда и только тогда, когда растет курс ценных бумаг и налоги растут. Если процентная ставка снижается, то либо курс акций не понижается, либо курс ценных бумаг не растет. Либо повышаются налоги, либо курс акций понижается и снижается процентная ставка.
5. Каково наибольшее число утверждений из приводимых ниже, которые одновременно могут быть истинными:
a) Джо ловкач;
b) Джо не везет;
c) Джо везет, но он не ловкач;
d) если Джо ловкач, то ему не везет;
e) Джо является ловкачом тогда и только тогда, когда ему везет;
f) либо Джо ловкач, либо ему везет, но не то и другое одновременно.
6. a и b – целые положительные числа. Известно, что из следующих четырех утверждений:
a) a +1 делится на b;
b) a равно 2 b +5;
c) a + b делится на 3;
d) a +7 b – простое число;
e) три верных, а одно не верное. Найдите все возможные пары a, b.
7. Найти натуральное число A, если из следующих утверждений два верны, а одно не верно:
a) A +51 есть точный квадрат;
b) последняя цифра числа A есть единица;
c) A +7 есть точный квадрат.
8. Некая страна населена жителями, каждый из которых либо всегда говорит правду, либо всегда лжет и которые отвечают на вопросы только посредством “да” или “нет”. К развилке дорог, из которых одна ведет в столицу, а другая туда не приводит, приходит турист. Никаких знаков, указывающих, какую дорогу следует выбрать, при развилке нет. Зато здесь стоит местный житель, некто господин Р. Какой вопрос, требующий ответа “да” или “нет”, должен задать турист, чтобы выбрать верную дорогу?
Указание. Пусть A означает высказывание “господин р. всегда говорит правду”, а B обозначает высказывание “дорога идущая налево, ведет в столицу”. С помощью подходящей таблицы истинности построить такую пропозициональную форму, содержащую A и B, чтобы ответ местного жителя на вопрос, истина ли эта пропозициональная форма, гласил “да” тогда и только тогда, когда B истинно.
9. Найти число X, если в каждом из трех утверждений о числе X верна только половина.
a) X – число иррациональное, равное площади правильного треугольника со стороной a = 2.
b) X – число, кратное 4 и равное радиусу окружности, длина которой равна 2.
c) X < 3 и равно диагонали квадрата, сторона которого равна 2.
10. Три купчихи: Олимпиада, Анфиса и Пелагея пили чай. Если бы Олимпиада выпила на 5 чашек чая больше, то она выпила бы столько, сколько Анфиса и Пелагея вместе. Если бы Анфиса выпила на 9 чашек чая больше, то она выпила бы столько, сколько Олимпиада и Пелагея вместе. Их отчества: Титовна, Уваровна, Карповна. Определить, сколько выпила чашек чая каждая из них и у какой какое отчество, если известно, что Титовна выпила число чашек кратное трем, а Карповна выпила 11 чашек.
11. Три колхозника: Петр, Павел и Андрей и их жены Екатерина, Мария и Валентина отправились в кооператив. Каждый из шести лиц купил столько вещей, сколько рублей заплатил за каждую вещ. Петр купил 23 вещами более чем Мария, а Павел – 11 вещами более, чем Екатерина. Известно, кроме того, что каждый муж издержал на 63 рубля больше чем его жена. Определить имя жены каждого колхозника.
12. Алиса сказала, что Барбара и Клара говорят правду, а Клара сказала, что Элспет и Фиона или обе говорят правду, или обе лгут. С другой стороны, Деби считает, что по крайней мере или Алиса, или Барбара говорят правду, тогда как Барбара утверждает, что только одна из двух – Алиса или Фиона – была правдивой. Элспет считает, что Алиса и Барбара всегда говорят правду, однако Фиона уверена, что Барбара и Клара обе не могли сказать правду. Кому мы должны верить?
13. Организаторы международной конференции по компьютерам решили, что для того чтобы на встрече не доминировали коммерческие интересы, будет только один магазин, которым будут пользоваться вместе все производители компьютеров. Сами производители будут ответственны за определение того, кто принимает участие в представительстве. Десять компаний – пять европейских и пять американских – дали знать, что они хотят принять участие в конференции. (Обозначим эти компании через A, D, C, D, E и F, G, H, I, J соответственно.) Однако из-за обязательств по контрактам и торговой политике должны появиться различные ограничения. Европейские предписания требуют, чтобы G и I не могли одновременно принимать участие в конференции; аналогично не могут одновременно принять участие F, G и J. Ограничения американских производителей исключают участие A и D, пока G не примет участия; аналогично исключаются C и D Если E присутствует на конференции, то должно присутствовать и J, однако если они принимают участие вдвоем, то B не может быть там. И наконец, B и C не могут вместе принимать участие в конференции.
Может ли быть достигнуто соглашение, по которому по три компании из каждой группы могут собраться вместе, не нарушая условий? Если так, то кто именно примет участие?
14. На острове живут два племени: молодцы, которые всегда говорят правду, и лжецы, которые всегда лгут. Путешественник встретил туземца, спросил его, кто он такой, и, когда услышал, что он из племени молодцов, нанял его в услужение. Они пошли и увидели вдали другого туземца, и путешественник послал своего слугу спросить его, к какому племени он принадлежит. Слуга вернулся и сказал, что тот утверждает, что он из племени молодцов. Спрашивается, был ли слуга молодцом или же лгуном.
15. В перерыве в классе осталось 15 учащихся. В это время там разбили окно. Учитель записал высказывания отдельных учащихся.
Аня: Я этого не делала; сделал это Борис.
Борис: Да я его разбил.
Ваня: Он лжет, это сделал Закир.
Даша: Нет, это не так, но я этого также не делала.
Ева: Это сделала либо Катя, либо Аня, но не я.
Закир: Окно разбила одна из девочек.
Женя: Ничуть его разбили мальчики.
Соня: Это сделали мы с Аней.
Ира: Я видела, как его разбил один из мальчиков, но не помню кто.
Яша: Борис говорит неправду, окно разбил я.
Катя: Я в этом не участвовала, Аня это сделала одна.
Лева: Яша сказал правду.
Маня: Лева врет окно разбилось само от ветра.
Надя: Я читала книгу и ничего не знаю.
Роза: Это сделала Аня.
Если один и только один из учащихся говорил правду, кто разбил окно?
16. В перерыве в классе оставалось девять учеников. Один из них разбил окно. На вопрос учителя были получены следующие ответы.
Яша: Это сделал Владик.
Борис: Это не правда.
Маня: Я его разбила.
Ваня: Сделала это либо Маня, либо Аня.
Владик: Борис лжет.
Степа: Это сделала Маня.
Леня: Нет, Маня окно не разбивала.
Аня: Ни Маня, ни я этого не делали.
Роза: Аня права, но и Владик тоже не виновен.
Если из этих девяти показаний истинны только три, то кто разбил окно?
17. Брауну, Джонсу и Смиту предьявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники были на синем «Бьюике», Джонс сказал, что это был черный «Крайслер», а Смит утверждал, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что желая запутать следствие, каждый из них указал правильно либо только марку машины, либо ее цвет. Какого цвета был автомобиль, и какой марки?
18. Профессор Икс Игрекович Зет был, как известно, так же учен, как и рассеян. У него была большая библиотека, которая помещалась в трех комнатах. В первой были справочники, во второй – труды по его специальности, в третьей – научные журналы. Когда он писал свой знаменитый труд «О бессмертии майских жуков», у него на столе царил невероятный хаос, и он не мог найти трех вещей: словарь эскимосского языка, учебник носологии и памфлет своего заклятого противника доктора Болтунова. Профессор страшно взволновался и обвинил лаборанта, что тот, по-видимому, поставил словарь где-то среди трудов, а учебник и памфлет – среди журналов. Лаборант отрицал это и говорил, что профессор, как всегда, бросил все три вещи куда-нибудь на полку в первой комнате. А супруга профессора высказала предположение, что словарь, вероятно, находится среди журналов, а учебник и памфлет – среди трудов. Каждый настаивал на своем, началась бурная перебранка. Дочь профессора, слушавшая это, сказала: «Все, что вы утверждаете, неверно». Если она была права, куда затерялись эти вещи?
19. Согласно договоренности, порядок утверждения нового проекта, в разработке которого участвуют учреждения А, Б, В, таков: если в утверждении принимают сначала учреждения А и Б, то должно присоединиться к участию и учреждение В. Если утверждение проходит сначала в учреждениях Б и В, присоединяется и учреждение А. Спрашивается, возможны ли такие случаи при утверждении проекта, когда принимали бы в нем участие только учреждения А и В, между тем как участие учреждения Б не было бы необходимо (при сохранении договоренности о порядке утверждения проектов)?
20. Турист шел к озеру. Он шел до перекрестка, откуда вела одна дорога вправо, а другая – влево; одна шла к озеру, другая – нет. На перекрестке сидело двое парней, один из них всегда говорил правду, второй всегда лгал. Оба они отвечали на любой вопрос либо «да», либо «нет». Все это было туристу известно, но он не знал, кто из них говорит правду, кто лжет; он также не знал, какая из дорог ведет к озеру.
а) Турист поставил обоим сразу один вопрос, каждый из них дал на него свой ответ. Спрашивается, какой это был вопрос, раз турист по полученным ответам безошибочно решил, какая из дорог ведет к озеру?
б) Турист поставил одному из парней два вопроса. Какие это были вопросы, раз он по ответам на них узнал, какая дорога ведет к озеру?
в) Турист поставил лишь один вопрос одному из парней. Какой это был вопрос, раз он узнал по ответу, какая дорога ведет к озеру?
21. Самодержавный правитель одного острова хотел воспрепятствовать тому, чтобы на острове поселились пришельцы. Желая соблюсти видимость справедливости, он издал распоряжение, согласно которому всякий, желающий поселиться на острове, должен, хорошо поразмыслив, высказать любое предложение, причем после предварительного предупреждения, что от содержания этого предложения зависит его жизнь.
Распоряжение гласило: «Если пришелец скажет правду, его расстреляют. Если он скажет неправду, его повесят». Может ли пришелец, став жителем острова, сохранить свою жизнь?
22. Попытайтесь описать логические условия, выражающие деятельность контакта, включающего утюг, в связи с контактом, предохраняющим утюг от перегрева, и в связи с состоянием отопительной спирали, т.е. выяснить, какие из состояний этих трех частей утюга – включение или не включение контакта, включение или не включение предохранителя, перегрев или не перегрев спирали – совместимы друг с другом, а какие из состояний не совместимы друг с другом.
Список литературы
1. Яблонский С.В. Введение в дискретную математику. – М.: Наука, 1986. –384 с.
2. Нефедов В.Н., Осипова В.А. Курс дискретной математики – М.: Издательство МАИ, 1992. –264с.
3. Мендельсон Э. Введение в математическую логику. – М.: Наука, 1984. –319с.
4. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дискретной математики. – М.: Наука, 1992. –408с.
5. Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач на алгебре и теории чисел. – М.: Просвещение, 1993.
6. Набебин А.А. Логика и пролог в дискретной математике. – М.: МЭИ, 1996. –452с.
7. Кольман Э. Зих О. Занимательная логика. – М.: Наука, 1966. –127с.
8. Сборник конкурсных задач по математике для поступающих во втузы./Под ред. Сканави М.И. – М.: Высшая школа, 1980. –541с.
9. Рембольд У. Введение в информатику для научных работников и инженеров. – Уфа: УГАТУ, 1996. –445с.
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 2250; Нарушение авторских прав?; Мы поможем в написании вашей работы!