
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные виды записи задач линейного программирования 2 страница
|
|
|
|
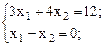
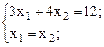
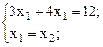
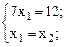
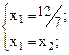

Тогда: 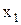 =
=  ;
;  =
=  и max Z= –
и max Z= – 
Ответ: Z= –  в
в 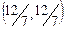 .
.
Пример 2. Решить ЗЛП графическим методом. Найти:
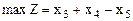
при
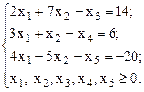
Решение.
Задачи, представленные в канонической форме можно решать графическим методом только в том случае, если разность между порядком и рангом системы ограничений равна 2. В данном случае: 5-3=2.
Представим задачу таким образом, чтобы можно было решать графическим методом. Для этого в системе ограничений выразим переменные 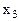 ,
, 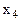 и
и 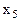 через
через 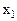 и
и 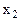 .
.
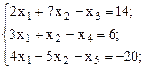

Так как все переменные неотрицательны, то можно составить систему неравенств:
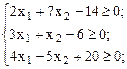
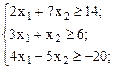
Подставим в целевую функцию вместо 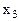 ,
, 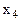 и
и 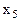 соответственные значения:
соответственные значения:

Таким образом, ЗЛП имеет вид:

при
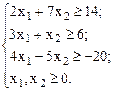
Найдем градиент: 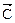 (1;1).
(1;1).
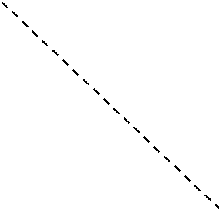
Построим область допустимых значений. Для этого построим прямые, соответственные ограничениям:
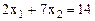
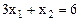

| 1: | A | B | 2: | A | B | 3: | A | B | ||
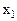
| 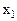
| 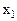
| -5 | |||||||
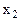
| 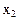
| 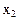
|
| y | |||||||||||||||

| 
| ||||||||||||||

| |||||||||||||||
| |||||||||||||||

| |||||||||||||||

| |||||||||||||||

| |||||||||||||||
| x | |||||||||||||||

| |||||||||||||||
Область допустимых решений не ограничена сверху. Значит, решений нет.
Ответ: Решений нет.
2.3. Свойства решений задачи линейного программирования
Пусть ЗЛП представлена в виде:
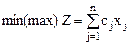
при
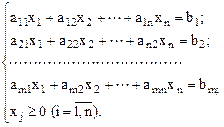
Выделим зависимость между m и n и количеством решений системы уравнений.
Пусть m>n. Количество уравнений больше числа переменных и нет линейно-зависимых уравнений. Система не имеет решений.
Если m=n и нет линейно зависимых, то система ограничений имеет единственное решение. Следовательно, ЗЛП имеет единственное решение именно в этой точке.
Если m<n, то система имеет бесконечно много решений. В данной ситуации и возникает правомерный вопрос о нахождении оптимального решения.
Запишем ЗЛП в векторном виде:

при


Пусть m<n. Все m уравнений линейно- независимы. Тогда переменные 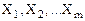 можно выразить через переменные
можно выразить через переменные 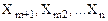 . Назовем
. Назовем 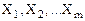 - базисными переменными, а
- базисными переменными, а 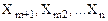 – свободными.
– свободными.
Область допустимых значений будем называть многогранником планов (для ЗЛП от двух неизвестных – выпуклый многоугольник). Точку пересечения линий будем называть крайней точкой многогранника планов.
Решая ЗЛП, мы получили некоторое решение, удовлетворяющее системе ограничений. Если свободные переменные при этом равны нулю, а базисные переменные принимают неотрицательные значения, то полученное частное решение называют опорным решением.
Теорема1. Если система векторов 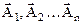 , имеет линейно-независимую подсистему
, имеет линейно-независимую подсистему 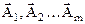 , то допустимое решение (
, то допустимое решение (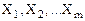 ,0,0,…,0) является крайней точкой многогранника планов.
,0,0,…,0) является крайней точкой многогранника планов.
Замечание: Среди крайних точек многогранника плана и находится оптимальное (max) решение.
Теорема2. (основная теорема линейного программирования) Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает такого же значения в любой точке, являющейся их выпуклой линейной комбинацией.
2.4. Общая идея симплексного метода
Исходя из основной теоремы линейного программирования, можно предположить следующий метод решения ЗЛП: Находятся все крайние точки многогранника планов и из них выбирается оптимальная. Метод решения универсален, но чрезвычайно трудоемок. Количество крайних точек многогранника планов можно рассчитать по формуле:
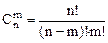 .
.
Для примера: m=5, n=7. Количество крайних точек: 21. каждую из них необходимо найти, посчитать значение целевой функции. Потом все их сравнить.
В связи с этим была поставлена проблема оптимизации перебора точек, т.е. не все точки находить, а только те, значение целевой функции в которых "лучше", чем исходное.
Таким образом, общая идея симплексного метода состоит в следующем: перемещаясь от данной крайней точки к смежной по ребру лучшей, а затем еще лучшей, найти оптимальное решение ЗЛП.
Алгоритм решения ЗЛП симплексным методом:
1. Найти начальное опорное решение ЗЛП.
2. Проверить, не является ли оно оптимальным.
3. Если решение оптимально, то ЗЛП решена. В противном случае необходимо перейти в другую крайнюю точку многогранника планов (найти другое опорное решение), которая не хуже предыдущей (значение целевой функции не хуже, чем в предыдущей точке).
4. Перейти к пункту 2.
Исходя из алгоритма решения выделим что необходимо знать и уметь при решении задач симплексным методом:
1) уметь строить начальный опорный план ЗЛП;
2) знать признак оптимальности опорного плана;
3) уметь переходить к нехудшему опорному плану.
2.5. Построение начального опорного плана при решении задач линейного программирования симплексным методом
Существует несколько приемов нахождения начального опорного плана в зависимости от вида системы ограничений.
Случай 1:
Пусть система ограничений представлена в каноническом виде:
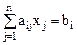 (
(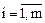 ).
).
Определение 1: Говорят, что ограничение в ЗЛП имеет предпочтительный вид, если при неотицательной правой части (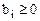 ) левая часть уравнения содержит переменную с коэффициентом 1, которая в другие уравнения системы входит с коэффициентом, равным 0.
) левая часть уравнения содержит переменную с коэффициентом 1, которая в другие уравнения системы входит с коэффициентом, равным 0.
Пример 1:
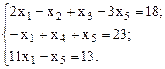
В данном примере первое и второе уравнения имеют предпочтительный вид, так как в первом есть переменная 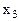 , коэффициент у которой 1, а в остальные уравнения данная переменная не входит; во втором такая переменная -
, коэффициент у которой 1, а в остальные уравнения данная переменная не входит; во втором такая переменная - 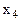 .
.
Определение 2: Переменная, входящая в одно из уравнений системы с коэффициентом, равным 1, а в остальные с коэффициентом, равным 0, называется предпочтительно переменной.
В примере 1 в первом уравнении предпочтительная переменная – 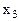 , во втором –. В третьем уравнении предпочтительных переменных нет.
, во втором –. В третьем уравнении предпочтительных переменных нет.
Определение 3: Говорят, что система уравнений имеет предпочтительный вид, если каждое уравнение системы имеет предпочтительный вид.
Если система имеет предпочтительный вид, то начальное опорное решение находится следующим образом: все предпочтительные переменные будут базисными, а остальные свободными. Базисные переменные приравниваются к свободным членам, а свободные к нулю. Полученное решение является начальным опорным планом.
Пример 2:
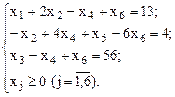
Система имеет предпочтительный вид. Предпочтительные переменные (соответственно уравнениям) 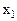 ,
, 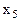 и
и 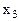 . Следовательно, решение ЗЛП имеет вид: (13, 0, 56, 0, 4).
. Следовательно, решение ЗЛП имеет вид: (13, 0, 56, 0, 4).
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 301; Нарушение авторских прав?; Мы поможем в написании вашей работы!