
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способ 2. 4 страница
|
|
|
|
Определение 2: Совокупность правил, однозначно определяющих последовательность действий стороны в конкретной конфликтной ситуации, есть стратегия.
Определение 3: Под игрой понимается совокупность предварительно оговоренных правил и условий.
Определение 4: Частичная возможная реализация правил игры называется партия.
Если n партнеров (игроков) участвуют в данной игре, то основной вопрос теории игр заключается в следующем: как должен вести себя j-ый партнер для достижения наиболее благоприятного для себя исхода?
В конце партии каждый игрок получает сумму  (
(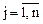 ), которую будем называть выигрышем. При этом подразумевается, что каждый игрок пытается свой выигрыш максимизировать. Числа
), которую будем называть выигрышем. При этом подразумевается, что каждый игрок пытается свой выигрыш максимизировать. Числа  (
(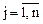 ) могут быть положительными, отрицательными и равными 0. Если выигрыш – число положительное, то игрок выиграл партию. Если выигрыш – отрицательный, то проиграл. Если выигрыш равен 0 – ничья.
) могут быть положительными, отрицательными и равными 0. Если выигрыш – число положительное, то игрок выиграл партию. Если выигрыш – отрицательный, то проиграл. Если выигрыш равен 0 – ничья.
В большинстве случаев мы будем иметь дело с играми с нулевой суммой, т.е.  . В этих играх сумма выигрыша переходит от одного игрока к другому, не поступая из дополнительных источников.
. В этих играх сумма выигрыша переходит от одного игрока к другому, не поступая из дополнительных источников.
Определение 5: Игры, в которых участвуют два игрока, называются парными, а с большим числом игроков – множественными.
Определение 6: Принятие игроком того или иного решения в процессе игры и его реализация называется ходом.
Ходы могут быть личные (ход выбран сознательно) и случайные (ход выбран на основании метода случайного выбора).
В зависимости от количества стратегий игры делятся на конечные и бесконечные. В конечной игре каждый игрок имеет конечное число стратегий, в бесконечной – бесконечное.
В зависимости от взаимоотношений игроков игры делятся на кооперативные, коалиционные и бескоалиционные. Если игроки не имеют право вступать ни в какие соглашения, то игра будет бескоалиционная. Если же они имеют право вступать в коалиции – коалиционные. Кооперативная игра – это игра, в которой заранее определены все коалиции.
В зависимости от функции выигрыша игры делятся на матричные, непрерывные, выпуклые и т.д. Мы будем рассматривать матричные игры.
Пример 1: Игра "орел – решка". Играют два игрока. Каждый игрок выбирает одну из сторон монеты: орел или решку. По очереди они бросают монету. Выигрывает тот, кто угадал выпавшую сторону монеты.
Пример 2: Игра "в три пальца". Играют два игрока. Оба игрока одновременно и независимо друг от друга показывают один, два или три пальца. Если общее количество пальцев число четное, то эту сумму выигрывает первый игрок, если нечетное, то ее выигрывает второй игрок.
В общем случае матричная игра задается прямоугольной матрицей размером m 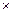 n. Номер i-ой строки соответствует номеру стратегии
n. Номер i-ой строки соответствует номеру стратегии 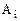 , применяемой первым игроком. Номер j-ого столбца соответствует стратегии
, применяемой первым игроком. Номер j-ого столбца соответствует стратегии  , применяемой вторым игроком. Описанная игра однозначно определяется матрицей:
, применяемой вторым игроком. Описанная игра однозначно определяется матрицей:
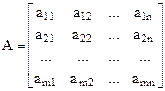 .
.
Каждый элемент  матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую вторым игроком первому, если первый игрок выбирает строку, соответствующую i-той строке, а второй игрок – j-тому столбцу.
матрицы является действительным числом и представляет собой сумму выигрыша, уплачиваемую вторым игроком первому, если первый игрок выбирает строку, соответствующую i-той строке, а второй игрок – j-тому столбцу.
Матричную игру часто записывают в развернутой форме в виде таблицы, которую называют платежной матрицей:
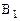
| … | 
| … | 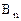
| |
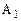
| 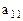
| … | 
| … | 
|
| … | … | … | … | … | |
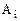
| 
| … | 
| … | 
|
| … | … | … | … | … | |

| 
| … | 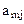
| … | 
|
Каждый игрок выбирает для себя наиболее выгодную стратегию. При этом первый игрок стремится выигрыш максимизировать, а второй – минимизировать проигрыш. В связи с этим вводятся понятия нижней и верхней цены игры.
Определение 7: Нижней чистой ценой игры (максимином) называется число α, определяемое по формуле:
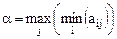 .
.
Определение 8: Верхней чистой ценой игры (минимаксом) называется число β, определяемое по формуле:
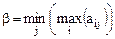 .
.
Определение 9: Стратегии игроков, соответствующие максимину (минимаксу), называются максиминными (минимаксными).
Пример 3: Найти максиминную и минимаксную стратегии игроков в матричной игре:
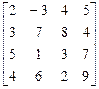
Решение.
| 
| 
| 
| 
| |
| -3 | -3 | |||

| |||||

| |||||
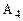
| |||||

|
4.5. Чистые и смешанные стратегии и их свойства
Различают стратегии чистые и смешанные. Чистая стратегия 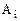
 первого игрока (чистая стратегия
первого игрока (чистая стратегия 
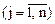 второго игрока) – это возможный ход первого (второго) игрока, выбранный им с вероятностью, равной 1.
второго игрока) – это возможный ход первого (второго) игрока, выбранный им с вероятностью, равной 1.
Если первый игрок имеет m стратегий, а второй – n стратегий, то для любой пары стратегий первого и второго игроков чистые стратегии можно представить в виде единичных векторов. Например, для пары стратегий 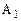 ,
,  чистые стратегии первого и второго игроков запишутся в виде:
чистые стратегии первого и второго игроков запишутся в виде:  ,
,  . Для пары стратегий
. Для пары стратегий 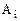 ,
,  чистые стратегии можно записать в виде:
чистые стратегии можно записать в виде:
 ,
,
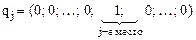 .
.
Теорема: В матричной игре нижняя чистая цена игры не превосходит верхней чистой цены игры, т. е.  .
.
Определение: Если для чистых стратегий 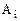 ,
,  игроков A и В соответственно имеет место равенство
игроков A и В соответственно имеет место равенство 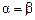 , то пару чистых стратегий (
, то пару чистых стратегий (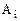 ,
,  ) называют седловой точкой матричной игры, элемент
) называют седловой точкой матричной игры, элемент  матрицы, стоящий на пересечении i-й строки и j-го столбца – седловым элементом платежной матрицы, а число
матрицы, стоящий на пересечении i-й строки и j-го столбца – седловым элементом платежной матрицы, а число 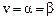 — чистой ценой игры.
— чистой ценой игры.
Пример: Найти нижнюю и верхнюю чистые цены, установить наличие седловых точек матричной игры
 .
.
Решение.
Определим нижние и верхние чистые цены игры: 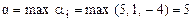 ,
,  ,
,  .
.
| В1 | В2 | В3 | В4 | 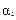
| |
| А1 | |||||
| А2 | |||||
| А3 | -4 | -4 | |||
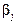
|
В данном случае имеем одну седловую точку (А1; В2), а седловой элемент равен 5. Этот элемент является наименьшим в 1-й строке и наибольшим во 2-м столбце. Отклонение игрока А от максиминной стратегии А1 ведет к уменьшению его выигрыша, а отклонение игрока В от минимаксной стратегии В2 ведет к увеличению его проигрыша. Иными словами, если в матричной игре имеется седловой элемент, то наилучшими для игроков являются их минимаксные стратегии. И эти чистые стратегии, образующие седловую точку и выделяющие в матрице игры седловой элемент a12=5, есть оптимальные чистые стратегии  и
и 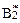 соответственно игроков А и В.
соответственно игроков А и В.
Если же матричная игра не имеет седловой точки, то решение игры затрудняется. В этих играх  . Применение минимаксных стратегий в таких играх приводит к тому, что для каждого из игроков выигрыш не превышает
. Применение минимаксных стратегий в таких играх приводит к тому, что для каждого из игроков выигрыш не превышает 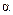 , а проигрыш — не меньше
, а проигрыш — не меньше 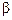 . Для каждого игрока возникает вопрос увеличения выигрыша (уменьшение проигрыша). Решение находят, применяя смешанные стратегии.
. Для каждого игрока возникает вопрос увеличения выигрыша (уменьшение проигрыша). Решение находят, применяя смешанные стратегии.
Определение: Смешанной стратегией первого (второго) игрока называется вектор 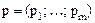 , где
, где 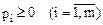 и
и  (
( , где
, где  и
и  ).
).
Вектор p(q) означает вероятность применения i-й чистой стратегии первым игроком (j-й чистой стратегии вторым игроком).
Поскольку игроки выбирают свои чистые стратегии случайно и независимо друг от друга, игра имеет случайный характер и случайной становится величина выигрыша (проигрыша). В таком случае средняя величина выигрыша (проигрыша) – математическое ожидание – является функцией от смешанных стратегий р, q:
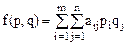 .
.
Определение: Функция f(р, q) называется платежной функцией игры с матрицей  .
.
Определение: Стратегии 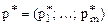 ,
,  называются оптимальными, если для произвольных стратегий
называются оптимальными, если для произвольных стратегий  ,
,  выполняется условие
выполняется условие
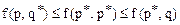
|
Использование в игре оптимальных смешанных стратегий обеспечивает первому игроку выигрыш, не меньший, чем при использовании им любой другой стратегии р; второму игроку – проигрыш, не больший, чем при использовании им любой другой стратегии q.
Совокупность оптимальных стратегий и цены игры составляет решение игры.
4.6. Свойства чистых и смешанных стратегий
Значение платежной функции при оптимальных стратегиях определяет цену игры v, т. е.  .
.
Теорема: В смешанных стратегиях любая конечная матричная игра имеет седловую точку.
Пусть имеем матричную игру 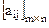 и некоторые смешанные оптимальные стратегии
и некоторые смешанные оптимальные стратегии 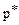 ,
,  игроков А и В, обеспечивающие сумму выигрыша v. Вопрос поставим так: как проверить, что набор
игроков А и В, обеспечивающие сумму выигрыша v. Вопрос поставим так: как проверить, что набор 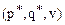 является решением игры? Для этого нужно проверить справедливость неравенства
является решением игры? Для этого нужно проверить справедливость неравенства 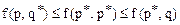 для любых смешанных стратегий, среди которых и будут стратегии
для любых смешанных стратегий, среди которых и будут стратегии 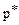 ,
,  . Однако, различных смешанных стратегий, среди которых и оптимальные, имеем бесчисленное множество. И в таком случае проверить справедливость этого неравенства невозможно. Поэтому рассмотрим следующую теорему, которая позволит ответить на поставленный выше вопрос.
. Однако, различных смешанных стратегий, среди которых и оптимальные, имеем бесчисленное множество. И в таком случае проверить справедливость этого неравенства невозможно. Поэтому рассмотрим следующую теорему, которая позволит ответить на поставленный выше вопрос.
Теорема: Для того чтобы смешанные стратегии 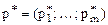 и
и  были оптимальными для игроков А и В в игре с матрицей
были оптимальными для игроков А и В в игре с матрицей  и выигрышем v, необходимо и достаточно выполнения неравенств:
и выигрышем v, необходимо и достаточно выполнения неравенств:
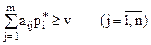
|
|
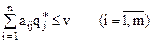 .
.
На основании данной теоремы можно сделать вывод: если игрок А применяет оптимальную смешанную стратегию 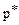 , а игрок В – любую чистую стратегию Вj, то выигрыш игрока А будет не меньше цены игры v. Аналогично: если игрок В использует оптимальную смешанную стратегию
, а игрок В – любую чистую стратегию Вj, то выигрыш игрока А будет не меньше цены игры v. Аналогично: если игрок В использует оптимальную смешанную стратегию  , а игрок А – любую чистую стратегию Ai, то проигрыш игрока В не превысит цены игры v.
, а игрок А – любую чистую стратегию Ai, то проигрыш игрока В не превысит цены игры v.
Чистые стратегии игрока, входящие в его оптимальную смешанную стратегию с вероятностями, отличными от нуля, называются активными стратегиями игрока. Рассмотрим теорему об активных стратегиях.
Теорема: Если один из игроков придерживается своей оптимальной смешанной стратегии, то его выигрыш остается неизменным и равным цене игры независимо от того, какую стратегию применяет другой игрок, если только тот не выходит за пределы своих активных стратегий.
На основании данной теоремы решение матричной игры можно упростить, выявив при этом доминирование одних стратегий над другими. Так, рассматривая стратегии игрока А, сравниваем элементы строк s и t, а именно: 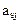 с элементами аtj для
с элементами аtj для 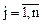 . Если
. Если 
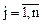 , то выигрыш игрока А при стратегии Аs будет больше, чем при стратегии At. В этом случае стратегия Аs доминирует над стратегией At. Стратегию Аs называют доминирующей, а стратегию At — доминируемой.
, то выигрыш игрока А при стратегии Аs будет больше, чем при стратегии At. В этом случае стратегия Аs доминирует над стратегией At. Стратегию Аs называют доминирующей, а стратегию At — доминируемой.
Поскольку игрок В заинтересован в минимизации проигрыша, доминирующим будет столбец с наименьшими элементами. Например, сравниваем элементы r-гo и l-го столбцов. Если все элементы 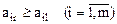 , то игроку В свой выбор выгодно сделать по l-му столбцу. В этом случае стратегия Вl игрока В доминирует над стратегией Вr. Стратегия Вl называется доминирующей, а стратегия Вr — доминируемой.
, то игроку В свой выбор выгодно сделать по l-му столбцу. В этом случае стратегия Вl игрока В доминирует над стратегией Вr. Стратегия Вl называется доминирующей, а стратегия Вr — доминируемой.
Если в матричной игре имеем строки (столбцы) с одними и теми же элементами, то строки (столбцы), а соответственно и стратегии игроков А и В, называются дублирующими.
В матричной игре доминируемые и дублирующие строки (столбцы) можно опускать, что не влияет на решение игры.
Теорема: Оптимальные смешанные стратегии 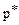 и
и  соответственно игроков А и В в матричной игре
соответственно игроков А и В в матричной игре  с ценой v будут оптимальными и в матричной игре
с ценой v будут оптимальными и в матричной игре 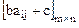 с ценой
с ценой  , где
, где  .
.
На основании данной теоремы платежную матрицу, имеющую отрицательные числа, можно преобразовать в матрицу с положительными числами.
Пример: Выполнить всевозможные упрощения матричной игры

Решение.
Поскольку соответствующие элементы второй и четвертой строк матрицы игры равны, т. е. имеем две дублирующие строки, опустим, например, четвертую строку.

Сравним соответствующие элементы столбцов. Элементы первого столбца доминируют над элементами третьего и шестого столбцов, а элементы второго столбца доминируют над соответствующими элементами четвертого столбца. Игроку В невыгодно применять стратегии В3, B4 и В6. Опускаем третий, четвертый и шестой столбцы и получаем матрицу вида
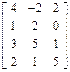
Элементы второй строки меньше соответствующих элементов третьей строки. Следовательно, игроку А невыгодна стратегия А2. Опуская вторую строку, получаем упрощенную матрицу

Если требуется получить матрицу с положительными элементами, то достаточно прибавить к ее элементам, например, число 2.
На примере покажем один из методов нахождения решения игры, заданной матрицей.
Пример: Найти решение игры, заданной матрицей

Решение.
Проверим наличие седловых точек. Найдем минимальные элементы в каждой из строк (2; 4) и максимальные в каждом из столбцов (6; 5). Значит, нижняя цена игры α=max(2; 4)=4 и β=min(6;5)=5. Так как α≠β, то решением игры являются смешанные оптимальные стратегии, а цена игры заключается в пределах от 4 до 5.
Предположим, что для игрока А стратегия задается вектором 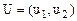 . Тогда средний выигрыш при первой и второй стратегии будет равен:
. Тогда средний выигрыш при первой и второй стратегии будет равен:
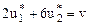 ,
,
 .
.
Вероятность выбора той или иной стратегии равна 1, т.е.
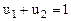 .
.
Получим систему из трех уравнений с тремя неизвестными. Решив ее получим  ,
,  и
и 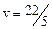 .
.
 Построим геометрическую иллюстрацию данного метода решения.
Построим геометрическую иллюстрацию данного метода решения.
Откладываем на оси 0u единичный отрезок. Строим линию параллельно оси 0z. Строим прямые через точки (2; 6) и (5; 4). Линии пересекаются в точке М.
Полученные линии и разбиение единичного отрезка на две части дает возможность составления системы уравнений, которую мы приводили выше.
Ответ:  ,
,  и
и 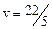 .
.
Обобщая изложенные выше результаты нахождения решения игры 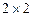 , можно указать основные этапы нахождения решения игры
, можно указать основные этапы нахождения решения игры 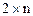 или
или  .
.
1. Строим прямые, соответствующие стратегиям одного игрока.
2. Определяем нижнюю (верхнюю) границу выигрыша.
3. Находят две стратегии этого игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) координатой.
4. Определяем цену игры и оптимальные стратегии.
4.7. Приведение матричной игры к ЗЛП
Покажем как привести матричную игру размерности 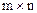 с матрицей А к задаче линейного программирования.
с матрицей А к задаче линейного программирования.
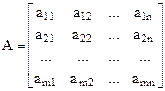
Обозначим через 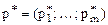 и
и  оптимальные смешенные стратегии игроков А и В. Стратегия
оптимальные смешенные стратегии игроков А и В. Стратегия 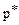 игрока А гарантирует ему выигрыш не меньше v, все зависимости от выбора стратегии игроком В. Это можно записать так:
игрока А гарантирует ему выигрыш не меньше v, все зависимости от выбора стратегии игроком В. Это можно записать так:

Причем  ,
,  (
(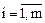 ).
).
Аналогично стратегия  игрока В гарантирует ему проигрыш не больше v, независимо от выбора стратегии игроком А.
игрока В гарантирует ему проигрыш не больше v, независимо от выбора стратегии игроком А.

Причем 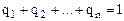 ,
, 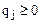 (
(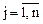 ).
).
Разделим обе части неравенств на положительное число v (обе системы) и произведем замену: 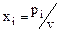 ,
,  (
(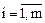 ,
, 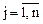 ). Получим:
). Получим:

Причем 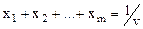 ,
,  (
(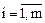 ).
).

Причем  ,
, 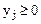 (
(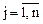 ).
).
Целевая функция для первой системы будет иметь вид:
 .
.
Для второй системы:
 .
.
Решив пару двойственных задач, можно определить выигрыш:
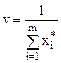
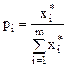
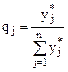 .
.
Процесс нахождения решения игры, с использованием методов линейного программирования включает следующие этапы:
1. Составляют пару двойственных задач линейного программирования, эквивалентных данной матричной игре.
2. Определяют оптимальные планы пары двойственных задач.
3. Используя соотношение между планами двойственных задач и оптимальными стратегиями и ценой игры.
Пример: Найти решение игры, определяемой матрицей:
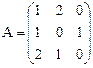
|
|
|
|
|
Дата добавления: 2014-12-27; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!