Способ 2. 5 страница

Решение.

Составим двойственные задачи линейного программирования.

Прямая задача.

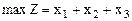
при

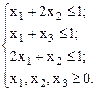
Двойственная задача:

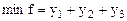
при

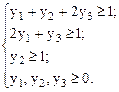
Решив задачи, получим: и . Следовательно цена игры: , а оптимальные стратегии игроков: и .

4.8. Задачи теории массового обслуживания. Классификация систем массового обслуживания

При исследовании операций очень часто приходится иметь дело с работой своеобразных систем, называемых системами массового обслуживания. Примерами таких систем могут быть билетные кассы, телефонные станции, магазины и т.д. Каждая система массового обслуживания состоит из некоторого числа обслуживающих единиц (приборов), которые мы будем называть каналами обслуживания. Каналами обслуживания могут быть линии связи, кассиры, продавцы и т.д. Системы массового обслуживания могут быть одноканальными и многоканальными.

Всякая система массового обслуживания предназначена для обслуживания какого-то потока заявок (требований), поступающие в какие-то случайные моменты времени. Обслуживание заявки продолжается некоторое случайное время 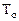, после чего канал освободится и готов к приему следующей заявки. Случайный характер потока заявок приводит к тому, что в некоторые моменты времени канал перегружен (заявок слишком много и поэтому они либо образуют очередь, либо покидают систему не обслуженной), в другие же периоды времени он либо работает с недостаточной загруженностью, либо совсем простаивает.

Предмет теории массового обслуживания – построение математических моделей, связывающих заданные условия работы системы (число каналов, их производительность, правила работы, характер потока заявок) с интересующими нас характеристиками – показателями эффективности систем массового обслуживания, описывающими, с той или другой точки зрения, ее способность справляться с потоком заявок. В качестве таких показателей могут применяться различные величины: среднее число заявок, обслуживаемых системой в единице времени; среднее число занятых каналов; среднее число заявок в очереди и среднее время ожидания обслуживания и т.д.

Системы массового значения делятся на типы по ряду признаков.

Классификация 1. Системы массового обслуживания с отказами или с очередью. В системах массового обслуживания с отказами заявка, поступившая в момент, когда все каналы заняты, покидает систему не обслуженной. Примеры таких систем: телефонная система. В системах массового обслуживания с очередью заявка, пришедшая в момент, когда все каналы заняты, не уходит, а становится в очередь и ожидает возможность быть обслуженной. Пример: магазин.

Классификация 1.1. Системы массового обслуживания с очередью делятся на разные виды, в зависимости от того, как организована очередь. Ограничения могут быть на длину очереди, на время ожидания ("системы массового обслуживания с нетерпеливыми заявками"). При анализе систем должна также учитываться и "дисциплина обслуживания": заявки могут обслуживаться в порядке поступления (первой пришла, первой обслуживается), либо в случайном порядке. Нередко встречается, так называемое обслуживание с приоритетом – некоторые заявки обслуживаются вне очереди. Приоритет может быть относительным (когда начатое обслуживание доводится до конца, а заявка с более высоким авторитетом имеет лишь право на лучшее место в очереди) и абсолютным (заявка с более высоким приоритетом вытесняет заявку с меньшим).

Классификация 2. Системы с многофазовым обслуживанием. Это системы, где обслуживание состоит из нескольких фаз.

Классификация 3. Открытие и закрытые системы массового обслуживания. В открытой системы массового обслуживания характеристики потока заявок не зависят ото того, в каком состоянии сама система. В замкнутой системе – зависят.

Оптимизация работы систем массового обслуживания может проводиться с точки зрения владельцев предприятия и обслуживаемых клиентов. С первой точки зрения желательно от предприятия получить максимальную прибыль при минимальны затратах, т.е. как организовать процесс, чтобы каналы по максимуму были заняты. Со второй точки зрения процесс нужно организовать так, чтобы было меньше очередей.

4.9. Потоки событий

Определение 1: Потоком событий называется последовательность событий, следующих одно за другим в какие-то случайные моменты времени.

Пример: Поток железнодорожных составов; поток вызовов на телефонную станцию; поток отказов компьютера и т.д.

Важной характеристикой потока событий является его интенсивность λ – среднее число событий, приходящееся на единицу времени. Интенсивность может быть постоянной или переменной, зависящей от времени.

Определение 2: Поток событий называется регулярным, если события следуют один за другим через определенные, равные промежутки времени, для нерегулярных потоков длительность промежутков – случайная величина.

Пример: Поток занятия в вузе, следующих с интервалом в 15 минут; поток пригородных автобусов, отправляющихся с вокзала каждый час (регулярные потоки). Поток отказов ЭВМ; поток заявок в службу скорой помощи (нерегулярные потоки).

Определение 3: Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени.

Пример: Поток запросов процессора к винчестеру (стационарный поток). Поток покупателей в магазин (нестационарный поток)

Определение 4: Поток событий называется потоком без последствий, если для любых двух непересекающихся участков времени и 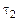число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой.

Пример: Поток пассажиров в метро (поток без последствий). Поток покупателей в магазине (поток с последствиями).

Определение 5: поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по нескольку сразу.

Пример: Поток клиентов в парикмахерской; поток поездов (ординарные потоки). Поток клиентов загса, направляющихся для регистрации брака; поток вагонов на станции (неординарные потоки).

Определение 6: Поток событий называется простейшим (или стационарным пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последствий.

Название "простейший" связано с тем, что процессы, связанные с простейшими потоками, имеют наиболее простое математическое описание. Простейший поток играет среди потоков особую роль. При наложении (суперпозиции) достаточно большого числа независимых, стационарных и ординарных потоков (сравнимых между собой по интенсивности) получается поток, близкий к простейшему.

Доказано, что для простейшего потока с интенсивностью λ интервал Т между соседними событиями имеет так называемое показательное распределение с плотностью

(t>0).

Величина λ в формуле называется параметром показательного закона. Для случайной величины Т, имеющей показательное распределение, математическое ожидание 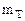есть величина, обратная параметру, а среднее квадратическое отклонение равно математическому ожиданию:

.

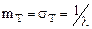Определение 7: Поток событий называется рекуррентным (поток Пальма), если он стационарен, ординарен, а интервалы времени между событиями представляют собой независимые случайные величины с одинаковым произвольным распределением.

Пример: Непрерывное обслуживание покупателей в магазине.

4.10. Схема гибели и размножения

Термин "схема гибели и размножения" ведет начало от биологических задач, где подобной схемой описывается изменение численности популяций.

Схема гибели и размножения очень часто встречается в теории массового обслуживания. Предположим, что все потоки событий, переводящие систему по стрелкам графа (рис. 17), – простейшие.

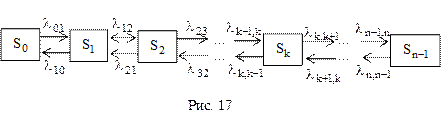
Пользуясь графом, представленным на рис. 17 составим и решим алгебраические уравнения для финальных вероятностей состояний. Для первого состояния имеем:

.

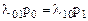Для второго состояния:

.

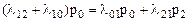Исходя из предыдущего равенства, получим:

;

далее, аналогично получим:

.

В общем случае:

.

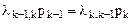где k принимает значения от 0 до n. Итак, финальные вероятности удовлетворяют уравнениям:

кроме того, необходимо учесть нормировочное условие:

.

Решим эту систему уравнений:

;

;

.

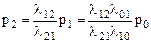В общем случае:

.

Обратим внимание на последнюю формулу: получили в числителе произведение интенсивностей, представленных на рис. 17 по верхним стрелкам, а в знаменателе произведение интенсивностей для нижних стрелок.

Подставим полученные равенства в нормировочное условие:

.

Отсюда:

.

4.11. Формула Литтла

Теперь мы выведем формулу, связывающую среднее число заявок 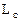, находящихся в системе массового обслуживания, и среднее время пребывания заявки в системе .

Рассмотрим произвольную систему массового обслуживания и связанные с нею два потока событий: поток заявок, прибывающих в систему, и поток заявок, покидающих систему. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в систему за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одинаковую интенсивность λ.

Обозначим: X(t) – число заявок, прибывших в систему массового обслуживания до момента времени t, Y(t) – число заявок, покинувших систему до момента t. И та и другая функции являются случайными и меняются скачком (увеличение или уменьшение на единицу). Очевидно, что для любого момента времени t их разность Z(t)=X(t)-Y(t) есть число заявок, находящихся в системе (Рис. 18). Рассмотрим большой промежуток времени Т и вычислим для него среднее число заявок, находящихся в системе:

.

Этот интеграл представляет собой площадь заштрихованной поверхности. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки. Обозначим эти времена Однако, под конец промежутка, некоторые прямоугольники войдут в заштрихованную систему не полностью, а частично, но при достаточно больших Т, этим обстоятельством можно пренебречь. Таким образом:

,

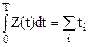где сумма распространяется на все заявки, пришедшие за время Т.

Разделим правую и левую части полученного равенства на Т и получим с учетом предыдущего:

,

Разделим и умножим правую часть полученной формулы на λ:

.

Величина λТ – среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен на среднее число заявок, то получим среднее время пребывания заявки в системе .

.

Отсюда:

.

Это и есть формула Литтла: для любой системы массового обслуживания, при любом характере потока заявок, при любом распределении потока обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок.

Точно таким же образом выводится и вторая формула Литтла, связывающая среднее время пребывания заявки в очереди 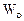и среднее число заявок в очереди :

.

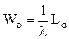4.12. Простейшие системы массового обслуживания

1. n-канальная система массового обслуживания с отказами (задача Эрланга ).

Это одна из первых задач теории массового обслуживания. Она возникла из нужд телефонии и была решена в начале 20 века датским ученым Эрлангом. Задача ставится так: имеется n каналов (линий связи), на который поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ (величина, обратная среднему времени обслуживания ). Найти финальные вероятности состояний системы массового обслуживания, а также характеристики ее эффективности:

А – абсолютную пропускную способность, т.е. среднее число заявок, обслуживаемых в единицу времени;

Q – относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;

– вероятность отказа, т.е. того, что заявка покинет систему необслуженной;

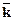– среднее число занятых каналов.

Решение.

Состояния системы S будем нумеровать по числу заявок, находящихся в системе (в данном случае оно совпадает с числом занятых каналов):

– в системе нет ни одной заявки, 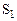– в системе находится одна заявка (один канал занят, остальные – свободны), …, – в системе находится k заявок (k каналов заняты, остальные свободны), …, – в системе находится n заявок (все каналы заняты). Граф состояний системы массового обслуживания представлен на рис. 19.

Воспользуемся уже готовыми формулами для финальных вероятностей в схеме гибели и размножения. Получим:

Обозначим отношение λ к μ через ρ:

.

Тогда:

.

Последняя формула называется формулой Эрланга.

Исходя из полученной формулы, найдем все остальные характеристики системы массового обслуживания:

.

Отсюда найдем относительную пропускную способность – вероятность того, что заявка будет обслужена:

.

Абсолютную пропускную способность получим, умножая интенсивность потока заявок на λ на Q:

Среднее число занятых каналов можно рассчитать по следующей формуле:

.

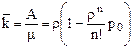Дата добавления: 2014-12-27