Дисперсионный анализ. Основной целью дисперсионного анализа является исследование значимости различия между средними

Основной целью дисперсионного анализа является исследование значимости различия между средними. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений). Откуда произошло название Дисперсионный анализ? Может показаться странным, что процедура сравнения средних называется дисперсионным анализом. В действительности, это связано с тем, что при исследовании статистической значимости различия между средними двух (или нескольких) групп, мы на самом деле сравниваем (т.е. анализируем) выборочные дисперсии. Фундаментальная концепция дисперсионного анализа предложена Фишером в 1920 году. Возможно, более естественным был бы термин анализ суммы квадратов или анализ вариации, но в силу традиции употребляется термин дисперсионный анализ.

Дисперсионный анализ проводится за некоторыми общими схемами, которые мы рассмотрим на примере однофакторного дисперсионного анализа.

1). Первичные данные, которые подлежат дисперсионному анализу, группируют в виде корреляционной таблицы, в которой градации организованного (регулируемого) фактора А обычно располагают по горизонтали в верхней части таблицы, а числовые значения признака X, то есть варианты Хi, размещают соответственно по градациям фактора А.

В таблице: r - количество градаций фактора А.

Таблица 5. Корреляционная таблица.

№ опыта	Уровень фактора А
А;	А2	А,	...	Аг
	Х11	X12	X13	...	X1г
	X21	X22	Х23	...	X2r
	X31	X32	X33	...	X3г
...	...	...	...	...	...
L	ХL1	XL2	XL3		XLг
Групп. Сред.			...	...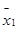

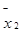
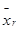
2) Сгруппировав выборочный материал в таблицу, находят средние величины: среднюю арифметическую всего комплекса, так наз. общую среднюю Хобщ и групповые средние х, - по градациям фактора А:

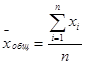
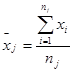
где п- общее количество опытов, n_j – количество опытов по каждой из градаций. Если количество испытаний в градациях одинаково, то n_j = L.

3) Определяют общую сумму квадратов отклонений Су, равную сумме квадратов отклонений всех значений случайной величины от общей средней, то есть:

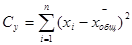
4) Определяют сумму квадратов отклонений по организованным факторам, с учетом статистического веса групповых средних (характеризует рассеивание между группами). При одинаковом числе вариант в градациях комплекса эта сумма

,

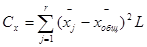если L постоянно для всех опытов. При разных количествах вариант –

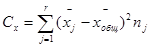
5) Вычисляют сумму квадратов отклонений по случайным факторам (характеризует рассеивание в группах):

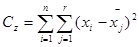
Практически остаточную сумму находят по формуле:

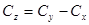
6). Определив сумму квадратов отклонений, устанавливают число степеней свободы, которые могут быть равны:

для общей дисперсии k_y = n - 1

для факторной k_x = r - 1

для случайной (остаточной) k_z = n - r

7) Отношением сумм квадратов отклонений к соответствующему числу степеней свободы определяются дисперсии:

общая: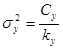

факторная: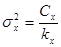

случайная (остаточная)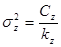

Если 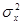> , то делаем предварительный вывод о том, что фактор имеет влияние; если 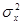< ,то фактор не оказывает существенного влияния.

8) Для установления значимости вывода о влиянии регулируемого фактора на результативный признак используют критерий Фишера - Cнедекора, в виде отношения факторной дисперсии к дисперсии случайной (остаточной):

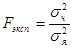
9) Заключительным этапом дисперсионного анализа является сравнение фактической величины критерия F_эксп с его стандартным значением F (а;k_z; k_x) найденным по Таблице 1 Приложений для уровня значимости а изначениям степеней свободы k_z и k_x.

Если Fэ ксп >F, - делают вывод о статистической значимости влияния на результат исследования организованных факторов, если Fэ ксп <F, то такой вывод делать нельзя.

В пакете Статистика для проведения дисперсионного анализа используется модуль ANOVA/MANOVA (Analysis of variance в случае однофакторного анализа и Multiply analysis of variance в случае многофакторного).

Дата добавления: 2014-12-27