Определение требуемого числа наблюдений в выборках для получения значимого различия показателя в двух выборках

Полученное расчетное значение критерия Стьюдента следует сравнить с табличным, определенным для данного числа степеней свободы, при заданном уровне значимости, который обычно равен или менее 0.05. Вывод о том, что различие показателя в сравниваемых парах связанных выборок значимо, можно сделать, если табличное значение критерия Стьюдента меньше рассчитанного исследователем.

Связанными (или зависимыми) называют выборки, состоящие из одних и тех же объектов, наблюдающихся в различных условиях, например, до некоторого воздействия и после него, или в период разгара заболевания, на 3, 9 и т.д. дни лечения.

Независимыми (несвязанными) называются выборки, в каждой из которых наблюдаются различные объекты, например, первая, контрольная группа, принимающая плацебо, и вторая, опытная, получающая определенный препарат.

Оценка значимости различия показателей в связанных выборках.

Проверка статистических гипотез по результатам выборочного наблюдения.

Теория проверки статистических гипотез является основным инструментом доказательной медицины. Доказа́тельная медици́на (англ. Evidence-based medicine — медицина, основанная на доказательствах) — термин описывает такой подход к медицинской практике, при котором решения о применении профилактических, диагностических и лечебных мероприятий принимаются исходя из полученных доказательств их эффективности и безопасности, и предполагающий поиск, сравнение, обобщение и широкое распространение полученных доказательств для использования в интересах больных

При сравнении показателей, например, в контрольной (прием плацебо) и опытной (прием настоящего препарата) группах выдвигают статистические гипотезы:

Н1 – о существенном различии показателя в опытной и контрольной группах;

Н0- нулевую гипотезу – о равенстве (отсутствии различий) показателя в опытной и контрольной группах.

Гипотезу Н1 принимают, если ее вероятность имеет значение равное или больше 95% и отклоняют, если ее вероятность будет меньше 95%. В этом случае принимают гипотезу Н0, а ее вероятность, как альтернативной, будет р>0.05.

Вероятность Н0 р называют уровнем значимости, а величину 1-р называют доверительной вероятностью гипотезы Н1 (альтернативной). Статистическая значимость результата – это мера уверенности в его "истинности". Вопрос, который необходимо при этом задавать: "Насколько можно доверять этому результату?". Представьте, что мы проводили исследование на основе только двух пациентов. Конечно же, в этом случае к результатам нужно относиться с опасением. Если же были обследовано большое количество больных, то сделанным выводам уже можно доверять. Степень доверия и определяется значением p-уровня.

Более высокий p- уровень соответствует более низкому уровню доверия к результатам, полученным при анализе выборки. Например, p- уровень, равный 0.05 (5%) показывает, что сделанный при анализе некоторой группы вывод является лишь случайной особенностью этих объектов с вероятностью только 5%.

Другими словами, с очень большой вероятностью (95%) вывод можно распространить на все объекты.

Во многих исследованиях 5% рассматривается как приемлемое значение p-уровня. Это значит, что если, например, p = 0.01, то результатам доверять можно, а если p=0.06, то нельзя.

По 95% -м доверительным интервалам дается приближенное графическое решение. Если доверительные интервалы не перекрывают друг друга или их перекрытие не превышает 1/3, можно считать, что имеется значимое различие средних значений показателей в двух выборках. Если перекрытие доверительных интервалов превышает 1/3, следует признать, что различие средних значений показателя в этих двух выборках незначимое, недостоверное. Однако, приближенный метод оценки значимости различия по доверительным интервалам может использоваться в качестве экспресс-метода, он хорош для графической демонстрации средних значений признаков и 95% - х доверительных интервалов их истинных значений. Более обоснованное решение получают с применением критерия Стьюдента.

Надежные значения критерия можно получить по формуле:

Исходными данными для решения служат числовые характеристики разностей показателя, получаемые по исходной матрице наблюдений. Расчет критерия Стьюдента проводится по формуле:

где 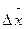- средняя разность показателя в сравниваемых группах;

- средняя квадратичная ошибка средней разности показателей;

, где - среднее квадратичное отклонение разности показателей.

Величина t–критерия значимости различия р зависит от разности , 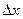и числа наблюдений в выборках n₁,n₂.

При небольших объемах выборки увеличиваются средние квадратичные ошибки и уменьшается величина t-критерия, а следовательно уменьшается вероятность гипотезы Н1 о различии, увеличивается вероятность гипотезы Н0 о соответствии показателя в сравниваемых выборках. При желании исследователя получить значимое различие показателя следует увеличивать число наблюдений в выборках. Так, при заданном уровне значимости р=0.05 требуемое число наблюдений должно удовлетворять следующим требованиям:

-при сравнении независимых выборок 1 и 2

и ;

- при сравнении связанных выборок

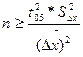
Дата добавления: 2014-12-27