Как видим, ошибка уменьшается с увеличением объема выборки. Так, чтобы уменьшить ошибку в два раза, число наблюдений надо увеличить в четыре раза

Числовые характеристики переменных, рассчитанные по выборкам, содержат ошибки по отношению к аналогичным в ГС. Характеристикой ошибок, следующих нормальному распределению, является средняя квадратичная ошибка.

Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс обозначает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение. Иными словами, эксцесс определяет наличие выбросов в значениях.

Асимметрия характеризует степень несимметричности распределения относительно его среднего. Положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.

Доверительный интервал для некоторой величины - это диапазон вокруг значения величины, в котором находится истинное значение этой величины (с определенным уровнем доверия).

Вид распределения характеризуют коэффициенты:

- асимметрии в натуральном и стандартизованном виде As

- эксцесса в натуральном и стандартизованном виде Es.

По числовым характеристикам судят о соответствии эмпирического распределения теоретическому нормальному распределению. Его можно оценить как близкое к нормальному, если:

- среднее арифметическое, геометрическое и гармоническое значения незначительно различаются друг от друга, а также с модой и медианой;

- минимальные и максимальные значения примерно равноудалены от среднего значения;

- стандартизованные коэффициенты асимметрии и эксцесса по абсолютной величине меньше |2|.

Любое исследование должно включать элемент оценки точности и надежности числовых характеристик. Оценкой точности и надежности является 95% доверительный интервал истинного среднего значения. Например, истинное среднее значение ГС находится в доверительном интервале

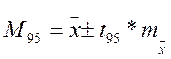
где t₉₅ - табличное значение t –критерия Стьюдента, отвечающее доверительной вероятности 95% по числу степеней свободы df= n-1, n – количество наблюдений;

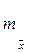- средняя квадратичная ошибка среднего значения, определяемая по формуле

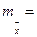
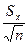
где Sx – среднее квадратичное отклонение показателя в выборке.

Sx= , .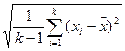

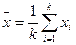В ряде случаев целесообразно определять 95% доверительный интервал для возможных значений показателя.

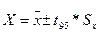
Эмпирическое распределение переменной представляется в виде статистического ряда распределения, характеризующего связь между возможными значениями переменной и относительной частотой их наблюдения в выборке. Для построения статистического ряда распределения в выборке необходимо иметь несколько десятков и более наблюдений, которые группируются в виде интервалов (разрядов).

Выбор числа интервалов группировки возможен:

- по формуле Стерджеса:

m=1+3,32xlgn,

- по эмпирически выработанным рекомендациям:

Объем выборки, n	Число интервалов, m
25 - 40	5 - 6
40 - 60	6 - 8
60 - 100	7 - 10
100 - 200	8 - 12
Более 200	10 -15

Подготовку данных для статистического ряда распределения выполняют в следующем порядке:

- в зависимости от числа наблюдений n выбирают число интервалов ряда m;

- определяют размах вариационного ряда Р=Хмах-Хмин;

- рассчитывают длину интервала L=Р/m;

- определяют границы и средние точки интервалов;

- подсчитывают частоту наблюдений и накопленную частоту для каждого интервала.

По данным статистического ряда распределения строят гистограмму и кумулятивную линию распределения, или линию тренда. По виду гистограммы и линии делают предварительные выводы о характере и соответствии эмпирического распределения определенному теоретическому распределению.

Закон нормального распределения случайной переменной .

Дата добавления: 2014-12-27