Виды средних арифметических величин

Сущность и значение средних величин.

Различие между индивидуальными явлениями – это вариации. Среди массовых явлений мы выделяем характерное или среднее. Средние расценки, средние показатели… это нам знакомо.

Главное значение средних величин – их обобщающая функция. Множество различных индивидуальных значений заменяются средней величиной, характеризующей всю совокупность явлений.

Средняя величина – это обобщающая характеристика однородной совокупности явлений по определенному признаку.

Например, индивидуальная выработка у пяти рабочих за месяц составила 135, 141, 153, 159, 162 детали. Чтобы получить среднюю выработку на одного рабочего в месяц, нужно сложить эти показатели и ∑ (сумму) разделить на 5.

_

Х = 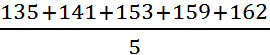= =150(дет.)

Средние величины широко применятся в статистике (в учебнике прочтите об этом стр. 66-80).

Средняя арифметическая величина бывают простой и взвешенной.

а) Простая средняя величина – сумма всех индивидуальных величин одного вида, деления на их число.

Х1,Х2,Х3, …….Хn – индивидуальное значение признака;

n - число индивидуальных величин;

_

Х – средняя величина;

_

∑ - сумма, Х = ∑ Xi/n

Или средняя арифметическая простая равна частному от деления суммы индивидуальных значений признака на их количество.

Эта величина применяется: средняя продолжительность жизни, средняя заработная плата по отрасли, предприятию и т.д.

Б) Средняя арифметическая взвешенная (х1,х2 – индивидуальные значения признака, варианта- мы знаем) f1,f2,f3,…fn – числа, показывающие, сколько ряд повторяется варианта или частоты;

X = =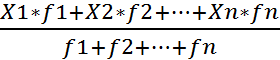

Средняя арифметическая взвешенная равна сумме произведений вариант (х) на их частоты или веса (f), деленной на сумму частот (весов) f.

_

Х =

7.3. Свойства средней арифметической величины:

1.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин:

Если Xi = Yi+Zi, то

_ _ _

X = 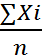= = 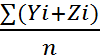=Y+ Z

Правило показывает, в каких случаях можно суммировать средние величины.

Н-р, выпускаемые изделия состоят из 2-х деталей Y и Z и на изготовление каждой из

_ _

них расходуются в среднем Y-3часа; Z = 5 часов, то средние затраты времени на

_

изготовление одного изделия(X) =: 3+5=8

_ _ _

часов., т.е..(X=Y+Z);

2. Алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, т.к. сумма отклонений в одну сторону полагается _ суммой отклонений в другую сторону, т.е.

_

∑(X-X) = 0, потому что

_ _ _

∑(X-X) = ∑X - ∑X = ∑X-nX=∑x-n ;

Это правило показывает, что средняя является равнодействующей.

3.Если варианты ряда уменьшить или увеличить на одно и то же число а, то средняя уменьшится или увеличится на это же число а:

_

Х= ±a;

4.Если все частоты ряда разделить или умножить на одного и то же число d, то средняя не изменится:

_

X=

Свойствo показывает, что средняя зависит не от размеров весов, а от соотношения между ними. Следовательно в качестве весов могут выступать не только абсолютные, но и относительные величины структуры.

Дата добавления: 2014-12-27