Другие виды средних величин

а) Средняя гармоническая.

Как мы определяем среднюю арифметическую?

У нас есть ряд вариантов и частот, т.е. значение Х и f

Иногда известны индивидуальные значения признака Х и произведение Хf, а частоты f неизвестны.

Для расчета средней обозначим произведение Z=fХ,

f= Теперь по имеющимся данным X и Z рассчитаем среднею, f выражаем через X и Z;

_ _

X= = (=0)

Средняя в такой форме называется средней _ гармонической взвешенной и обозначается 0.

Следовательно, средняя гармоническая тождественна средней арифметической. Она применяется тогда, неизвестны веса f, а известно произведение fX=Z

Когда fX одинаковы или равны единице (Z=1), применяется средняя гармоническая простая:

_

Xгарм.= = = 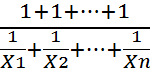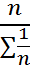, где

х – отдельные варианты;

n – число вариантов.

б) Средняя геометрическая.

Если имеется n коэффициентов роста, то формула среднего коэффициента роста имеет вид:

_

К = .

Средняя геометрическая равна корню степени n из произведения из произведения коэффициентов роста, характеризующих отношение величины каждого последуещего периода к величине предыдущего.

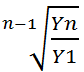К= , т.к ;

n- число лет; y-это средний коэффициент роста.

Вычисление средней геометрической связано с извлечением корней, а это можно сделать при помощи таблицы логарифмов.

_

К= 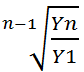, а lg K= :(n-1).

в) Средняя квадратическая.

Часто необходимо вычислить среднюю, выраженную в виде квадратных функций. Н-р, средние диаметры труб, колёс, стволов, средние стороны квадратов. Для этого применяется средняя квадратическая:

1) средняя квадратическая простая рассчитывается путем извлечения квадратного корня из частного от деление суммы квадратов отдельных значений признака на их число:

_

X= = ;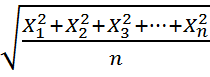

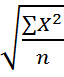2) средняя квадратическая взвешенная равна:

_

X= , где

f- веса.

Задача.

Пять рабочих выработали соответственно: 20,16,22,28,14, деталей.

Определить:

1) Среднюю арифметическую:

_

Хар= = (деталей)

2) Среднюю гармоническую:

_

Xгарм= =18,8(дет)

3) Средняя геометрическую:

_

Xгеом= = = =19,4(дет.)

4) Средняя квадратическую:

_

Xкв.= = =21,2(дет)

7.5. Структурные средние. Мода и медиана.

Для характеристики величины варьирующего признака пользуется структурными средними - модой и медианой.

Мода – наиболее часто встречающееся значение ряда.

Пример: при определение размера одежды, обуви, наиболее распространенной цены на определенный товар…

При расчете моды для интервального вариационного ряда необходимо вначале определить модальный интервал, а затем значение модальной величины признака.

Мода рассчитывается по формуле:

= , где

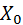- нижняя граница модального интервала;

h- величина модального интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

-частота интервала, следующего за модальным.

Но мода и средняя величина по-разному характеризуют совокупность. Мода определяет непосредственно размер признака, свойственный, хотя и значительной части, но не всей совокупности.

Медиана - значения элемента, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения, она делит ряд на две равные части.

При нахождении медианы интервального вариационного ряда вначале определяют медиальный интервал, в пределах которого находится медиана, а затем- приближенное значение медианы по формуле:

= , где

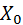- нижняя граница интервала, который содержит медиану;

h- величина медиального интервала;

∑f- сумма частот или членов ряда;

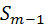? - сумма накопленных частот интервалов, предшествующих медианному;

- частота медиального интервала.

7.6. Показатели вариации.

Когда мы характеризуем любое общественное явление, то статистика включает большое число вариаций, т.е. признаков, характеризующих это явление. Н-р, З/п- её величина зависит от: специальности, разряда, стажа, образования… от состояния здоровья и.т.д.

При характеристике изменчивости признака какой-то совокупности применяется система абсолютных и относительных показателей:

I) Абсолютные показатели вариации:

_

1) Среднее линейное отклонение d - это средняя величина из абсолютных значений отклонений отдельных вариант от их средней.

а) Среднее линейное отклонение рассчитывается по формуле средней арифметической простой;

_ _

d= ;

б) По средней арифметической взвешенной:

_ _

d= ;

(G греч. буква сигма)

1) Дисперация 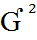- это средний квадрат отклонений индивидуальных значений признака от их средний величины

_

= ;

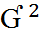При равенстве весов или когда они равны 1.

_

= ;

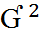3) Среднеквадратическое отклонение равно корню квадратному из суммы квадратов отклонений индивидуальных значений признака от их средней, т.е из дисперсии.

1. Тема № 8: Виды и формы взаимосвязей между явлениями.

Все явления общественной жизни взаимосвязаны и взаимообусловлены. Как выявить и измерить взаимосвязи между изученными явлениями?

Связующие признаки подразделяются:

а) факторные - эти показатели воздействуют и изменяют другие показатели, зависящие от них.

б) результативные – то, что получается в итоги изучения, вычисления.

Типы связей между явлениями:

1) Функциональные вязи - определенному значению факторного признака ответствует строго определенное значение результативного признака. Т.е. такая связь 2-х величин возможна, если вторая зависит только от первой и ничего больше. В реальной природе и обществе таких связей нет. Их придумали для упрощения анализа явлений (мы говорим: абстрагируясь от всего остального, мы допускаем, что…). Такие науки как механика, электроника, акустика, экономика успешно используют функциональные связи в аналитических и прогностических целях. Например, длина года (период обращения земли вокруг солнца) почти функционально зависит только от массы Солнца и расстояния Земли от него.

2) Статистические связи – одному и тому же значению признака может соответствовать несколько значений результативного признака; эти связи проявляются в массе случав и при том – в среднем.

Сравнивая показатели урожайности ряда лет, делаем выводы:

· урожайность колеблется;

· рост урожайности наблюдается лишь в среднем, как тенденция.

Тенденция динамики связана с действием долговременно существующих причин и условий развития процесса.

Колебания связаны с действием краткосрочных или циклических факторов, влияющие на отдельные уровни динамического ряда, и отклоняющих уровни от тенденции то в одном, то в другом направлении.

При статистическом изучении динамики нужно четко разделить два основных элемента:

1) тенденцию;

2) колеблемость.

Тенденцию и колебания показывает наш график «Динамика урожайности картофеля».

По оси абцисс всегда отражается время, по оси ординат – уровни. По обеим осям строго соблюдается масштаб, иначе характер динамики будет искажен.

Дата добавления: 2014-12-27