What is the Newton-Raphson method and how does it differ from other methods to solve nonlinear equations?

Места, где надо делать сужду в Коране.

Пауза.

Сакта.

Правило чтения соединения некоторых слов.

Когда за танвинным окончанием следует буква с сукуном, возникает необходимость введения в танвинное окончание дополнительной огласовки (кясра).

لُمَزَةٍ نِ الَّذِي

مُحَمَّدًا نِ الْوَسَيلَةَ

مَحْمُودًا نِ الَّذِى

В Коране при чтении в четырех местах делается краткая пауза звука и дыхания одновременно, которая называется (сакта), после чего сразу же продолжается чтение. Это между словами:

1) 18 сура «Пещера» (كهف) аят (1) عِوَجًا ^سقَيِّمًا

2) 36 сура «Йасин» (يس) аят (52) مِنْ مَرْقَدِنَا ^سهَذَا

3) 75 сура «Воскресение» (قيامة) аят (27) مَنْ ^سرَاقٍ

4) 83 сура «Обвешивание» (مطففين) аят (14) بَلْ ^سرَانَ

При паузе, слова могут заканчиваться в трех вариантах: с сукуном, на фатхIу, или букву (هْ) с сукуном.

يَعْلَمُونْ – يَعْلَمُونَ	يُؤْمِنُونْ – يُؤْمِنُونَ	نَسْتَعِينْ – نَسْتَعِينُ
حَامِيَهْ – حَامِيَةٌ	تَوَّابَا – تَوَّابًا	يُسْرَا – يُسْرًا

1) В суре اَلْأَعْرَافُ в конце 206-ого аята (وَلَهُ يَسْجُدُونَ)

2) В суре الرَّعْدُ в конце 45-ого аята (وَظِلَالُهُمْ بِالْغُدُوِّ وَالْاَصَالْ)

3) В суре النَّحْلُ в конце 19-ого аята (وَهُمْ لَا يَسْتَكْبِرُونَ)

4) В суре اَلْإِسْرَاءُ в конце 107-ого аята (يَخِرُّونَ لِلْاَذْقَانِ سُجَّدَا)

5) В суре مَرْيَمً в конце 57-ого аята (خَرُّوا سُجَّدًا وَبُكِيًّا)

6) В суре اَلْحَجُّ в конце 18-ого аята (إِنَّ اللهَ يَفْعَلُ مَا يَشَاءُ)

7) В суре اَلْفُرْقَانُ в конце 60-ого аята (وَزَادَهُمْ نُفُورَا)

8) В суре النَّحْلُ в конце 25-ого аята (وَيَعْلَمُ مَا تُخْفُونَ وَمَاتُعْلِنُونَ)

9) В суре السَّجْدَةُ в конце 15-ого аята (وَهُمْ لَا يَسْتَكْبِرُونَ)

10) В суре ص в конце 24-ого аята (وَخَرَّ رَاكِعًا وَأَنَابَ)

11) В суре فُصِّلَتْ в конце 37-ого аята (إِنْ كُنْتُمْ إِيَّاهُ تَعْبُدُونَ)

12) В суре النَّجْمُ в конце 62-ого аята (فَاسْجُدُوا لِلَّهِ وَاعْبُدُوهُ)

13) В суре الاِنْشِقَاقُ в конце 21-ого аята (وَ إِذَا قُرِئَ عَلَيْهِمُ الْقُرْآنُ لَا يَسْجُدُونَ)

14) В суре العَلَقُ в конце 19-ого аята (وَاسْجُدْ وَاقْتَرِب)

Methods such as bisection method and the false position method of finding roots of a nonlinear equation f(x=0 require bracketing of the root by two guesses. Such methods are called bracketing methods. These methods are always convergent since they are based on reducing the interval between the two guesses to zero in on the root.

In the Newton-Raphson method, the root is not bracketed. Only one initial guess of the root is needed to get the iterative process started to find the root of an equation. Hence, the method falls in the category of open methods.

Newton-Raphson method is based on the principle that if the initial guess of the root of f(x)=0 is at x_i, then if one draws the tangent to the curve at f(x_i), the point x_i+1 where the tangent crosses the x -axis is an improved estimate of the root (Figure 1).

Using the definition of the slope of a function, at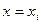

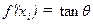
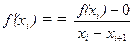
which gives

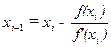(1)

Equation (1) is called the Newton-Raphson formula for solving nonlinear equations of the form 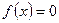. So starting with an initial guess, x_i, one can find the next guess, x_{i +1}, by using equation (1). One can repeat this process until one finds the root within a desirable tolerance.

Дата добавления: 2014-12-27